 |
#1 - 28-05-2014 19:00:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 28-05-2014 22:58:45
- NickBern
- Passionné de Prise2Tete
- Enigmes résolues : 45
- Messages : 50
âteau 78
Je lui proposerai de plier la nappe en deux, et de poser les deux merveilles dessus.
Ainsi les 9 tâches sont bien "cachées " "sous" les deux gâteaux !!

Note : il peut aussi retourner la nappe ça va sans dire..
#3 - 29-05-2014 05:05:49
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteau 7
Mais cela ne dépend t-il pas (aussi) des dimensions relatives de la nappe par rapport aux gâteaux triangulaires ? Ou n'ai-je (encore une fois) rien compris ?
#4 - 29-05-2014 10:31:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 78
La forme de la table n'a pas d'importance , on peut supposer qu'elle est très grande par rapport aux gâteaux .
Vasimolo
#5 - 29-05-2014 10:40:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 788
Je ne dois pas bien comprendre le problème: au pire, un triangle ne pourrait recouvrir qu'une seule tàche, si les tàches sont suffisamment éloignées les unes des autres. Il y a donc bien un rapport cadre/ triangle à respecter, mais tu n'en parles pas....
#6 - 29-05-2014 11:43:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 87
Ce qu'il faut voir Nodgim c'est que neuf taches prises au hasard peuvent toujours être cachées par les deux gâteaux astucieusement disposés . Même si la table est immense les taches sont plutôt groupées .
Vasimolo
#7 - 29-05-2014 13:48:03
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 778
Si je me ramène à un problème en 1 dimension, avec des taches alignées et 2 segments pour les recouvrir, alors si 3 tâches prises au hasard peuvent toujours être recouvertes par les 2 segments, on peut en conclure facilement que l'ensemble des tâches seront toujours recouvertes par ces 2 segments.
Le problème posé étant en 2d, je suppose que le "raisonnement" est le même, et que donc 3²=9 tâches prises au hasard pouvant être recouvertes on pourra toujours recouvrir l'ensemble des tâches par les 2 gâteaux.
(Et il en irait de même pour des tâches en 3d englobéestétraèdrées dans des tétraèdres pour peu que 3^3=27 tâches prises au hasard peuvent être entétraèdrées)
Ceci n'est pas du tout une démonstration mais je vais essayer de démarrer la dessus...
#8 - 29-05-2014 14:27:57
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gtâeau 78
Bonjour 
Pourquoi 9, il me semble que ça marche aussi avec 2.
Pour une fois j'ai une explication simple :
Faisons un raisonnement par récurrence :
Si il n' y a que 9 taches sur la table, alors on peut trivialement recouvrir les 9 taches.
Maintenant supposons que l'on peut toujours recouvrir n+9 taches.
Montrons que l'on peut alors en recouvrir n+10.
Donc si j'ai n+10 taches, j'utilise mon hypothèse de récurrence pour en recouvrir n+9.
Imaginons que le dessous des gâteaux est imbibé d'encre. Je fais tous les déplacements possibles des gâteaux (en les faisant glisser sur la table) avec la contrainte de toujours recouvrir ces n+9 taches. "L'encre imaginaire" sous les gâteaux a dessiné une région sur la table (pas forcément connexe). On a deux cas :
Soit la n+10 ième tache est dans cette région, alors je peux déplacer les gâteaux de manière à recouvrir cette dernière tache tout en recouvrant toujours les n+9 autres.
Soit la n+10 ième tache est hors de cette région et alors dans ce cas l'ensemble des 9 taches formé de cette n+10 ième tache et de huit autres taches ne peut pas être recouvert par un gâteau, ce qui contredit l'affirmation du pâtissier.
Donc par récurrence, on pourra toujours recouvrir toutes les taches.
Il me semble que ce raisonnement fonctionne aussi en remplaçant 9 par 2 (et 10 par 3), non ?
Il y a sûrement plus simple.
#9 - 29-05-2014 19:34:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteeau 78
@Golgot : bonne idée mais la deuxième dimension ajoute quelques difficultés .
@Cogito : la tache que tu traces avec tes déplacements n'est pas une vrai tache 
Vasimolo
#10 - 29-05-2014 20:08:53
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâtea 78
Avec mes déplacement je ne trace pas une tache, ce que je trace c'est une zone qui a la propriété que quelque soit la position du triangle dans cette zone, il recouvre toujours les mêmes taches (parmi le groupe de taches qu'il recouvrait dans le recouvrement des n+9 taches). Je ne sais pas si je m'exprime bien  . .
Par exemple si A est un ensemble de taches recouvertes par le triangle, alors ce que je trace c'est la zone maximale où quelque soit la position du triangle dans cette zone, il recouvre toujours les taches de l'ensemble A.
Donc si une tache t n'appartient pas à cette zone, alors je ne pourrais pas recouvrir avec mon triangle les taches de l'ensemble (A union {t}).
Ici on a deux triangles, donc des zones comme décrites ci-dessus il y en a deux.
Dans ma démonstration j'ai dit que c'était une seule zone pas forcément connexe, mais ça ne change pas le raisonnement.
EDIT :
Cependant, ma conclusion est un peu hâtive, effectivement 
Il y a sûrement plus simple.
#11 - 29-05-2014 22:12:11
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâteeau 78
En faite si on appelle Z1 la zone du premier triangle, et Z2 la zone du deuxième triangle, et t la n+10 ième tache qui n'est pas dans l'union de Z1 et Z2 alors on a deux cas.
cas 1 :
Soit le premier triangle va recouvrir la tache t, il découvrira alors un ensemble de taches que l'on va appeler A1.
cas 2 :
Soit le second triangle va recouvrir la tache t, il découvrira alors un ensemble de taches que l'on va appeler A2.
Si A1 est inclus dans Z2 ou A2 est inclus dans Z1 alors on n'a pas de problème.
Sinon,
i) il existe une tache p1 de A1 qui n'est pas dans Z2.
ii) il existe une tache p2 de A2 qui n'est pas dans Z1.
Maintenant, on va déplacer le premier triangle pour qu'il recouvre t (ainsi il découvre les taches de A1, dont p1).
On va déplacer le deuxième triangle pour qu'il recouvre les taches de A1 (dont p1), comme A1 n'est pas inclus dan Z2, il va découvrir un en semble de taches que l'on va appeler B2.
Le premier triangle contiens un nouvelle ensemble de tache pour lequel on a une nouvelle zone que nous appellerons NZ1. Si B2 est inclus dans NZ1 alors il n' y a pas de problème.
En échangeant les rôles du premier et second triangles, on peut définir également un ensemble de taches B1 et une nouvelles zones NZ2 telle que si B1 est inclus dans NZ2 alors on n'a pas de problème.
Sinon,
iii) il existe q1 une tache de B1 qui n'est pas dans NZ2.
iv) il existe q2 une tache de B2 qui n'est pas dans NZ1.
Maintenant montrons que les points t, p1, p2, q1, et q2 ne peuvent pas être recouverts par les deux triangles.
a) Si le premier triangle recouvre t, alors il ne recouvre pas p1 et il ne recouvre pas q2 non plus (qui n'est pas dans la nouvelle zone NZ1).
-Si le deuxième triangle recouvre p1 alors il ne recouvre pas q2 et vice versa.
b) Si le deuxième triangle recouvre t, alors il ne recouvre pas p2 et il ne recouvre pas q1 non plus.
-Si le premier triangle recouvre p2 alors il ne recouvre pas q1 et vice versa.
Donc tout ensemble de 9 points contenant t,p1,p2,q1,q2 ne peut être recouvert par les deux triangles.
Donc en fait cette propriété est vraie à partir de 5.
C'est long à expliquer, mais si on arrive à visualiser, c'est pas trop compliquer 
Il y a sûrement plus simple.
#12 - 31-05-2014 08:53:13
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
gâteay 78
ça ne marche pas avec seulement 6 pts ?
#13 - 31-05-2014 09:18:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Gâetau 78
Je pense que le problème marche dès 5 taches.
Raisonnement par l'absurde :
Je ne peux pas recouvrir une des taches, pourquoi ?

Parce que la mobilité de chacun de mes deux triangles en direction de cette tache est limitée par un ou deux taches (une rouge et deux violettes)
Conclusion : en choisissant ces trois taches et la verte, je ne peux déjà pas recouvrir un groupe de 4 taches au hasard ce qui va à l'encontre de l'énoncé.
#14 - 31-05-2014 09:38:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtzau 78
9 , 8 , 7 , 6 , 5 , ... taches .
Avant de chercher une démonstration on peut essayer de donner un exemple de cinq taches qui ne peuvent pas être recouvertes par deux triangles alors que quatre quelconques d'entre elles le peuvent . Ou six taches ne pouvant pas être recouvertes alors que cinq d'entre elles ...
En fait je n'ai pas trop d'idée sur la limite , je sais simplement que ça marche avec neuf points .
Avis aux amateurs 
Vasimolo
#15 - 31-05-2014 10:01:56
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gââteau 78
Pour un triangle seul, avec une orientation donnée, si 3 pts quelconques sont recouvrables, alors tous le sont; ça marche d'ailleurs avec n'importe quelle figure convexe.
C'est assez facile à montrer: on prend un coté de la figure, on dira qu'il est horizontal en bas du plan. La figure ne peut monter au dela du point le plus bas, ensuite elle ne peut que translater à droite ou à gauche de part et d'autre de ce pt. Si elle recouvre les 2 pts extêmes à droite et à gauche, alors elle recouvre tous les pts.
#16 - 31-05-2014 10:19:57
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Gâteau 788
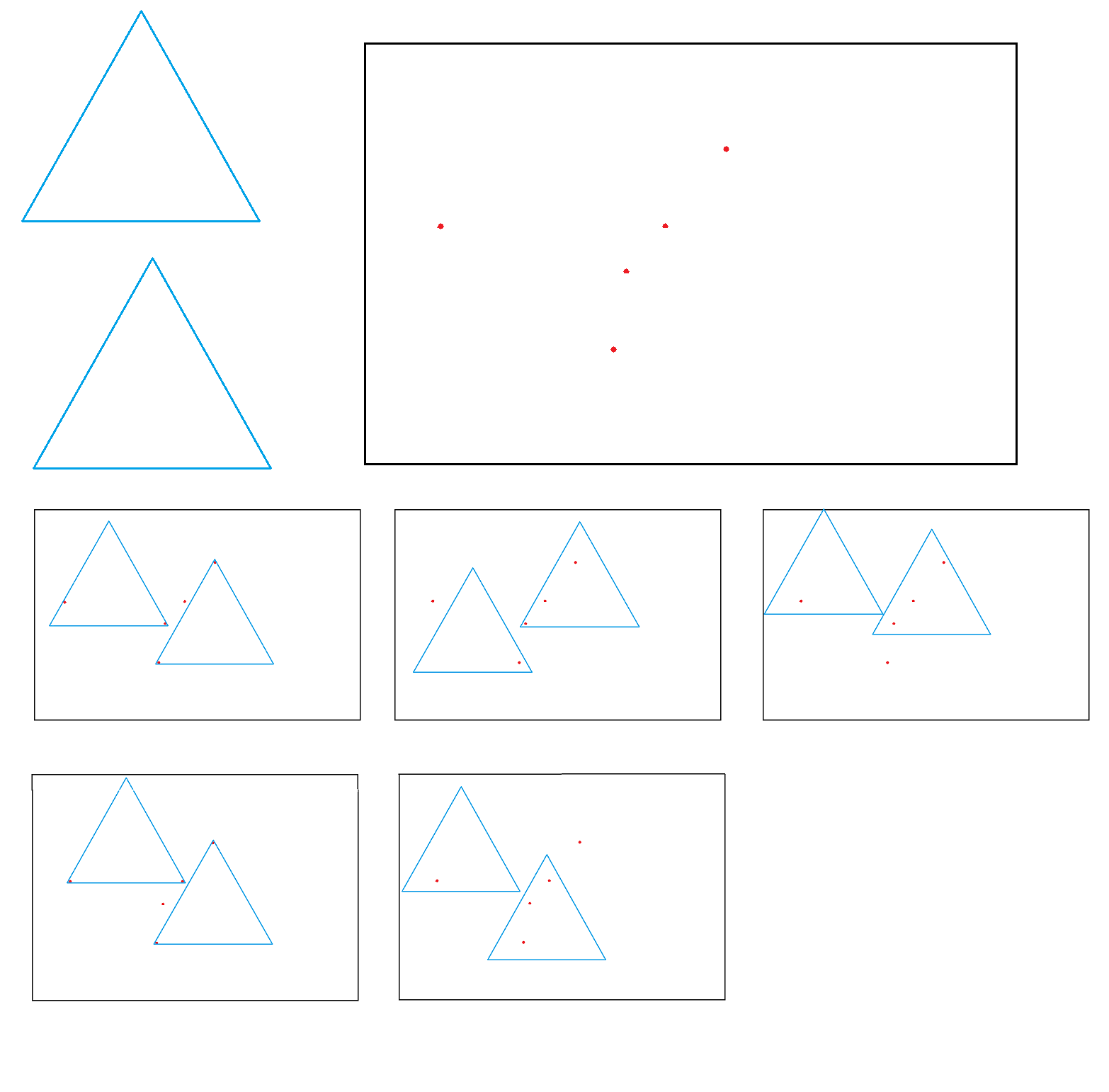
Par exemple :
#17 - 31-05-2014 10:33:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtteau 78
D'accord Gwen , on peut trouver un groupe de cinq taches qu'on ne peut pas recouvrir alors que chaque groupe de quatre peut être caché .
Un groupe de 6 ?
Vasimolo
@Nodgim : le cas de deux triangles peut-il se résumer à un triangle+un triangle ?
#18 - 31-05-2014 11:41:05
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâtau 78
Non, ce que je dit c'est que si on peut recouvrir n'importe quel groupe de 5 taches (pas quatre) alors on pourra recouvrir toutes les taches. Ma démonstration n'est pas clair ? 
Si il y a des points de la démonstration incompréhensibles, il ne faut pas hésiter à me le dire !
EDIT : Voici quelques illustrations pour éclaircir mes explications :
Si un gâteau ne contient qu'une seule tache, alors la zone dont je parle aura la forme suivante :
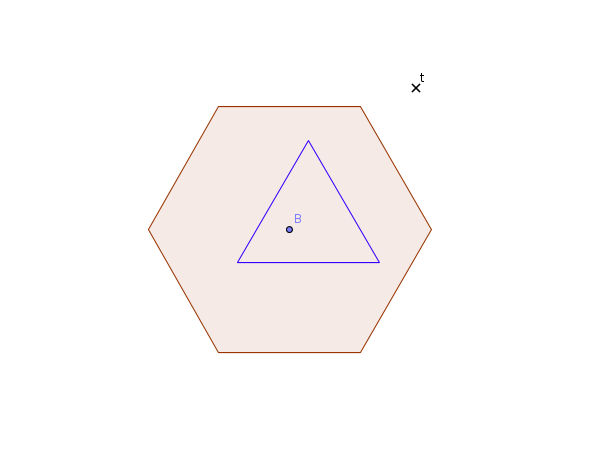
Quelque soit l'endroit où se trouve le gâteau dans cette zone, il recouvrira toujours la tache B. Et c'est la zone maximale qui vérifie cette propriété. Donc si on ajoute une tache t hors de la zone, je serais obliger de découvrir la tache B si je veux recouvrir la tache t.
Si le gâteau recouvre plusieurs taches, pour aller recouvrir une tache t hors de la zone, il serait obliger de découvrir au moins une tache.
Lorsque le gâteau recouvre plusieurs taches, la forme de cette zone est plus compliqué, dans le dessin suivant je les ai modélisé par des cercles.
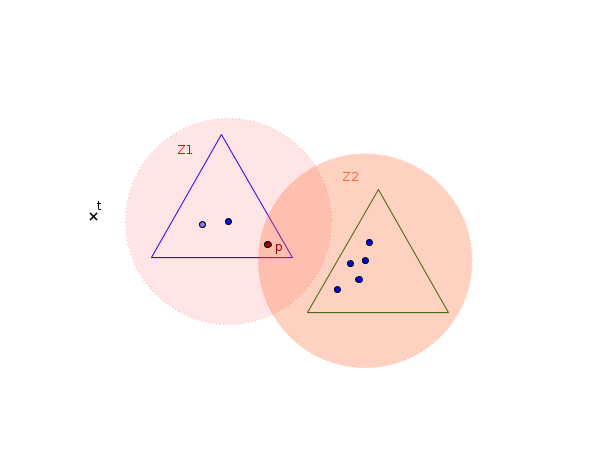
Ici si le gâteau bleu veut recouvrir la tache t, il sera obliger de découvrir la tache p (car t est hors de la zone Z1). Mais comme la tache p est dans la zone Z2, elle va pouvoir être recouverte par le gâteau vert sans que celui-ci ne découvre d'autres taches. Si la tache p n'était pas dans la zone Z2 alors le gâteau vert aurait été obligé de découvrir quelques taches pour aller recouvrir la tache p.
Lorsque l'on a déplacé le gâteau bleu pour qu'il recouvre la tache t, le gâteau bleu recouvre un nouvel ensemble de taches. Pour ce nouvel ensemble, on peut définir de la même manière une zone que j'ai appelé NZ1. Par le même raisonnement que dans le paragraphe ci dessus, si les taches découvertes par le gâteau vert lorsqu'il a été recouvrir la tache p (on est dans le cas ou p est hors de Z2) est inclus dans NZ1 alors le gâteau bleu pourra aller les recouvrir. Sinon on aura une tache q hors de NZ1.
Ici les taches p et q sont les p1 et q2 de la démonstration.
En faisant le même raisonnement mais cette fois en déplaçant le gâteau vert pour aller recouvrir la tache t, je crée également les taches p2 et q1 de mon poste précédent. Et ces 5 taches t, p1, p2, q1, q2 sont trop éloignées pour être recouvertes par les deux gâteaux, il est donc impossible d'être dans le cas où ces 5 taches existe.
Voilà, j'espère que ces explications éclairent plus qu'elle n'embrouillent 
Il y a sûrement plus simple.
#19 - 31-05-2014 19:15:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteai 78
Désolé Cogito mais je ne comprends pas ta construction 
Tu dis que c'est vrai à partir de 5 ce qui veut dire ( je suppose ) que pour toute configuration de 6 taches : si 5 taches quelconques peuvent être recouvertes par 2 triangles alors les 6 taches peuvent être recouvertes par 2 triangles .
Si tu pouvais essayer de détailler ta stratégie uniquement pour ce cas .
Par exemple , la récupération du point supplémentaire n'est vraiment pas claire , on pourrait imaginer qu'on abandonne tous les points de la première zone pour gagner ce point et alors je ne vois pas ce qu'on peut en tirer .
Ceci dit je suis de plus convaincu avec toi Gwen et Nodgim qu'on peut mettre 6 en lieu et place de 9 dans le problème initial .
Et il y a sûrement une démonstration qui tient en deux lignes 
Vasimolo
PS : Ce gâteau est en fait un préambule à un 78 bis "un peu" plus compliqué .
#20 - 31-05-2014 21:52:13
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
gâteai 78
Argghh, désolé, mais il y a une grosse faille dans mon raisonnement :
Si on est obligé de découvrir un point ce n'est pas forcément parce qu'il est trop loin, ça peut être aussi parce que sinon on empiète sur le deuxième gâteau, donc du coup tout tombe à l'eau 
Désolé 
Il y a sûrement plus simple.
#21 - 01-06-2014 18:40:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gtâeau 78
On peut résumer ou élargir la question de la façon suivante :
Un ensemble de six parties convexes du plan est-elle 2-connexe si toute partie de cinq éléments de cet ensemble est 2-connexe ?
Définition maison : Un ensemble de parties est 2-connexe si on peut en faire une partition en deux sous-ensembles A et B tels que l'intersection des éléments de A et l'intersection des éléments de B soient non vides .
Vasimolo
PS : l'hypothèse convexe peut-elle être remplacée par connexe ???
PPS : je lève le cache car je n'ai pas de réponse et que vos idées valent bien les miennes 
PPS : je pensais défoncer des portes ouvertes avec ce problème alors qu'il n'y a rien de simple à priori .
PPPS : Une suite était prévue mais j'attends l'issue de cette première étape 
#22 - 01-06-2014 18:59:44
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâtaeu 78
Euh, je ne suis pas sur d'avoir compris la 2-connexité, c'est un ensemble constitué de deux composantes connexes ?
Les sous ensembles A et B de la définition doivent-être connexes ?
Si c'est le cas, comme l'intersection de A et de B est non vide alors l'ensemble de départ est déjà connexe ?
Il y a sûrement plus simple.
#23 - 01-06-2014 19:23:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteu 78
A et B sont des parties d'un ensemble de six parties du plan . La 2-connexité ( Terme un peu barbare , on doit pouvoir faire mieux ) on peut séparer l'ensemble en deux morceaux A et B tels que l'intersection des éléments de A soit non vide , et l'intersection des éléments de B soit non vide . Par exemple cinq disques identiques alignés avec un point de contact n'est pas 2-connexe bien que connexe .
Vasimolo
#24 - 01-06-2014 20:02:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
gâteai 78
Pour ma part, je n'ai pas non plus trouvé de groupe de 6 pts non recouvrables intégralement. J'ai bien l'impression que 5 est le max, mais je ne peux le prouver.
#25 - 01-06-2014 21:00:22
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gââteau 78
D'accord, alors soit [latex]S_1, S_2, S_3, S_4, S_5, S_6[/latex] les six ensembles.
cas 1 : il existe i et j tels que [latex]S_i\cap S_j[/latex] est vide.
Quitte a renommé les ensembles, je peux supposer que i=1 et j=2.
Construisons nos deux ensemble A et B :
On met [latex]S_1[/latex] dans A et [latex]S_2[/latex] dans B.
Dans la suite [latex]I_A[/latex] désigne l'intersection des éléments de A
et [latex]I_B[/latex] désigne l'intersection des éléments de B.
Pour i allant de 3 à 6 faire :
Si [latex]S_i\cap I_A[/latex] est vide
alors [latex]B := B + S_i[/latex] // commentaire 1 (après)
Sinon Si [latex]S_i\cap I_B[/latex] est vide
alors [latex]A := A + S_i[/latex] // voir commentaire 1
Sinon [latex]A := A + S_i[/latex] // ou [latex]B := B + S_i[/latex] au choix.
Fin de la boucle Pour.
commentaire 1 : il est impossible que [latex]S_i\cap I_A[/latex] et [latex]S_i\cap I_B[/latex] soient vide en même temps.
Expliquons en faisant la première itération :
[TeX]i =3 , A = S_1, B = S_2, I_A = S_1, I_B = S_2[/TeX]
Explication du commentaire :
[latex]S_3\cap S_1[/latex] et [latex]S_3\cap S_2[/latex] ne peuvent pas être vide en même temps car sinon [latex]\{S_1,S_2,S_3,S_4,S_5\} [/latex]ne serait pas 2-connexe, ce qui contredit l'hypothèse.
Si [latex]S_3\cap S_1[/latex] est vide alors [latex]S_3\cap S_2[/latex] n'est pas vide et donc j'ajoute [latex]S_3[/latex] dans [latex]B[/latex].
Sinon Si [latex]S_3\cap S_2[/latex] est vide alors [latex]S_3\cap S_1[/latex] n'est pas vide et donc j'ajoute [latex]S_3[/latex] dans [latex]A[/latex].
Sinon je peux ajouter [latex]S_3[/latex] dans [latex]A[/latex] ou dans [latex]B[/latex] comme je veux.
Et après on réitère avec le nouveau [latex]A[/latex] et le nouveau [latex]B[/latex] pour savoir où il faut mettre [latex]S_4[/latex], ...
à la fin on a deux ensemble A et B qui vérifient la bonne propriété et donc notre groupe de 6 ensembles est 2-connexe.
Mais ça c'est seulement il existe i et j tels que [latex]S_i\cap S_j[/latex] est vide.
En fait dans le cas où il n'existe pas de tels i et j, si il existe un groupe d'ensembles d'intersection vide, alors on peut toujours les séparer en deux groupes d'intersections non vide. Par exemple si [latex]S_1, S_2, S_3[/latex] est d'intersection vide alors les deux groupes [latex]S_1[/latex] et [latex]S_2,S_3[/latex] sont chacun d'intersection non vide.
Dans ce cas là on peut reprendre l'algorithme ci-dessus, mais avec comme données initiales pour [latex]A[/latex] et [latex]B[/latex] les ensembles de chacun des groupes.
Dans notre exemple on démarrera l'algorithme avec [latex]A = S_1[/latex] et [latex]B = S_2,S_3[/latex]. (et on changera l'ensemble dans lequel on prend les valeurs de i (la variable de boucle) en conséquence, bien sûr.
Sinon si l'intersection des six ensembles est non vide alors on peut prendre n'importe quoi pour A et B (du moment qu'ils sont non vides).
quelque chose me dit que ce n'est pas très clair 
P.S: l'hypothèse de connexité nous dis que l'intersections des ensembles dans A (et dans B) est connexe.
Il y a sûrement plus simple.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










