|
#1 - 19-02-2016 10:27:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 19-02-2016 10:37:55
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtau 121
EDIT
Unité : le gâteau initial fait 4x4.
Avec la même orientation, le gâteau - d'aire 16 - serait 5x5 avec un trou 3x3 centré. On ne peut pas loger les grands triangles.
Avec une orientation à 45°, on fait un carré 3√2x 3√2 avec un trou de √2x√2 au centre. L'aire couverte est alors 18-2 = 16 comme au départ.
Il ne reste plus qu'à voir si on peut placer les pièces et comment.
Re EDIT
On ne peut pas, les deux grands triangles ont leurs angles droits diagonalement opposés, il n'y a pas place pour le carré.
#3 - 19-02-2016 10:41:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâteay 121
@Halloduda : il faut que tu précises tes unités et à priori le petit carré peut prendre une taille aussi petite qu'on le souhaite .
Vasimolo
#4 - 19-02-2016 10:52:40
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâteai 121
Je comprend pas le sujet : quel découpage est imposé ?
#5 - 19-02-2016 10:59:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
hâteau 121
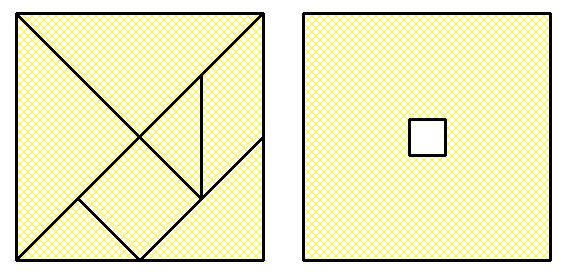
@Portugal : Tu ne connais pas le tangram ? On prend les pièces du jeu ( figure de gauche ) et on essaie de former le carré troué ( à droite ) . Le principe du jeu est qu'on donne uniquement la silhouette de l'objet à trouver sans sa taille ni le détail des pièces qui sont à découvrir .
Vasimolo
#6 - 19-02-2016 11:24:54
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâeau 121
Ca voudrait dire pour que la surface corresponde que l'on voudrait créer un carré troué un peu plus grand que le carré de base ?
Sur ton dessin ils sont de meme taille ce qui est étrange d'un point de vue surface, non ?
#7 - 19-02-2016 11:25:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea 121
Oui bien sûr 
Vasimolo
#8 - 19-02-2016 11:33:24
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gtâeau 121
ok compris merci... ;=)
une justification pour le cas ou ca ne serait pas possible :
Il y a 7 pieces et le carré du milieu à 4 sommets dont aucune pièce ne peut "ajuster un sommets". Il faut de plus aller chercher les 4 angles du grand carré donc ca va commencer à être difficile.
#9 - 19-02-2016 11:53:02
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#10 - 19-02-2016 12:00:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#11 - 19-02-2016 17:26:26
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
âteau 121
Les différents côtés des pièces du Tangram ont des longueurs appartenant à l'ensemble { 1 ; 1/2 ; racine(2)/2 ; racine(2)/4 }.
Recherchons les dimensions possibles pour le côté d'un carré percé vérifiant le problème. Le côté est strictement supérieur à 1, et il est somme d'éléments de l'ensemble ci-dessus, puisqu'il faut accoler des pièces du Tangram le long de ce côté.
La première valeur possible est 3*racine(2)/4 soit environ 1,0607 (tiens, ça me rappelle le cube du Prince Rupert). En ce cas, le côté du trou doit faire racine(2)/4, pour que l'aire du carré troué fasse 1. Quelques essais montrent cependant que les pièces ne peuvent s'ajuster pour former ce carré troué : on commence par placer les grands triangles qui sont forcément dans deux coins opposés du carré, puis on voit rapidement qu'on ne peut placer les pièces restantes (si on s'autorisait à couper en deux le carré, ou le parallélogramme, ou le losange, ce serait possible cependant, c'est frustrant).
La deuxième valeur possible est (1+racine(2))/2 soit environ 1,207. Dans ce cas, le côté du trou mesure environ 0,676. Et alors, les deux grands triangles sont trop grands pour rentrer dans le carré troué, ils débordent...
Comme le même phénomène se produit pour les valeurs plus grandes, il est impossible de fabriquer un carré troué avec le Tangram.
#12 - 19-02-2016 18:43:11
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,043E+3
gâtrau 121
Les longueurs sont traduisible par x+y rac(2) en alignant les pièces, que ce soit pour le tour ou le carré central.
On a donc (a+b rac(2))^2 = 16 avec pour unité un petit triangle.
Seule solution : a=4, b=0
Autrement dit, c'est impossible, sauf si le carré central a une aire nulle.
Un lien très complet sur le sujet, même si je n'ai pas lu les 250 pages...
http://mathadomicile.fr/Puzzles/evoluti … olutif.pdf
C'est possible avec l'ancètre du tangram (page 159)
#13 - 19-02-2016 23:06:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 12
@Ebichu : c'est convainquant , existe-t-il un argument plus expéditif pour le premier cas ?
@Gwen : magnifique référence que je ne connaissais pas 
Vasimolo
PS : un petit supplément pour ceux qui ont fini , comment transformer légèrement le découpage du tangram pour rendre la réalisation plus aisée 
#14 - 20-02-2016 08:59:23
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtau 121
Les longueurs des côtés des pièces mesurent (environ, et à un coefficient près) :
Petits triangles et parallélogramme : 1 et 1,4
carré : 1
Grands triangles : 2 et 2,8
Triangle moyen : 1,4 et 2
Le carré d'origine a pour côté 2,8. Pour faire le carré troué, il faut augmenter légèrement la longueur "extérieure" du carré.
Le minimum atteignable avec les pièces est 3, mais pour l'obtenir il nous faut 4 côtés de longueur 3, or on a seulement 4 fois 1 et 3 fois 2, ce n'est pas suffisant.
Ensuite on peut chercher à faire 3,4 : 1,4+2 ; mais cette fois-ci, l'assemblage ne permet pas d'obtenir 4 bords sans point "d'épaisseur nulle" (endroits où 2 bords à angle saillant en contact).
Idem pour la suite. C'est donc impossible.
#15 - 20-02-2016 19:05:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#16 - 20-02-2016 21:25:07
- BlaiseP
- Habitué de Prise2Tete
- Enigmes résolues : 1
- Messages : 31
hâteau 121
Tu n'es pas prêt de manger ton gâteau …
Inventaire des pièces du tangramme avec le carré comme unité :
2 grands triangles surface 2 de côté 2, hypoténuse 2sqr(2), notés Ts2
1 moyen triangle surface 1 de coté sqr(2), hypoténuse 2, noté Ts1
2 petit triangles surface 1/2 de côté 1, hypoténuse sqr(2) notés Ts1/2
1 carré surface 1 de côté 1 noté Cs1
1 parallélogramme surface 1 de coté 1 et hauteur 1 noté Ps1
surface disponible 8
Notons que la plus petite longueur disponible est 1. Le côté du gâteau est soit entier, soit un multiple entier de sqr(2), de sorte que la surface gâteau + trou est nécessairement entière : soit un carré, soit le double d'un carré.
Supposons que le trou soit de surface 1.
la surface totale est 9, le côté est 3
on doit placer les Ts2 dans les angles opposés du carré, hypoténuse à 45°
on doit placer Cs1 dans un angle restant, avec les Ts1/2 adjacents
on doit placer Ts1 symétriquement, avec les côtés à 45°
mais alors on ne peut plus placer Ps1 !
 Ah mais si, je vais couper Ps1 en deux Ts1/2 … Ah mais si, je vais couper Ps1 en deux Ts1/2 …
Si la surface du trou était 2, la surface totale vaudrait 10, ça ne marche pas, aucune dimension n'est multiple de sqr(5)
Si la surface du trou était 4, ça marche pas non plus, aucune dimension n'est multiple de sqr(3)
Si la surface du trou est 8; le carré a un côté de 4, le trou a un côté de 2sqr(2);
il n'est pas possible d'obtenir 4 à partir de 2sqr(2) en ajoutant des entiers ou des multiples de sqr(2).
Si le trou est encore plus grand, la largeur de la bordure diminue et on ne peut plus placer les Ts2. Je pense qu'on peut montrer qu'il n'y a plus d'autre possibilité avec des trous encore plus grands.
T'as qu'à manger un baba au rhum, avec une belle forme de tore et un trou rond au milieu...
#17 - 21-02-2016 00:16:16
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gtâeau 121
Bravo ! Ma conclusion est complètement c**.
Je m'y remets...
#18 - 21-02-2016 10:26:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 121
@BlaiseP : Et pourquoi l'aire du trou serait-elle entière ?
Vasimolo
#19 - 22-02-2016 10:58:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtrau 121
Encore un gâteau impossible 
J’avais préparé ma solution , elle ressemble beaucoup à celle d’Ebichu que je félicite au passage , mais comme elle est faite , autant la partager .
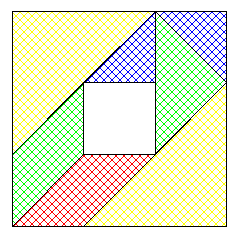
On suppose que le côté du petit carré du tangram mesure 1 , alors toutes les longueurs s’écrivent a+b√2 avec a et b entiers naturels . Le côté c du grand carré doit être supérieur à 2√2 et la largeur de la bande autour du trou au moins égale à 1 . On obtient alors la double inégalité : 2√2<c≤3 dont l'unique solution est c=3 . On est donc ramené à l'exemple que je citais plus haut . Les deux grands triangles vont forcément se positionner sur deux sommets opposés du trou central :
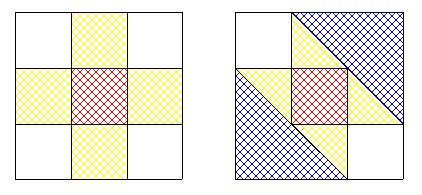
On peut constater que parmi les pièces restantes seuls les deux petits triangles et le carré sont déséquilibrés en cases jaunes et blanches donc les deux petits triangles ont la même couleur . Malheureusement quand on pose le triangle de taille médiane dans l'une des deux zones laissées libres on fait apparaître deux petits triangles de couleurs différentes .
Merci aux participants .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum