|
#1 - 12-10-2017 18:05:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 12-10-2017 19:50:05
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
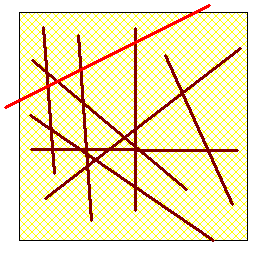
gâtzau 146
Je ne suis pas sûr de bien comprendre le problème.
Est ce que n'importe quelle découpe doit traverser 4 lignes, ou il existe au moins une découpe qui traverse 4 lignes ?
#3 - 12-10-2017 21:41:35
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 1446
Salut Vasimolo,
pour simplifier, je considère que le gâteau est de côté 1, et que la longueur totale du caramel vaut 7.
Lorsque l'on projette une ligne de caramel de longueur L sur l'horizontale, la longueur occupée est L|cos(α)| où α est l'angle de la ligne avec l'horizontale. Si on la projette sur la verticale, la longueur occupée est L|sin(α)|.
Or la fonction qui à x associe |cos(x)|+|sin(x)| a pour minimum 1. La longueur totale de la somme des projections de toutes les lignes sur l'horizontale et de leurs projections sur la verticale est donc supérieure ou égale à 7. Il y a donc une des deux directions pour laquelle la somme des projections est supérieure ou égale à 3,5, donc strictement supérieure à 3. On peut donc trancher le gâteau perpendiculairement à cette direction en coupant au moins 4 lignes.
Inversement, la fonction qui à x associe |cos(x)|+|sin(x)| a pour maximum racine(2). La longueur totale de la somme des projections de toutes les lignes sur l'horizontale et de leurs projections sur la verticale est donc inférieure ou égale à 7*racine(2). Il y a donc une des deux directions pour laquelle la somme des projections est supérieure ou égale à 7*racine(2)/2, donc strictement inférieure à 5. On peut donc trancher le gâteau perpendiculairement à cette direction en coupant au plus 4 lignes.
#4 - 12-10-2017 22:16:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
hâteau 146
@Nodgim : il faut simplement trouver deux découpes , une coupant au moins quatre lignes et l'autre au plus quatre lignes .
@Ebichu : c'est bon , j'avais fait presque pareil mais sans passer par la fonction que tu considères .
Vasimolo
#5 - 13-10-2017 12:00:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 164
105 pour carré 15 équivaut à 7 pour carré 1.
On met bout à bout tous les segments dans un repère orthonormé à partir de (0,0) et en prenant les segments dans l'ordre d'inclinaison trigonométrique de 0 inclus à Pi exclu. Pour les segments au dela de PI/2, on les retourne pour que le projeté sur x ne se superpose pas. Pour avoir un projeté minimal de cette courbe brisée, soit sur l'axe des x, soit sur celui des y, il faut aboutir, au bout de la ligne brisée, à une coordonnée à x=y. Pour arriver à un x=y minimal, avec comme longueur de ligne brisée 7, pas d'autre solution que de suivre les axes : 3,5 horizontal puis 3,5 vertical. Limité dans un carré de coté 1, on ne peut donc pas repasser moins de 3,5 l'axe le plus chargé, soit 4 si on cherche un max. C'est par exemple obtenu avec 2 carrés emboités, l'un de coté 1, l'autre de coté 3/4.
#6 - 13-10-2017 16:32:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteay 146
@Nodgim : je vois bien comment tu construis ta ligne brisée , je suis d'accord avec le minimum mais pas le maximum . Surtout je ne vois pas comment tu utilises cette ligne pour conclure 
Vasimolo
#7 - 13-10-2017 18:28:58
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 1146
105 et 15 peuvent être ramenées aux valeurs 7 et 1.
On inscrit chaque segment dans un rectangle Horizontal/Vertical dont 2 sommets en diagonale sont confondus avec ceux du segment. On place ces rectangles dans le repère orthonormé: le 1er, son coin bas gauche en (0,0), les autres tels que leur coin bas gauche est confondu avec le coint haut droit du précédent. Le coin haut droit du dernier est à une abscisse (x,y).
x détermine donc la longueur totale des projetés sur l'axe des x, et y sur sur l'axes des y.
Le min de x ou y est 0, le max est 7. Quand tous les segments ont la même orientation, et quand x=y, alors (x,y) = 7/V2 = 4,9.. (orientation 45°).
Toujours quand x=y, son min est 3,5, quand les segments sont tous horizontaux ou verticaux.
Comme le carré fait 1, lorsque les segments sont regardés maintenant à leur vraie position, les superpositions minimales et maximales, dans le cas le plus défavorable, des projetés sur x et y sont les entiers qui encadrent x/1 et y/1 (principe des tiroirs), soit pour 3,5 : 3 et 4, et pour 4,9 : 4 et 5.
Si l'on cherche maintenant à regarder quel est le minimum de segments qu'une coupe va traverser, coupe horizontale ou verticale :
- Min pour le dessin le plus défavorable: 4 avec les segments orientés à 45°.
- Max pour le dessin le plus défavorable: 4 avec les segments horizontaux ou verticaux.
On remarque qu'on n'a pas besoin de vérifier des coupes autres que horizontales ou verticales.
On remarque aussi que ces max et min sont indépendants de la possibilité ou non de réaliser une configuration réelle qui correspond aux cas extrêmes.
#8 - 13-10-2017 23:14:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
GGâteau 146
C'est plus clair Nodgim , mais pourquoi déplacer les segments pour faire une chaîne ?
Vasimolo
#9 - 14-10-2017 07:57:45
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
gâtrau 146
Je ne sais pas trop. Cette image m'a permis de mieux visualiser les min max des (x,y), je pataugeais sans elle sur cette mesure.
#10 - 14-10-2017 13:17:50
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gâteau 416
Bonjour,
Considérons le cas plus simple où la tranche est parallèle au bord.
Plaçons coin du gâteau bas gauche dans l'origine d'un repère orthogonal.
Soit un trait de caramel de longueur L. Sa projection sur l'axe des abscisse ou des ordonnées est inférieure à L, mais la somme de ses projections sur ces deux axes est supérieure à L (et inférieure à LV2 ). La somme totale des projection du caramel est donc supérieure à 105cm. L'un des axes à donc un total de projection supérieur à 105/2 = 52.5, qui est supérieur à 3 fois la longueur du côté.
Si pour toute tranche parallèle à un côté, elle passait par trois traits ou moins, la projection sur ce côté serait inférieure à 15*3 = 45. On en déduit donc qu'il existe une tranche passant par 4 traits, et ce à partir de 90cm de traits.
Je conjecture qu'en prenant en compte les tranches en biais, on peut descendre à 60 + 15V2.
Pour l'autre problème, Considérons le cas où toutes les tranches sont parallèles aux diagonales du gâteau. La somme des projections sur les diagonales est la même qu'avant. Il suffit de remarquer que la somme totale des projections est inférieure à 105V2 = 148. Il existe donc un côté où la somme des projection est inférieur à 75cm. Si toutes les tranches passaient par 5 traits ou plus, la somme des projections sur un côté serait supérieure à 5*15*V2 = 106cm.
On en déduit donc que l'on peut toujours trouver une tranche passant par 4 lignes ou moins tant que la longueur totale des traits est inférieure à 106*2/V2 = 150cm.
Je conjecture que l'on peut monter jusqu'à 180cm.
#11 - 15-10-2017 10:39:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteai 146
C'est bon Caduk 
Pour les conjectures , ce n'est pas évident à estimer ( il faut mettre le doigt sur la pire des configurations ) et encore plus difficile à démontrer ( en quoi est-ce la pire ? ) .
Vasimolo
#12 - 15-10-2017 18:28:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtau 146
Il suffisait de projeter les traits de caramel sur deux côtés consécutifs du gâteau et d'utiliser l'encadrement : [latex]l\leq x+y \leq l.\sqrt{2}[/latex] .
Bravo à ceux qui ont trouvé 
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum