Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 03-10-2015 00:20:00
âteau 107Bonjour à tous
#0 Pub#2 - 03-10-2015 02:11:28
Gâteau 07
#3 - 03-10-2015 02:40:08
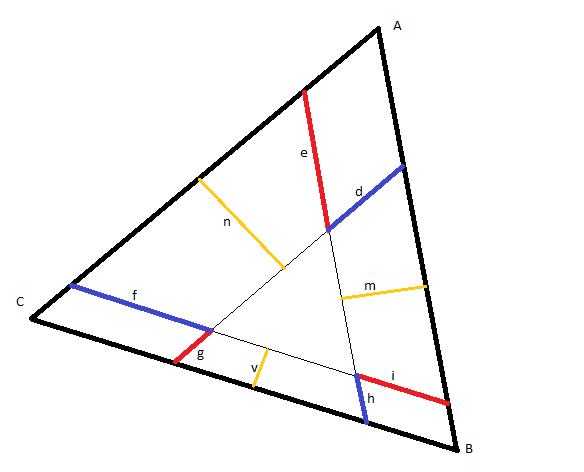
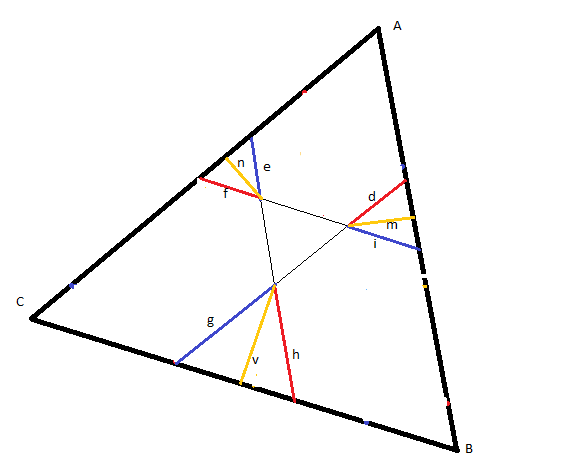
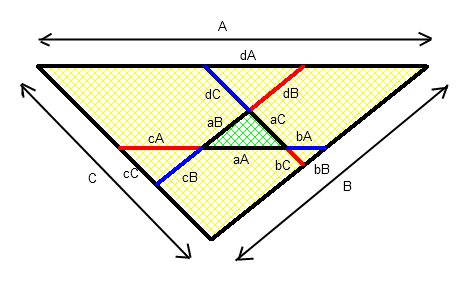
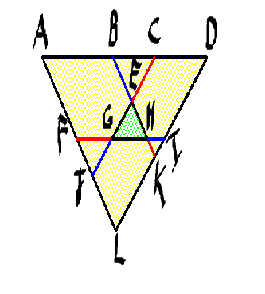
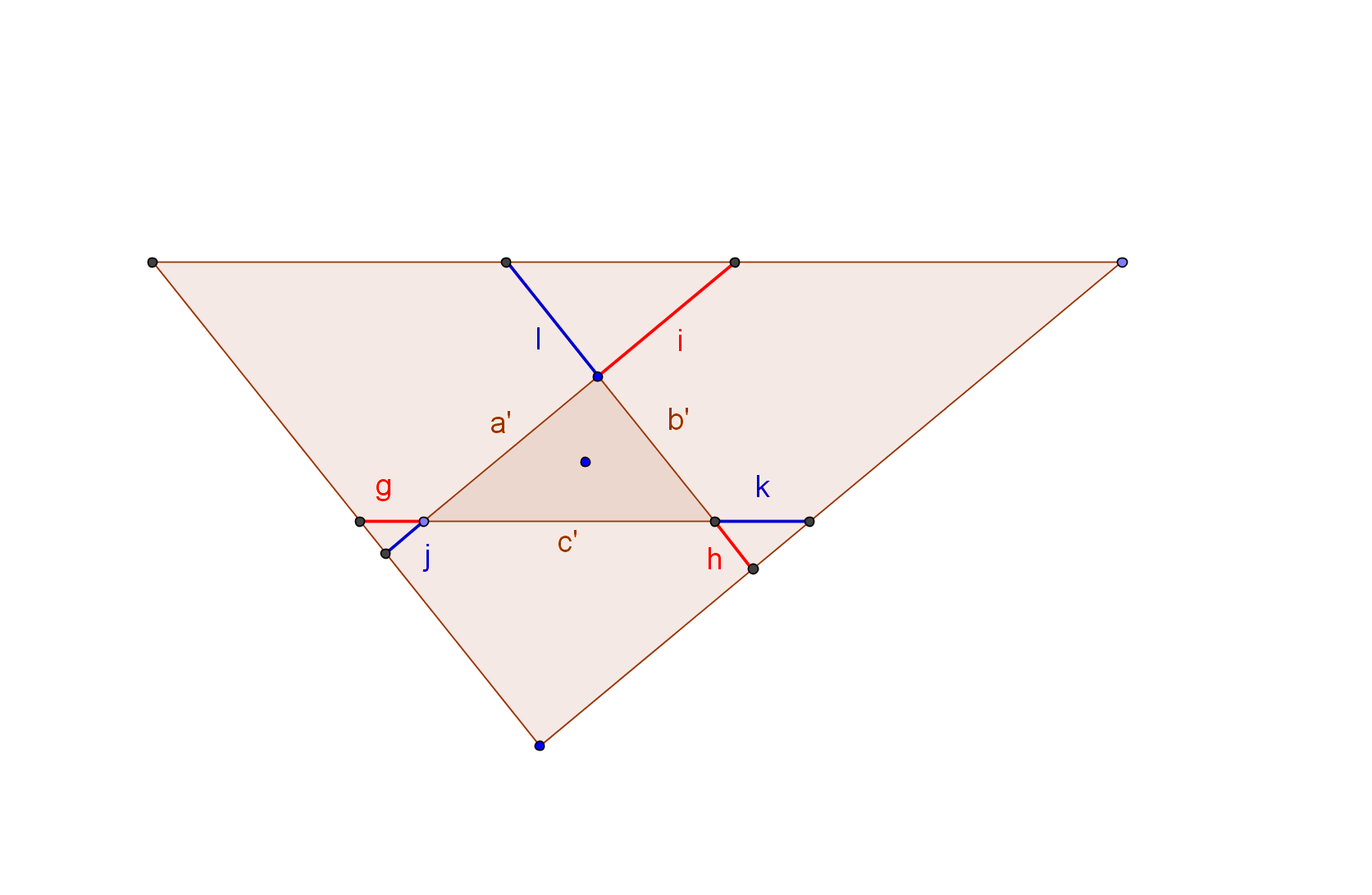
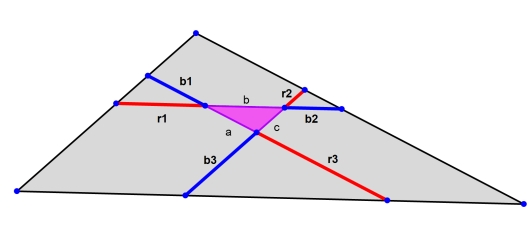
gâteai 107On remarque que les 3 "petits" triangles formés de la portion centrale des bords respectifs prolongés des bâtonnets de couleurs adjacents sont homothétiques. #4 - 03-10-2015 07:36:18
Gâtteau 107J'avoue ne pas trop comprendre l'artifice par lequel sont "construits" les gateaux bleu et rouge #5 - 03-10-2015 08:58:13
âGteau 107C'est bon pour tous #6 - 03-10-2015 12:17:47#7 - 03-10-2015 21:04:35
âGteau 107
#8 - 04-10-2015 18:52:11#9 - 05-10-2015 01:35:09
gâteay 107On a #10 - 05-10-2015 15:00:00#11 - 05-10-2015 15:32:45
Gââteau 107
#12 - 05-10-2015 19:50:15#13 - 06-10-2015 17:04:11
Gâtea 107Je vous laisse admirer les réponses #14 - 14-10-2015 22:40:34
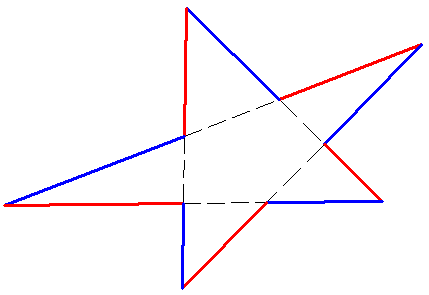
âGteau 107A peine plus difficile ? Si quand même. Il n'y a plus de triangles semblables et je ne trouve aucune démonstration simple. Une piste ? Merci. #15 - 15-10-2015 17:09:03#16 - 15-10-2015 18:02:54
Gtâeau 107
#17 - 15-10-2015 19:37:12
Gâteau 1077Ah oui celle-là elle est excellente ! Ultra courte et lumineuse. Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.





.png)
.png)
.png)