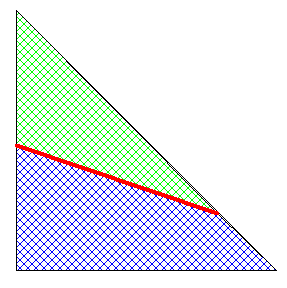
|
#1 - 22-06-2017 00:05:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 22-06-2017 08:48:45
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
gâteay 136
Bonjour,
J'obtiens une longueur de coupe minimale lorsque ses 2 extrémités sont à égale distance du sommet d'un angle de 45°.
Si le côté du carré initial vaut 1, cette distance est 1/racine_4ème(2), et la longueur de coupe vaut sqrt(2)-1
Correction (suite à la remarque de Vasimolo en #8) :
En fait, j'ai minimisé le carré de la longueur de la découpe. et cette dernière vaut donc sqrt(sqrt(2)-1)
#3 - 22-06-2017 09:59:03
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
hâteau 136
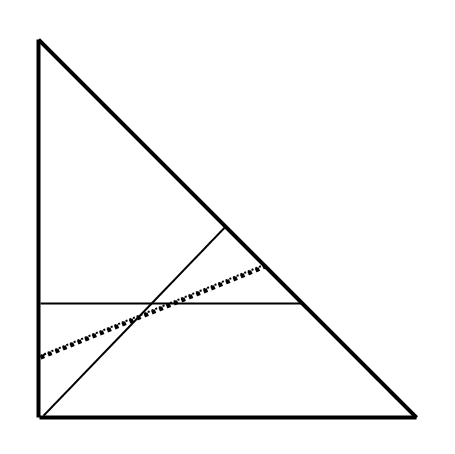
On voit bien qu'une solution optimale existe entre les deux solutions en traits pleins.
Après de longs calculs (avec annulation de dérivée), je m'aperçois que cette solution est constituée du triangle isocèle délimité par la ligne en pointillés.
Les calculs sont alors beaucoup plus simples: LH/2 = 1/4 et tan(pi/8) = L/2H donnent:
L = V[tan(pi/8)] = V(V2 - 1) = 0,6436 env.
#4 - 22-06-2017 10:01:53
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 13
Après avoir éliminé le cas où les deux extrémités de la coupe sont sur les deux côtés de l'angle droit, qui donne même un moins bon résultat que la bissectrice, on suppose qu'une extrémité de la coupe est sur un côté de l'angle droit, et l'autre sur l'hypoténuse.
On peut par exemple poser x = distance entre l'extrémité de la coupe sur un côté de l'angle droit et le sommet du gâteau avec un angle aigu le plus proche.
On trouve alors que la longueur de la coupe au carré vaut x²-1+1/2x². On cherche donc à minimiser y-1+1/2y, avec la dérivée il vient [latex]y=\frac{1}{\sqrt{2}}[/latex] et donc [latex]x=\frac{1}{\sqrt{\sqrt{2}}}[/latex].
Finalement, la longueur de la coupe optimale est [latex]\sqrt{\sqrt{2}-1}[/latex]. On n'aurait pas cru qu'un énoncé aussi simple ait une solution aussi complexe 
#5 - 22-06-2017 10:08:33
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâtea 136
Je trouve une solution avec une coupe de longueur [latex]\sqrt{\sqrt{2}-1}[/latex]
= 0,64359...
#6 - 22-06-2017 11:34:04
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
âteau 136
La coupe est à 22.5° (perpendiculaire à la bissectrice d'un angle aigu)
et sa longueur 0.643594...
#7 - 22-06-2017 14:51:35
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
GGâteau 136
Bonjour,
Plaçons une extrémité A de la coupe sur le côté du bas, et considérons le repère orthonormé, dont l'origine est à l'angle droit et les vecteurs directeurs sont portés par les deux côtés adjacents.
Ce point à pour coordonnées (a,0), avec a à déterminer de manière à minimiser la coupe.
L'autre extrémité de la coupe à pour coordonnées B = (x, 1-x)
Soit C = (1,0) le sommet correspondant du triangle rectangle.
on veut que l'aire du triangle à droite soit 1/4, soit 1/2 det(AC,AB) = 1/4
Soit encore (1-a)(1-x) = 1/2 et donc 1-x = 1/2(1-a)
On veut minimiser sqrt( (x-a)^2 + (1-x)^2 )
On trouve alors a = 1-2^(1/4)
Ce qui donne une longueur de sqrt(2-sqrt(2))/2^(1/4) = 0.64359425290558
#8 - 22-06-2017 16:46:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 13
Que des bonnes réponses ( enigmatus a squeezé une racine dans la précipitation ) . On doit pouvoir trouver une solution purement géométrique en supposant connus les valeurs trigonométriques de [latex]\frac{\pi}{8}[/latex] , non ?
En tout cas joli tir groupé 
Vasimolo
#9 - 22-06-2017 21:17:07
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 1366
Vasimolo #8 a écrit:( enigmatus a squeezé une racine dans la précipitation )
Ah oui, c'est le carré de la longueur que je calculais. J'ai corrigé.
#10 - 22-06-2017 22:06:27
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâreau 136
Effectivement, en faisant un certain nombre de symétries, on se retrouve à minimiser le périmètre d'un octogone à aire constante, ce qui se produit pour un octogone régulier.
#11 - 23-06-2017 03:55:46
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
gâtzau 136
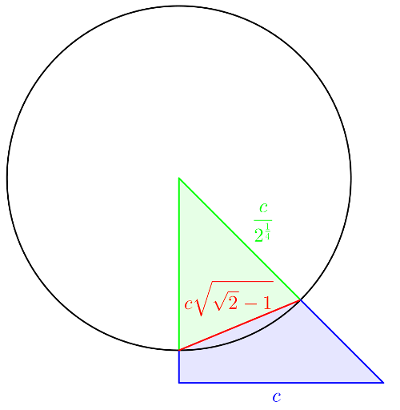
Salut, sauf erreur :
#12 - 23-06-2017 18:53:18
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâtteau 136
bonsoir.
Soit 1 la longueur des deux petits côtés du gateau.
[TeX]OA = AB = 1[/TeX]
et [latex]OB = \sqrt2[/latex]
j'effectue ensuite une homothétie de centre O et de rapport [latex]\frac{\sqrt2}{2}[/latex] du triangle OAB. Ce qui me donne le nouveau triangle rectangle isocèle OA'B'.
J'obtiens le trapèze isocèle A'DB'A , D étant le point d'intersection de la parallèle à
(AB') passant par A' et de la droite (OB'). Ainsi la grande médiane MN joignant les milieux des segments A'A et DB' doit être le segment recherché pour l'optimisation de la coupe recherchée .
[TeX]MN = \frac{2\sqrt2 \times\sqrt{\sqrt2 + 2}}{3\sqrt2 + 4} \approx 0.63405067..[/TeX]
n.b Latex fonctionne pour la prévisualisation , mais après ...
#13 - 23-06-2017 20:12:12
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gteau 136
Effectivement, on peut simplifier la démo, de manière géométrique.
Il suffit de remarquer que la coupe minimale est perpendiculaire à la bissectrice, même si ce n'est pas tout à fait évident à démontrer.
En notant a la demi-longueur de cette coupe minimale, et b la longueur de la moité de la coupe jusqu'à l'ange, on obtient la relation:
tan(pi/8) = a/b
ab = 1/4
Par suite, on a 4a^2 = tan(pi/8)
La longueur de la coupe est donc de 2a = sqrt(sqrt(2)-1) qui est bien égal à ce que j'avais déjà donné avant. (Il suffit de multiplier en haut et en bas par sqrt(sqrt(2)) )
#14 - 23-06-2017 21:20:25
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtezu 136
@Ebichu : Oui 
@Sydre : Oui et comment tu justifies que c'est la meilleure coupe ?
@Une Coudée : non mais tu n'es pas loin .
@Caduk : On peut justifier simplement que la coupe minimale est celle que tu annonces .
Vasimolo
#15 - 24-06-2017 00:25:45
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Gâtaeu 136
J'ai fait ça de façon bourrin :
- Je paramétrise la position de la coupure par 2 variables [latex]x[/latex] et [latex]y[/latex]
- J'écris l'égalité des aires [latex]V(x,y)=B(x,y)[/latex]
- Je détermine la longueur de la coupure [latex]L(x,y)[/latex]
- J'exprime la longueur de la coupure en fonction d'une seule variable grâce à la relation entre les aires
- Je cherche le minimum par dérivation
Il y a sans doute plus élégant 
#16 - 24-06-2017 10:14:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 13
Oui Sydre 
Je me souvenais avoir proposé une énigme assez voisine il y a quelque temps , en fait c'était mon premier gâteau : http://www.prise2tete.fr/forum/viewtopic.php?id=6252 .
De nombreux liens sont rompus mais on on doit pouvoir suivre l'idée .
Vasimolo
#17 - 25-06-2017 10:46:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
fâteau 136
Un problème que j'ai trouvé sur un site de maths , chacun y allait de ses coordonnées et de ses dérivés pour arriver à la solution . J'ai eu le même réflexe avant de me souvenir de ce vieux gâteau 1 .
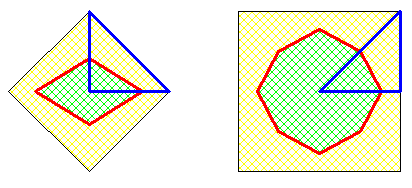
Pour une aire donnée le polygone régulier est celui qui a la plus petit périmètre .
Le reste est facile .
Merci aux participants .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum