|
#1 - 09-07-2017 12:08:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
#2 - 09-07-2017 14:30:16
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
#3 - 09-07-2017 16:41:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
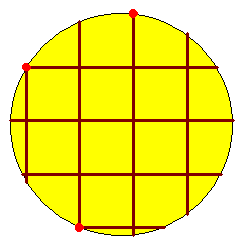
Gâteau 13
L'idée est venue de là 
Bravo !!!
Vasimolo
#4 - 10-07-2017 17:35:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
fâteau 138
Pour ceux qui cherchent et sèchent , un exemple avec 12 points :
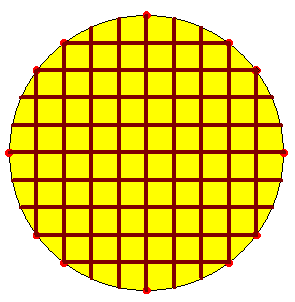
Vasimolo
#5 - 11-07-2017 00:12:30
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Gâteau 183
J'ai [latex]85=7^2+6^2=9^2+2^2[/latex] qui donne un cercle de diamètre [latex]36,88 \,\mathbb{cm}[/latex]
On dirait qu'il y a mieux car la case réponse ne valide pas 
#6 - 11-07-2017 09:22:38
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 183
Bonjour,
Je trouve un diamètre de 32,25 cm (qui valide la case réponse).
Le rayon du cercle (en unités de grille) est de sqrt(65), et les coordonnées des points du maillage situés sur le cercle sont
#7 - 11-07-2017 10:35:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâteau 13
@Sydre : c'est la bonne méthode mais tu as oublié un cas 
@Enigmatus : parfait .
Vasimolo
#8 - 11-07-2017 13:45:47
- Tr0llet
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 17
Gâetau 138
On part de l'hypothèse la plus plausible comme quoi le quadrillage est centré sur la galette (et donc qu'il y a 4 noeud par quart de galette). Avec ce bon vieux Pythagore, il suffit de trouver le plus petit entier décomposable en 2 sommes différentes (hors permutations bien sûr !) de 2 carrés d'entiers différents entre eux.
Un rapide tableur avec mise en forme conditionnelle des doublons indique la réponse : 65 (= 1*1 + 8*8 = 4*4 + 7*7).
Le rayon de la galette est donc de racine de 65 côtés d'un carreau (2 cm), donc son diamètre est de 4 racine de 65 cm, soit 32,25 cm en arrondissant au mm.
#9 - 11-07-2017 18:39:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gteau 138
C'est bon TrOllet , intuitivement cette hypothèse est la bonne ( je n'ai pas de démonstration  ) )
Vasimolo
#10 - 11-07-2017 20:01:31
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâtea u138
Je considère (sans pouvoir le prouver) que la figure est symétrique par rapport aux diagonales et aux axes. Un point ne peut pas se trouver sur une diagonale et donc pas non plus sur un axe.
On cherche a1, b1, a2 et b2, tels que: a1²+b1²= a2²+b2², sans être un carré parfait. Une recherche sur tableur me donne les points (7;4) et (8;1) et leurs symétriques par rapport aux diagonales et aux axes, soit 16 points en tout.
#11 - 11-07-2017 20:04:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
hâteau 138
C'est bon Franky et c'est vrai qu'il manque une preuve à tout ça 
Vasimolo
#12 - 13-07-2017 03:01:11
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
GGâteau 138
Effectivement j'ai oublié [latex]65=7^2+4^2=8^2+1[/latex] 
#13 - 13-07-2017 09:52:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâtea u138
Voilà qui est bien 
Vasimolo
#14 - 13-07-2017 16:08:37
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteau 18
Bonjour à tous,
Je suis parti du principe que le centre du meilleur cercle était sur un noeud (mais je ne l'ai pas prouvé).
Dès lors, j'ai recherché dans le premier quadrant du plan cartésien, toutes les sommes égales de 2 carrés d'entiers pairs.
260 a été le premier à s'y présenter 4 fois (2²+16² ; 16²+2² ; 8²+14² ; 14²+8²)
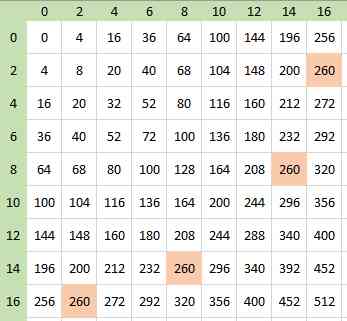
On en a donc 4x plus au total des 4 quadrants sur un cercle de diamètre 2 x rac(260).
Resterait à prouver qu'un cercle non centré sur un noeud ne peut donner mieux, mais ça c'est une autre histoire...
Merci pour ta galette 
#15 - 13-07-2017 18:20:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâteau 13
Oui Looozer 
La maille de 2 cm est un leurre , on peut se cantonner aux entiers pairs ou impairs . Il y a d'autres entiers avant la solution ayant deux décompositions mais ils ne conviennent pas ( pourquoi ? ) . Le centre de la galette est un nœud , c'est presque trop évident mais bien sûr il faudrait une démonstration 
Vasimolo
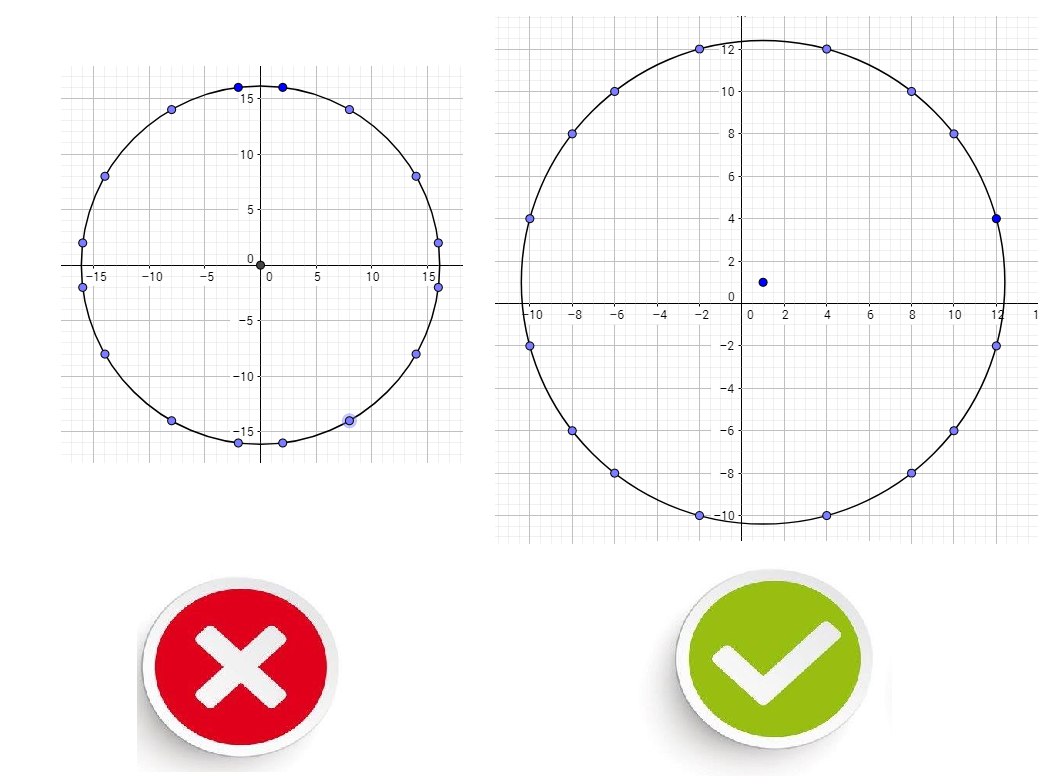
#16 - 13-07-2017 19:24:01
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,014E+3
Gteau 138
Ca n'est pas presque trop évident, c'est faux... 
Chouette réponse que ce 32,25 qui m'a bien fait douter, mais cette réponse n'est pas optimale. 22,80 marche mieux.
#17 - 13-07-2017 21:06:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
gâtrau 138
Bien vu Gwen !!!!
Du coup tout le monde a faux ( à commencer par moi  ) . ) .
Je remets un peu de temps et je change la case réponse .
Vasimolo
#18 - 13-07-2017 22:17:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,014E+3
gâtzau 138
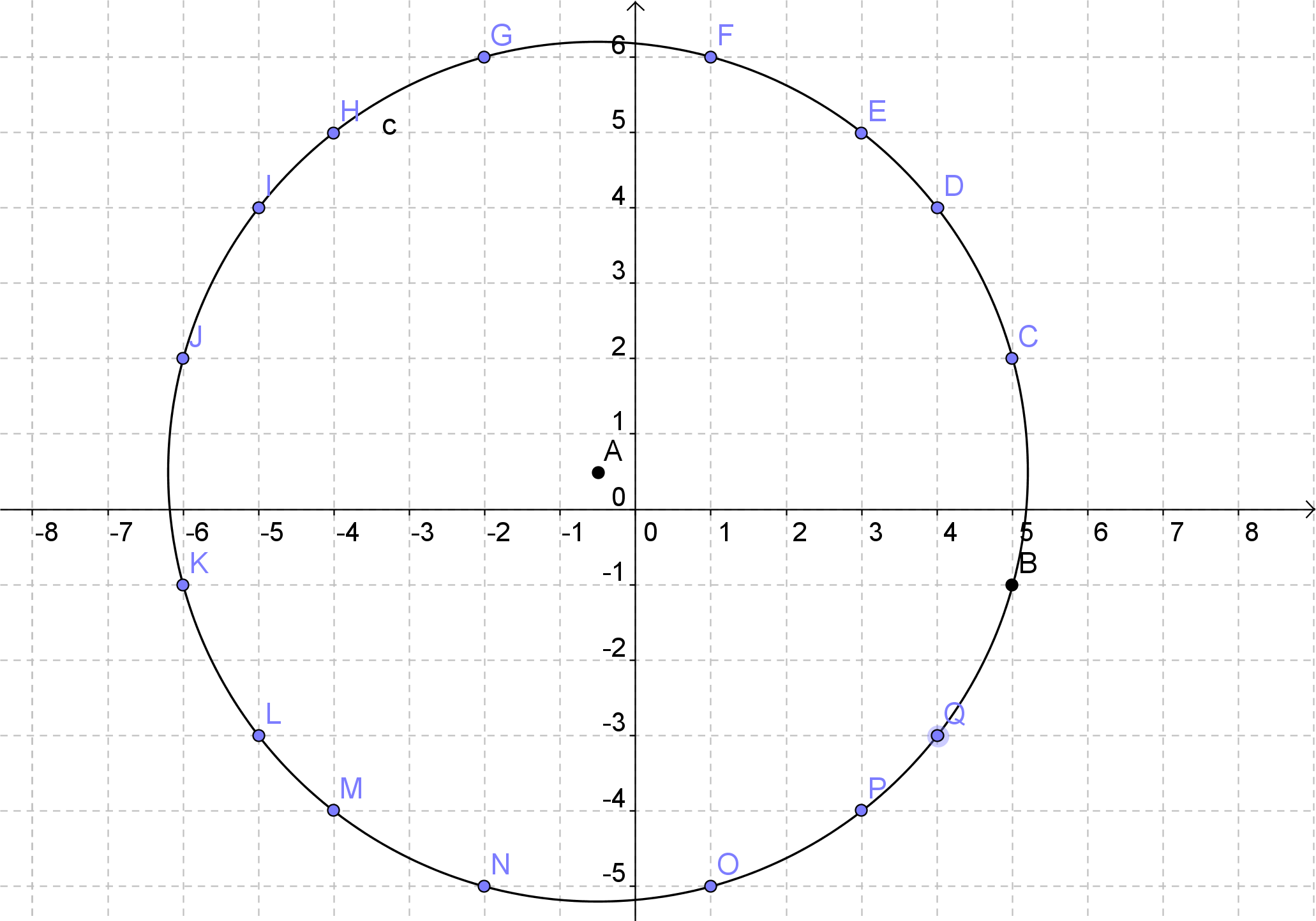
Pour preuve, les sommes de 2 carrés de 2 manières au moins ne sont pas nombreuses :
50 avec (1,7) et (5,5) est hors-jeu : On tombe sur une maille paire en partant de (1,1) mais sur seulement 12 points pour des raisons de symétrie du couple (5,5).
et le sera toujours...
65 avec (1,8) et (4,7) ne marche pas car les nombres ne sont pas de même parité donc les coordonnées ne sont pas "inversibles" selon les deux axes quel que soit le centre. On le retrouve dans la "fausse solution" en multipliant les coordonnées par 2, ce qui donne rac(260).
Idem pour 85 et 125...
Le plus petit valable est 130 avec les couples d'impairs (3,11) et (7,9) en partant donc de (1,1)
#19 - 15-07-2017 08:31:13
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteau 13
Le centre de la galette est un nœud , c'est presque trop évident mais bien sûr il faudrait une démonstration hmm
Je remets un peu de temps et je change la case réponse
La case réponse initiale étant fausse, et l'affirmation sur la position du centre également, je donne ma solution, sans accord de la nouvelle case réponse.
2R = 11.40 = 2[latex]\sqrt 32.05[/latex]
EDIT
Zappé "maille = 2 cm"
Il faut donc doubler la valeur trouvée, soit 22.80
#20 - 15-07-2017 09:26:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
gâtzau 138
Il est clair que tu as peu de chance d'être en accord avec la case réponse si tu proposes une valeur approchée du rayon 
Vasimolo
#21 - 17-07-2017 08:32:26
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
gâyeau 138
Ce gâteau m'intrigue. Le centre de la galette n"est-il plus un nœud ? Ou n'ai-je pas compris le post #17 ?
#22 - 17-07-2017 11:53:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gââteau 138
Dans l'énoncé initial on ne dit rien sur la position de la galette par rapport au quadrillage . La première idée est de centrer le quadrillage avec la galette mais ce n'est pas forcément la bonne 
Vasimolo
#23 - 18-07-2017 12:24:15
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1970
Gtâeau 138
J'ai trouvé 32,25 mais apparemment ça ne marche pas, donc il doit y avoir mieux...
Je suis parti du théorème des deux carrés de Fermat, pour trouver le plus petit nombre admettant 16 décompositions: c'est 5*13 = 65
En effet, on a 1²+8² = 4²+7² = 65, donc les 16 points suivants sont sur un cercle centré en O et de rayon sqrt(65) : (1;8),(-1;8),(1;-8),(-1;-8),(4;7),(-4;7),(4;-7),(-4;-7),(7;4),(-7;4),(7;-4),(-7;-4),(8;1),(-8;1),(8;-1),(-8;-1)
Rayon de racine(65) unités, avec un maillage à 2 cm et on veut le diamètre, ça nous donne 32,24903099 cm de diamètre, soit 32,25 mais pas glop. Je vais chercher mieux... Après tout, rien n'indique que le rayon est une racine d'entier
#24 - 18-07-2017 15:40:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâteua 138
Tu as eu la même idée que beaucoup , on peut faire mieux 
Vasimolo
#25 - 19-07-2017 09:26:52
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1970
gâteay 138
J'imagine. En passant en équation paramétrée, pour un rayon R et un centre (x0, y0), l'équation paramétrée du cercle est:
X = 2mR/(m²+1) + x0
Y = (m²-1)R/(m²+1) + y0
avec m un réel quelconque.
Il suffirait de trouver R, x0 et y0 (probablement tous irrationnels) qui donne 16 valeurs entières pour X et Y pour 16 m bien choisis. Pas simple...
|
 |

 Accueil
Accueil
 Forum
Forum