|
#1 - 04-06-2017 12:24:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 05-06-2017 15:10:44
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
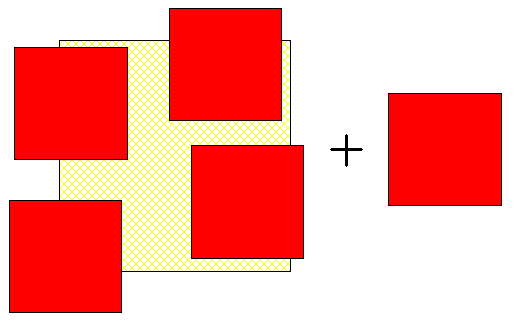
gâteay 134
Bonjour,
vraiment intéressant ce problème, la conjecture semble assez facile, mais c'est une autre paire de manche pour la démontrer...
Après avoir chercher à démontrer que l'on ne pouvait pas recouvrir le pourtour, je me suis aperçu que c'était en réalité possible avec un epsilon très petit (epsilon était Taille de la moitié du gâteau - Taille de la feuille )
En tout cas, il est possible de montrer sans trop de calculs que l'on ne peut pas recouvrir le pourtour avec seulement 4 feuilles, et qu'il y aura toujours au moins 1 petit bout sur l'un des côtés restant libre.
Il doit aussi être possible de montrer que si l'on cherche à recouvrir 3 des 4 côtés du pourtour complètemement, il y aura des très légères "fissures" qui s'éloigne suffisamment du centre (à plus du quart de la taille du gateau).
La 5eme feuille ne pourra donc pas recouvrir chacune de ces fissures + le bout restant sur le bord. Le même raisonnement s'applique à quelques détails près si l'on ne recouvre complètement que deux ou moins des côtés avec les 4 premières feuilles.
Je me rend bien compte que ce n'est vraiment pas clair, je vais essayer de faire un figure, si je ne suis pas trop flemmard, pour expliquer mon propos...
Edit:
Voila une image, j'ai un peu triché pour que ça montre ce que je voulais, car ça ne marche que si epsilon est vraiment très petit.
Les 4 premières feuilles sont les rouges, on voit bien que les fissures entre chacune des feuilles deviennent de plus en plus grande. La cinquième feuille (en vert) ne pourra jamais recouvrir tout le reste.
Pour démontrer que l'on ne peut pas recouvrir le pourtour avec 4 feuilles, il suffit de montrer qu'une feuille ne recouvrira jamais plus de 2x la moitie de la taille du gateau, ce n'est pas très dur...

Si il y a une démo propre (et si possible plus simple), je serai très curieux...
#3 - 05-06-2017 17:35:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 134
Bonsoir Caduk 
Je pense avoir une explication simple . Tu es sur la bonne voie mais il te manque quelques éléments .
Vasimolo
#4 - 05-06-2017 23:04:33
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Gtâeau 134
Doit-il accepter l'offre sachant que les feuilles peuvent être orientées n'importe comment , se chevaucher , déborder du gâteau mais ne jamais être découpées ?
De la manière dont est posée la question, je suppose que "Oui", mais je suppose aussi que cette réponse ne te suffit pas  . .
Si c'est le cas, je ne vois pas trop d'autres possibilités de placer ces feuilles autrement qu'ainsi :
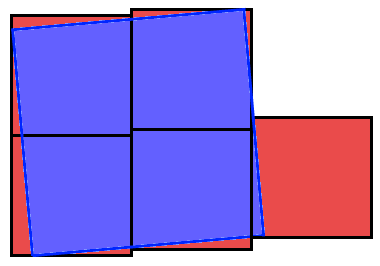
Il faudrait ensuite pour le montrer, calculer le pourcentage minimum que doivent faire les cotés des feuilles par rapport à celui du gâteau.
Mais cela me paraît un calcul assez difficile qui risque de me demander trop de temps  ... ...
Et venez nombreux , ici ou ailleurs ( le forum est un peu triste en ce moment )
Je suis bien d'accord, et c'est pour cela que je suis là  ! !
Je trouve que l'élite de P2T a un peu déserté le navire ces dernier temps, et qu'on se retrouve bien seuls à essayer de le maintenir à flot  . .
#5 - 06-06-2017 14:16:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 134
@Jack : j'ai bien peur que ta construction ne couvre pas l'ensemble du carré 
Vasimolo
#6 - 06-06-2017 17:41:58
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
#7 - 06-06-2017 18:01:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#8 - 07-06-2017 09:02:33
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâtzau 134
Je sèche : ça a l'air impossible, mais comment le démontrer ?
On peut déjà remarquer que si on considère les 4 coins et le centre du gâteau, ces 5 points doivent appartenir à 5 feuilles différentes. Après, j'ai essayé de considérer les points du contour du gâteau, mais je n'ai pas réussi à aboutir.
#9 - 07-06-2017 12:11:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#10 - 07-06-2017 18:13:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gtâeau 134

Chaque carré ne peut contenir qu'un seul point bleu,
donc, chacun en contient exactement 1.
Le carré « central » contient, au plus, 1 point vert , associé à un des 4 coins
et dans ce cas, pas plus de 2 points jaunes.
Si, dans un coin, aucun point vert n'est recouvert par le carré central,
ils ne peuvent l'être que par le carré situé dans ce coin.
Ce carré doit donc contenir l'intégralité des deux segments rouges.
Mais dans ce cas, il ne pourra contenir qu'un seul point jaune.
Conclusion :
Si le carré central contient un point vert,
on arrive à un total maximum de 7 points jaunes recouverts. Impossibilité.
Si le carré central ne contient pas de point vert, il doit contenir 4 points jaunes
qui sont obligatoirement les 4 points « centraux ».
Seulement, dans ce cas, il ne participe pas à recouvrir le périmètre de la figure
qui sera strictement inférieur à 16 segments rouges. Impossibilité.
#11 - 07-06-2017 18:42:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 13
C'est bien vu Gwen et très malin comme d'habitude 
On peut éviter l'étude de tous ces cas en diminuant le maillage mais il faut passer par une étape intermédiaire qui est masquée par tes points jaunes et verts .
Le trop plein d'astuces cache un peu la clé du problème , je prends quand même .
Je savais qu'on y arriverait 
Vasimolo
#12 - 07-06-2017 22:43:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
âGteau 134
Oui, j'ai la même avec 9 points...
Un coin = un milieu des côtés, un seul.
Le centre, idem.
Mais dans ce dernier cas, le coup du périmètre coince un peu...
Chaque milieu des côtés exclut un point jaune central "différent" et donc on aboutit à une contradiction pour que le carré central touche le milieu d'un côté, mais c'est plus facile à intuiter qu'à démontrer.
#13 - 08-06-2017 16:18:41
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâetau 134
J'ai trouvé une méthode basée sur tes indications, mais elle n'est pas très élégante. Elle nécessite l'étude de nombreux cas (études que je passe sous silence, mais que je peux expliquer si nécessaire).
Tout d'abord, on recouvre le gâteau par un réseau de 25 points comme ci-dessous. Le gâteau est supposé de côté 2, aussi la distance entre deux points voisins vaut 0,5.

Ensuite, on démontre un lemme affirmant qu'aucune de ces 3 figures ne peut être contenue dans un carré de côté strictement inférieur à 1 :

À l'aide de ce lemme, on cherche à répartir les 25 points en 5 ensembles, chaque ensemble devant être recouvrable par un carré de côté <1. En étudiant quelques cas, on aboutit à ce que la seule répartition possible (à symétrie près) est celle que l'on visualise avec les couleurs de la première figure.
Or cette répartition ne convient pas, car du fait de la position des points orange, la feuille carrée qui recouvre les points orange ne peut toucher le tour du gâteau ; et comme chacune des 4 autres feuilles carrées ne peut recouvrir que strictement moins de 2 unités du périmètre du gâteau qui vaut 8 unités, on ne peut recouvrir tout le gâteau de cette manière.
#14 - 08-06-2017 17:49:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
#15 - 09-06-2017 16:30:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 1334
Des idées assez proches pour Gwen et Ebichu 
J'étais parti sur idée différente :

Une feuille de côté inférieur à 1 posé sur un des angles du gâteau de côté 2 va recouvrir une longueur inférieure à 2 sur l'ensemble des lignes noires . La dernière feuille ne pourra donc jamais recouvrir le reste .
Vasimolo
#16 - 09-06-2017 17:04:55
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâtezu 134
Avec uniquement l'argument du périmètre, tu te trompes. Couvrir tout le périmètre est parfaitement possible.
Ta conclusion semble être un superbe raccourci...
#17 - 09-06-2017 17:26:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 1344
Je n'ai pas donné la solution mais l'idée 
Attention les lignes noires sont constituées des côtés mais aussi des médiatrices des côtés du carré .
Vasimolo
#18 - 10-06-2017 07:56:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteeau 134
Effectivement, chaque carré est lié au centre ou à un coin.
Dans un coin, pas plus de 2 traits recouverts (en terme de longueur) et au centre pas plus de 2 rac(2).
10,8 < 12 c'est donc impossible.
#19 - 11-06-2017 10:06:39
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Gâteu 134
Doit-il accepter l'offre sachant que les feuilles peuvent être orientées n'importe comment , se chevaucher , déborder du gâteau mais ne jamais être découpées ?
Finalement, la réponse est non ! Je commençais à m'en douter  ! !
Mais je suis très déçu. J'espérais que tu avais une solution miracle à proposer.
En tout cas merci de participer car je sais que tu préfères largement les petites promenades hexagonales à la consommation d'indigestes gâteaux.
Pour te montrer que je sais faire autre choses que des promenades hexagonales, je me suis lancé dans une énigme mathématique :
http://www.prise2tete.fr/forum/viewtopic.php?id=13412
J'espère que tu me montreras que tu sais faire autre chose que des gâteaux  ! !
#20 - 11-06-2017 18:02:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
|
 |

 Accueil
Accueil
 Forum
Forum