|
#1 - 20-05-2017 23:20:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 21-05-2017 11:25:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 1331
Salut Vasimolo.
J'ouvre avec un minimum à 42,7846...cm.
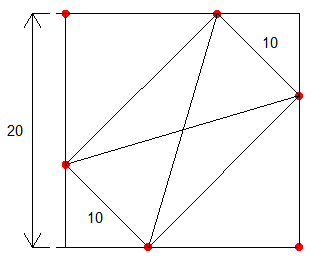
Obtenu en plaçant 1 point à chaque coin et les 2 autres points placés sur une diagonale, symétriquement par rapport au centre. Dans cette config, il y a 3 triangles possibles à regarder:
-1) Prendre 2 points de coin d'un même coté et le point le plus proche de la diagonale
-2) Prendre un point de coin de la diagonale et les 2 points de la diagonale (on suppose qu'ils ne sont pas alignés)
-3) Prendre les 2 points de la diagonale et un point de coin hors diagonale.
La meilleure solution est obtenue quand 1) et 2) sont égaux, et après vérification que 3) n'est pas plus petit.
Dans ce cas, le point de la diagonale est situé à 0,3446... ( x 20 cm) du coin le plus proche (résolution d'une équation de second degré).
#3 - 21-05-2017 15:33:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteeau 131
Mmh... pas évident ces problèmes.
J'ai une disposition qui, dans un carré de côté 1, nécessite [latex]\frac{3+\sqrt{2}}{2}[/latex] de coulis, soit environ 44,14 cm. As-tu trouvé mieux ? Connais-tu la solution ?
#4 - 21-05-2017 17:23:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Gâtea u131
J'arrive à 44,142135... cm
#5 - 21-05-2017 17:56:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâeau 131
Bonjour à tous 
@Nodgim : On peut faire pire .
@Gwen et Ebichu : vous avez le même résultat , j'ai aussi cette disposition dans mes brouillons : est-on assuré que c'est la pire ?
Pour répondre à Ebichu , je n'ai pas de réponse au problème . Il entre dans la catégorie de ceux que j'affectionne particulièrement avec un énoncé simplissime et une recherche extrêmement ouverte . J'ajoute qu'il s'agit d'un problème original et que la solution peut être très complexe ( voire trop ) pour de simples joueurs comme nous .
Je peux bien sûr lever le masque si chacun y trouve son compte même si je trouve le challenge assez amusant .
Bonne recherche 
Vasimolo
#6 - 21-05-2017 18:08:19
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gâteua 131
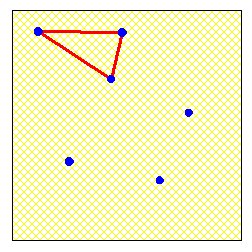
Bonjour, j'ai pas trop de temps en ce moment pour y réfléchir, mais à première vue, ce placement me semble pas mal:
repere orthonormé:
(0,0) (0,1) (0.21464, 1/2) (0.78536, 0) (0.78536,1) (1, 1/2)
Et on trouve une longueur de coulis de 41.7649 cm mais peut être peut on trouver plus long
#7 - 21-05-2017 18:11:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteu 131
@caduk : on peut faire pire 
Vasimolo
#8 - 23-05-2017 18:16:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
âGteau 131
Un indice 
Ne pas remplir les quatre coins .
Vasimolo
#9 - 23-05-2017 20:21:18
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
fâteau 131
J'attendais tranquillement la soluce, mais ton dernier message m'a fait regarder à nouveau ce problème.
Il semble bien qu'il y a une config à 44,14...cm : 2 points dans les coins d'une diagonale, les 4 autres points sur le périmètre également, mais à 0,35...(*20 cm)
des 2 coins de l'autre diagonale.
Tu te demandais si on pouvait prouver qu'il n'y a pas mieux. Pas simple, mais déja, on peut dire qu'il y a au moins 3 points sur le périmètre (car on peut toujours zommer sur une figure sans points sur le périmètre ). Par ailleurs, il y a un minimum de symétrie à respecter, car l'optime est obtenu par égalités. ça réduit tout de même pas mal les possibilités.
#10 - 23-05-2017 20:47:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâeau 131
C'est ça Nodgim 
Je suis quasi-convaincu que c'est la meilleure solution , il reste à trouver une justification simple .
Vasimolo
#11 - 23-05-2017 22:41:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#12 - 24-05-2017 15:51:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâteai 131
@nodgim : je ne comprends pas bien, pourquoi la solution aurait-elle des symétries ?
Sinon, pour restreindre le champ des possibles, une idée qui raffine celle de nodgim.
Considérons l'enveloppe convexe de nos 6 sommets (=mûres). Considérons ensuite les deux segments de l'enveloppe convexe dont une extrémité est ce sommet, et traçons les deux perpendiculaires à ces deux segments passant par ce sommet. Ces deux perpendiculaires délimitent 4 domaines, dont un domaine n'a que ce sommet en commun avec l'enveloppe convexe (le domaine le plus "extérieur"). Si on déplace ce sommet ailleurs dans ce domaine, alors sa distance aux 5 autres sommets augmente.
On peut donc supposer que les sommets de l'enveloppe convexe sont situés sur le carré.
Autre remarque utile, plus simple : on ne peut pas avoir 3 mûres sur le même côté du carré, car sinon 40 cm de coulis suffisent.
#13 - 24-05-2017 18:17:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtzau 131
Pour ce qui est des symétries , on peut noter que dans la solution proposée , il y a exactement un point dans chaque secteur limité par les axes de symétrie du carré .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum