|
#1 - 09-06-2018 19:46:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 10-06-2018 12:39:59
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâtteau 152
Bonjour.
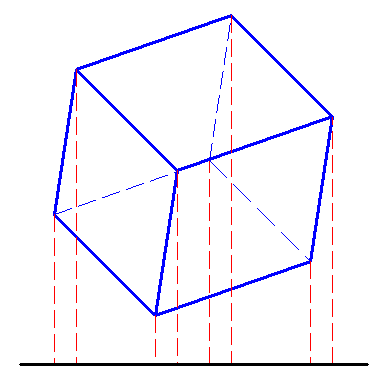
Ce cube doit logiquement posséder une arrête de longueur :
a=10.√21
#3 - 10-06-2018 15:01:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteua 152
Salut Vasimolo,
oui, c'est possible (et c'est joli).
Voici les coordonnées de 8 sommets qui fonctionnent :
A(0 0 10)
B(20V5 0 20)
C(18V5 4V105 40)
D(-2V5 4V105 30)
E(-4V5 -2V105 50)
F(16V5 -2V105 60)
G(14V5 2V105 80)
H(-6V5 2V105 70)
J'ai trouvé ça analytiquement : après avoir posé A(0 0 10), on pose B(x 0 20).
L'angle droit en BAD, la relation AB=AD et zD=30 permettent d'exprimer xD et yD en fonction de x.
On fait pareil avec E, et on tombe sur une équation bicarrée qui permet de trouver x=20V5. Tout le reste s'en déduit.
#4 - 10-06-2018 17:41:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gteau 152
Bonnes réponses de Unecoudée et Ebichu
C'est un peu calculatoire mais le jeu en vaut la chandelle 
Vasimolo
#5 - 10-06-2018 19:38:11
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâtaeu 152
Tiens ! Ma réponse de ce matin n'est pas passée....
Je disais que là j'assurais le service minimum....
La réponse est oui, et ça se montre sans calcul.
Tout d'abord, pas de changement si au lieu de 10, 20,....80, on prend 0,1,2,...7. C'est à dire si le point le plus bas touche le sol plan et qu'on divise les valeurs par 10.
On regarde seulement la base du cube, le carré du bas. On suppose le sommet diagonalement opposé au sommet le plus bas à la hauteur 3, supposition justifiée à partir d'une dimension minimale du coté du cube. Si les 2 sommets de la seconde diagonale sont à la même hauteur, alors ils sont à 1,5. Il est évident qu'en pivotant ce carré selon l'axe 1ère diagonale, les 2 sommets de la 2ème diagonale vont voir leur hauteur respective, du fait de la symétrie, varier de la même valeur, l'un vers le haut, l'autre vers le bas. Aussi, on ne peut manquer d'obtenir 1 pour l'un et 2 pour l'autre (1,5 + - 0.5).
Voila donc déjà les valeurs 1,2 et 3 atteintes. Celles ci peuvent être atteintes pour n'importe quelle longueur de coté du cube, à condition bien sûr d'un minimum. Pour un coté de longueur 3, ça marche déjà, avec la 1ère diagonale de la base inclinée à 45°. Bien entendu, pour cette valeur, le sommet le plus bas du carré du haut est inférieur à la hauteur 4. Or, on a dit que, au dela de ce minimum, on savait obtenir 1,2, et 3 pour les 3 sommets les plus bas. On peut donc obtenir toutes les valeurs continues de la hauteur du sommet le plus bas du carré du haut à partir d'une valeur inférieure à 3. On peut donc obtenir 4. Et ensuite, les 2 carrés étant inclinés de la même façon, on obtient immédiatement les valeurs 5,6 et 7 pour les 3 autres sommets.
#6 - 11-06-2018 09:14:05
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
hâteau 152
Bonjour,
Soit C le coté de la boite et a et b les angles d'inclinaison/horizontale.
On peut ecrire que c = 20/sin(a) = 10/sin(b) .
Il suffit que le coin le plus bas soit à 10cm du sol que au moins un des angles soit inférieur à 30 degrés et que le coté soit > à 10 cm.
@+
#7 - 11-06-2018 18:36:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 52
@Nodgim : oui , ça marche , tu as essayé de trouver la valeur de l'arête ?
@Bastidol : c'est un bon début mais avec c quelconque les quatre sommets restants risquent de ne pas avoir la bonne altitude .
Vasimolo
#8 - 11-06-2018 22:42:06
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Gâtteau 152
Les coins diagonalement opposés du carré inférieur du cube sont respectivement aux altitudes 10 + 40 et 20 + 30; ceux du carré supérieur à 50 + 80 et 60 + 70.
Dans le sens d'un des deux rectangles diagonales c x cV2, les arêtes verticales du cube se décalent de (40-10)/V2 = 15V2; dans l'autre de (30-20)/V2 = 5V2
Au final, ce décalage est de: V[(15V2)²+(5V2)²] = 10V5
L'arête c du cube est donc telle que: V(c²-500) = 40, soit c = 10V21, sans garantie 
#9 - 12-06-2018 00:35:05
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Gteau 152
Dans le repère orthonormé (A,B,D,E), on construit le cube ABCDEFGH.
Dans ce repère, un plan P quelconque peut avoir une équation de la forme ax+by+cz+d=0, avec a²+b²+c²=1 et d>=0.
Soit d(M,P) la distance d'un point M(xM,yM,zM) à P, on a d(M,P)=|axM+byM+czM+d|/rac(a²+b²+c²)=|axM+byM+czM+d|.
En prenant a=d, b=2d et c=4d, on a :
d(A,P)=|d|=d
d(B,P)=|a+d|=2d
d(C,P)=|a+b+d|=4d
d(D,P)=|a+d|=3d
d(E,P)=|a+c|=5d
d(F,P)=|a+c+d|=6d
d(G,P)=|a+b+c+d|=8d
et d(H,P)=|a+c+d|=7d
On a dans ce cas a²+b²+c²=d²+(2d)²+(4d)²=21d², donc d=1/rac(21) en unité de longueur du repère, c'est-à-dire la longueur L de l'arête du cube.
On veut d=10cm, soit L/rac(21)=10cm. D'où L=10rac(21) ~ 45,8cm
Donc en prenant un cube d'arête L=10rac(21) et en l'orientant "comme il faut", on peut avoir les 8 sommets à des altitudes régulièrement espacées de 10 à 80cm.
Merci pour ce problème sympa.
#10 - 12-06-2018 08:23:14
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
Gâetau 152
Bonjour,
......et que le sinus d'un angle soit le double de celui de l'autre.
Si l'arête avait été donnée on aurait pu faire le calcul .
@+
#11 - 12-06-2018 08:57:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
fâteau 152
Le coté du cube vaut 10V21 si je ne me suis pas trompé. Calcul relativement simple si on a posé les 3 bonnes équations de départ....
#12 - 12-06-2018 11:14:41
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
#13 - 12-06-2018 15:24:44
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 15
Bonjour,
Ton pâtissier a raison.
En posant :
sq5 = sqrt(5); sq21=sqrt(21)
Voici par exemple les coordonnées des sommets d'un cube qui répond au problème, de côté 10*sq21 = 45.83 cm.
#14 - 12-06-2018 22:59:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâteay 152
@Dylasse : oui .
@Bastidol : Tu dois pouvoir trouver l'arête .
@Nodgim : oui .
@LeJeu : Je n'ai pas compris autour de quel axe tu tournes 
@Enigmatus : oui , les calculs peuvent être faits aisément à la main .
Bon courage à ceux qui cherchent encore 
Vasimolo
#15 - 13-06-2018 08:59:07
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
Gâteau 512
Bonjour,
Oui en effet.
arête = 40/cos(a) = 20 /sin(a) = 44,7 Cm
@+
#16 - 13-06-2018 14:15:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 152
Non Bastidol , il faut creuser un peu plus 
Vasimolo
#17 - 13-06-2018 15:47:22
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
Gâteauu 152
Bonjour Vasimolo,
Je vois que me dessins ne font pas impression .... du coup sur la même idée , je me lance dans le calcul du coté du cube, quitte à être privé de gâteau , autant prendre des risques :-)
pour un cube de coté 1:
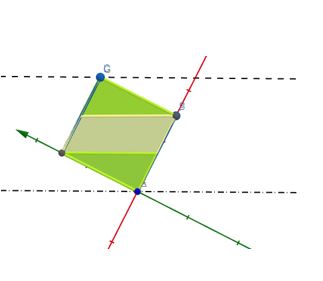
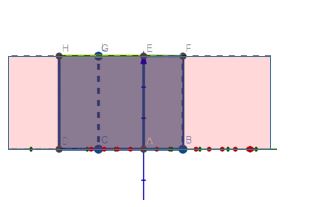
Je reprends ma vue de dessus et dessine l'axe Delta de rotation
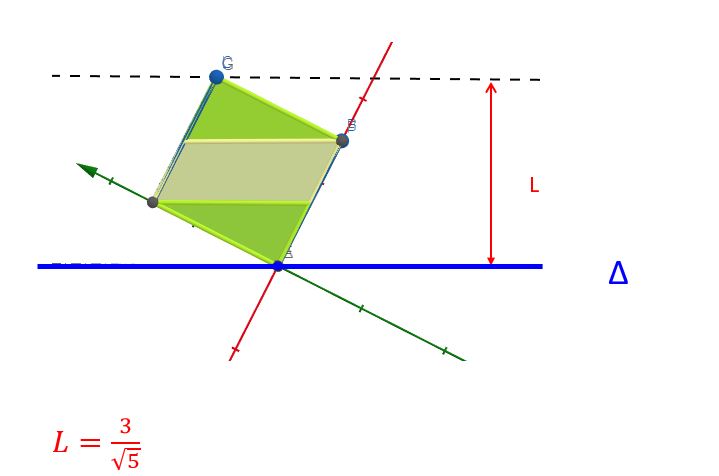
Et j'exprime qu’après rotation autour de Delta la hauteur du point C doit arriver au trois quart de la hauteur du point E
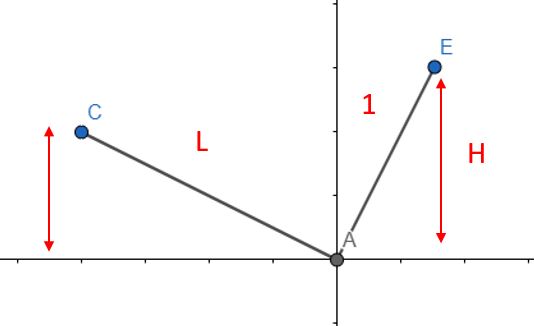
Soit L* sin(a) = 3/4 * cos(a)
avec L = 3/racine(5)
soit tan(a) =racine(5) /4
et donc H = cos(a) = 4 /racine(21)
Dans le problème cette hauteur vaut 40 cm ,
le coté du cube est donc 10 Racine(21)
#18 - 13-06-2018 17:10:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 152
Si j'ai bien compris , on tourne autour d'un axe Δ contenu dans le plan de la face supérieure . Je ne pense pas que ça marche , en tout cas la valeur que tu donnes n'est pas la bonne 
Pas facile de suivre les déplacements des sommets d'un cube dans l'espace 
Vasimolo
#19 - 13-06-2018 18:05:06
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
Gâteau 1152
Merci de ta relecture, Vasimolo, je retourne à mes fourneaux donc ....
#20 - 14-06-2018 07:44:07
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
Gâteau 1552
dernière fournée....
après relecture j'ai corrigé le calcul du cos à partir de la tg .... ( le 41 est devenu 21)
Mais j'imagine que je dois être à coté de la plaque car tu as l'air de douter fortement de la méthode utilisée ....
#21 - 14-06-2018 08:57:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 52
On peut trouver des cubes à arête entière dont toutes les hauteurs sont entières.
Exemple : un cube d'arête 18 avec les hauteurs 0, 2, 8, 10 , 16, 18, 24, 26.
#22 - 14-06-2018 18:25:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 152
@LeJeu : oui c'est bon 
@Nodgim : oui , c'est facile à faire par exemple avec un triplet pythagoricien abc , un entier d et une petite bascule du plan vert .
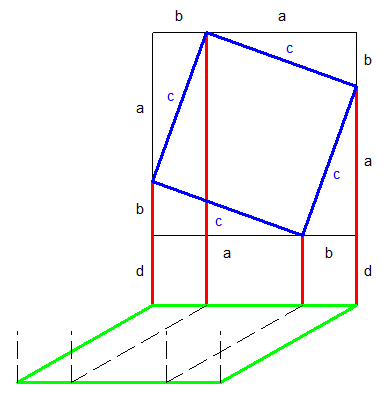
Vasimolo
#23 - 17-06-2018 12:00:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 152
Un grand merci à tous les participants 
Le jour je ne m'émerveillerai plus devant ces petits problèmes , je laisserai tomber les maths et tout le reste .
Personnellement j'étais passé par les coordonnées , ce n'est pas très élégant mais très efficace .
A bientôt pour un prochain gâteau 
Vasimolo
#24 - 17-06-2018 18:21:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâetau 152
Une autre approche que les coordonnées :
A = sin a x V2, A est le sommet le plus haut du carré du bas. (A= 3 )
B = cos a sin b x V2/2 est un décalage par rapport à A/2. (B = 1/2 )
C = cos a cos b x, C étant le point le plus bas du carré du haut. (C = 4 )
x étant la longueur de l'arête.
On trouve facilement que x = V((A² + 4B² + 2C²)/2)
Et on peut aussi facilement trouver des valeurs de x entières avec les 8 hauteurs de sommets entières et distinctes.
J'espère, Vasimolo, que tu te ne lasseras jamais de ces petits problèmes, ce serait dommage.
|
 |

 Accueil
Accueil
 Forum
Forum