|
#1 - 27-11-2011 18:26:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 27-11-2011 20:17:44
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
Gââteau 46
Désolé Vasimolo, mais pour l'instant pas (encore) d' "impair" au terrier 

#3 - 27-11-2011 22:55:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gtâeau 46
Ce n'est pas grave , continue à creuser 
Vasimolo
#4 - 27-11-2011 23:26:32
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Gâteua 46
Effectivement c'est impossible  , d’ailleurs la forme du gâteau n'a pas d’importance, pourvue que les bords ne soient pas en biais. , d’ailleurs la forme du gâteau n'a pas d’importance, pourvue que les bords ne soient pas en biais.
La preuve :
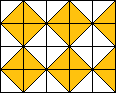
On quadrille le gâteau en carré : chaque carré est soi plain (pièce carré) soi coupé en diagonale (une pièce triangulaire un parallélogramme chevauche le carré).
Chaque carré coupé en diagonale est voisin d'un autre carré coupé en diagonale.
En partant d'un carré "en diagonale", de voisin en voisin on construit un parcours.
On fini nécessairement par retomber sur un carré de notre parcours. Et c'est forcément le premier (les autres sont déjà recouvert entièrement par le parcours)
Le parcours est donc un circuit fermé qui tient sur des carrés : il y a donc un nombre pair de carré (autant à l’allée et au retour dans chaque sens) puis un nombre pair de pièce dans le circuit.
Circuit dans le gâteau exemple :

En éliminent les pièces du circuit, on obtient un nouveau gâteau constitué du même type de pièce.
Tant qu'il restes des pièces triangulaire ou parallélépipédique, on peut trouver un nouveau circuit.
La preuve n'est pas finie, il reste à prouver que dans chaque circuit il y a autant de triangles que de parallélépipèdes.
Pour cela on va différencier carrés à diagonale / et les carrés à diagonale \
_Quand on passe de / à \ (ou l'inverse) la pièce de jonction est un triangle.
_Quand on passe de / à / (ou \ à \) la pièce de jonction est un parallélogramme.
Dans l'exemple ci dessus le circuit s'écrit : \ \ / / \ \ \ / / /
On raisonne par récurrence : Supposons qu'un circuit qui s'écrive avec 2n "/" et "\" contienne toujours un nombre pair de chaque pièce.
Prenons un circuit quelconque de 2(n+1) "/" et "\"
On va retirer deux slash consécutifs, puis voir comment le nombre de chaque type de pièce est modifié en fonction des slash voisins : il y a 2^4=16 cas à considérer, que l'on peut réduire à 5 avec les symétries verticale et horizontales :
1) / / \ \ --> / \ 2 parallélogrammes de disparus
2) / \ / \ --> / \ 2 triangles de disparus
3) / / / / --> / / 2 parallélogrammes de disparus
4) / / \ / --> / / 2 triangles de disparus
5) / \ \ \ --> / \ 2 parallélogrammes de disparus
donc par récurrence il y a bien un nombre pair de chaque type de pièce dans le circuit de 2(n+1) pièce, et le résultat est démontré.
Résumé pour les faignant  : On peut retirer au gâteau des circuit comportant un nombre pair de pièce triangulaires et parallélépipédique jusqu'à ce qu'il ne reste plus de telles pièces, il y en donc un nombre pair de chaque type. : On peut retirer au gâteau des circuit comportant un nombre pair de pièce triangulaires et parallélépipédique jusqu'à ce qu'il ne reste plus de telles pièces, il y en donc un nombre pair de chaque type.
Merci aux lecteurs 
Mathieu
#5 - 27-11-2011 23:34:37
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Gâteu 46
J'ai oublier l'initialisation dans ma récurrence.
Et là je vais faire quelque chose de surprenant  , je vais initialiser avec des circuit impossible (à deux slash). , je vais initialiser avec des circuit impossible (à deux slash).
Je peux le faire puisque je me suis détaché de certaines contrainte de la figures.
Par extension, (quand il y a assez de slash) le résultat reste vrai pour le gâteau.
cas 1 : / / 2 parallélogrammes (il ne faut pas oublier de boucler le circuit)
cas 2 : / \ 2 triangle
les autres cas sont identiques à symétries près.
Voilà 
Mathieu
#6 - 27-11-2011 23:36:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#7 - 27-11-2011 23:39:18
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Gâtea 46
Non non tout y est 
#8 - 27-11-2011 23:44:13
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
#9 - 28-11-2011 01:43:57
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Gtâeau 46
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#10 - 28-11-2011 15:41:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteauu 46
@Mathieu : j'ai sûrement de la fumée dans les yeux mais je ne vois pas pourquoi sur chaque circuit le nombre de carrés ou de pièces serait pair ?
Vasimolo
#11 - 28-11-2011 17:53:43
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Gâteau 64
Je vais développer mon indication pour montrer qu'il y a toujours un nombre pair de carré dans un circuit : autant à l’allée et au retour dans chaque sens
Je précise que je parle d'un circuit constitué uniquement de carré. Ces carrés sont recouverts par des triangles et des parallélogrammes. Ils sont de la même dimension que les carrés du nappage, mais à cheval entre deux pièce.
Différencions les carrés en quatre groupes suivant la direction du prochain carré dans le circuit : au dessus, en bas, à droit ou à gauche
Notons h,b,d et g le nombre de carrés respectifs ces ensembles.
Puisque que, par définition, le circuit revient à sont point de départ les déplacements suivant chacun des axes (haut-bas et droite-gauche) s'annulent.
Autrement dit : h=b et d=g donc h+b+d+g=2(h+d)
Il y a donc un nombre pair de carré.
Or chaque pièce est constitué d'exactement 2 demi carré, il y a donc autant de pièce que de carré dans le circuit : un nombre pair.
Mathieu
#12 - 28-11-2011 19:37:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 46
D'accord pour ce point 
Tu peux expliquer ta récurrence , je ne vois pas comment tu élimines les pièces 
Vasimolo
PS : Ne te décourage pas Azdod , on peut faire très simple avec un peu d'astuce .
#13 - 28-11-2011 23:11:26
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Gâteauu 46
Détails de la récurrence :
Insistons d'abord sur le fait que la forme d'une pièce (non carré) dépend uniquement des orientation différentes (triangle) ou des orientations identiques (parallélogramme) des deux diagonales des carrés qui la recouvre.
On élimine donc la notion de position spatiale pour ne raisonner que sur des circuits plus généraux, où seul l'ordre d'enchainement des carrés compte. (Un peut comme quand on démontre un résultat sur les nombres réels en passant par les nombre complexes)
On représentes donc ces circuit par une suite des slash représentant le sens de la diagonale des carrés, sens oublier qu'après le dernier slash, on revient au début :
\ \ / / \ \ \ / / / pour l'exemple de l'énoncé.
Pour ces circuits (et donc pour les circuits réels sur le gâteau par extension) on montre par récurrence que si ils ont un nombre pair d'éléments, alors ils ont un nombre pair de chaque type de pièce.
Remarquons enfin qu'une symétrie horizontale (exemple : / / / \ devient \ \ \ / ) ou verticale (exemple : / / / \ devient / \ \ \ ) ne change pas le nombre de chaque type de pièce. Car seul l'égalité (/ / parallélogrammes) ou la différence (/ \ triangle) compte pour la pièce entre deux slash, et ces symétries ne changent pas cette propriété.
J'ai déjà fait au 2ème post l’initialisation de la récurrence pour n=2.
Si le résultat est vrai pour tout circuit de 2n carrés,
alors en éliminant deux carrés consécutifs d'un circuit de 2(n+1) carrés, il suffit de recoller les bout à bout pour obtenir un circuit de 2n carré, et on peut alors appliquer l'hypothèse de récurrence (nombres pairs).
Il reste à montrer que en éliminant les deux carrés, on a bien modifié chacun des nombre de triangle et de parallélogramme d'un nombre pair.
La suite est détaillé dans le 1er post, je précise juste la notation en colorant en rouge les carrés (slash) éliminés:
/ / \ / devient / /
que je notais plus simplement / / \ / --> / /
Les carrés voisins qui encadrent les deux éliminés sont représentés pour pouvoir faire les déductions sur la forme des pièces.
@Vasimolo en me demandant sans arrêt des précisions,
tu n'est pas loin de tuer ma passion 
Mathieu
#14 - 28-11-2011 23:26:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 6
Pas d'inquiétude Mathieu , je lis tes messages avec attention mais j'aime bien tout comprendre 
Je suis chiant mais attentif à ceux qui me font le plaisir de répondre à mes énigmes 
Bref je vais passer ta réponse au peigne fin dès demain .
Vasimolo
#15 - 29-11-2011 19:02:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gtâeau 46
D'accord Mathieu , ça marche bien et c'est plutôt astucieux  . La couleur rend plus visibles les carrés et slashs supprimés . . La couleur rend plus visibles les carrés et slashs supprimés .
Pour les autres , il existe une démonstration très expéditive , avec des coloriages justement .
Vasimolo
PS : J'ai ajouté un petit indice pour ceux qui ne trouvent pas d'angle d'attaque 
#16 - 29-11-2011 22:40:02
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
#17 - 29-11-2011 22:44:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
hâteau 46
Bien joué Mathieu , on a le même dessin même s'il y en a d'autres !!!
Vasimolo
#18 - 30-11-2011 16:26:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteua 46
J'ai ajouté un nouvel indice .
Vasimolo
#19 - 30-11-2011 18:09:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteeau 46
Il me semble que pour les parllélogrammes, le nombre impair est atteint pour un rectangle avec une dimension paire*impaire.
Exemple :2*1.
#20 - 30-11-2011 19:02:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 4
Je ne pense pas Nodgim , avec un rectangle 2X1 je vois mal autre chose que deux parts carrées .
Vasimolo
#21 - 01-12-2011 19:09:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
fâteau 46
Bon apparemment seul Mathieu s'en est sorti ( avec 2 démos tant qu'à faire ) , je vous laisse lire les solutions 
Le coloriage peut paraître artificiel mais , dans ce type de problèmes , c'est plutôt routinier et extrêmement efficace .
Merci à tous pour la participation et à bientôt pour un prochain gâteau 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum