Enigme Gâteau 13 @ Prise2Tete

Vasimolo · #1

Et on poursuit la série

Notre apprenti calamiteux a bien trop fait cuire le quatre quarts que je lui ai commandé . Profitant de l'absence de son patron , je lui fait remarquer que le bord du gâteau se sent un peu mal . Voulant bien faire , il s'empare d'un couteau et commence à 'enlever les parties incriminées . Les pas de son chef dans son dos lui font quelque peu massacrer la fin du travail et voilà la bête :

Mais quel était donc le rayon du gâteau ????

Vasimolo

Pour ceux qui veulent une démonstration "à la main" :

Indice :Spoiler : [Afficher le message] Ptolémée

McFlambi · #2

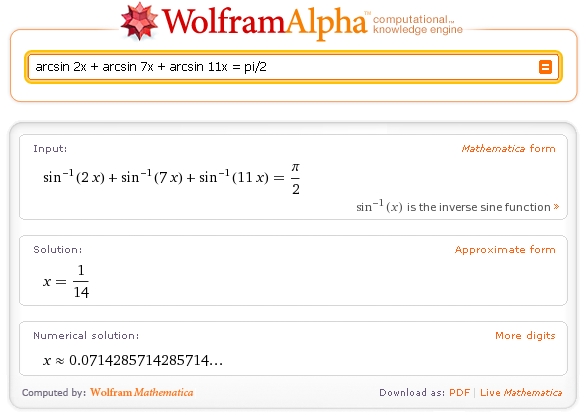
étant donné les doublons, je me place sur un demi cercle, avec 3 segments de 4, 14 et 22cm qui le partagent.

Il y a donc 4 points, disons A,B,C,D
de coordonnées :

$A(-r,0),\quad B(r \cos x, r \sin x),\quad C(r \cos y, r \sin y),\quad D(r,0)$
avec

$AB = \sqrt{r^2 {(\cos x +1)}^2+r^2 \sin^2 x}= r \sqrt{2(1+\cos x)}=4$

$BC = r \sqrt{{(\cos y - \cos x)}^2+{(\sin y - \sin x)}^2} = r \sqrt{2(1-\cos x \cos y - \sin x \sin y)} = r \sqrt{2(1-\cos(y-x))}=14$

$CD=r\sqrt{{(1-\cos y)}^2+\sin^2 y}=r\sqrt{2(1-\cos y)} = 22$
portons tout au carré:

$r^2 (1+\cos x)=8$

$r^2 (1-\cos(x-y))= 98$

$r^2 (1-\cos y)=242$
Ou en notant

$X=\cos x$ et

$Y=\cos y$ , il vient :

$r^2 (1+X)=8$

$r^2 (1-XY-\sqrt{1-X^2}\sqrt{1-Y^2})= 98$

$r^2 (1-Y)=242$
Un ordi doit pouvoir résoudre ca mais j'ai la flemme.

scrablor · #3

Donc ce serait 14 cm...
Il va falloir que je comprenne

PS : J'aurais pu mettre l'inconnue au dénominateur, c'eût été plus logique et plus direct

dylasse · #4

r vérifie arcsin(11/r)+arcsin(7/r)+arcsin(2/r) = pi/2

solution r = 14 (solveur excell...)

Il doit y avoir une démo plus classe...

Vasimolo · #5

C'est plutôt bien parti , mais y'aura-t-il quelqu'un pour résoudre l'énigme sans solveur ou autre abominable machinerie

Vasimolo

MthS-MlndN · #6

14 cm.

Et je ne sais pas du tout pourquoi

Nicouj · #7

On peut diviser notre gâteau en 6 triangles isocèles dont les cotés égaux sont le rayon et le dernier coté un des cotés du gâteau (4, 14 ou 22).
Nous obtenons ainsi 2 exemplaires de trois triangles différents.

Les aires de ces triangles en fonction du rayon sont $4sqrt(r^2-4)$ , $7sqrt(r^2-49)$ et $11sqrt(r^2-121)$ .

Si on répartit différemment les six triangles on peut découper le gâteau en deux parts égales séparées par un diamètre et dont les 4 cotés sont 4, 14, 22 et 2r.
Ces parts sont des quadrilatères inscrits dans un cercle on peut donc exprimer leur aire en fonction de leur cotés : $sqrt{(r+16)(r+6)(r-2)(-r+20)}$

en comparant la somme des aires des trois triangles différents avec celle d'une moitié de gâteau, http://www.wolframalpha.com/ me répond 14 en approximation.
En remplaçant je trouve bien que 14 est correct.

scrablor · #8

Je sais démontrer que R=14 convient mais je ne vois pas comment aboutir à cette valeur...

Pour cette vérification, je note 2a l'angle qui intercepte les 22 cm et 2b celui qui intercepte les 4 cm. En traçant les bissectrices, j'obtiens deux valeurs utiles :

$sin a = \frac{11}{14}[/latex] et [latex]sin b = \frac{2}{14}$
Par suite :

$cos a = \frac{\sqrt{75}}{14}[/latex] et [latex]cos b = \frac{\sqrt{192}}{14}$
Une petite formule :

$cos(a+b)=cos a cos b - sin a sin b = \frac12[/latex] d'où [latex]a+b=\frac\pi3$
2a+2b valent donc 120° et un triangle équilatéral de côté 14 a un angle au centre de 60°, le total donne bien 180° avec un triangle de chaque sorte, donc 360° pour le tout.

Avec l'indice Ptolémée :
J'ai réorganisé les cordes à ma guise...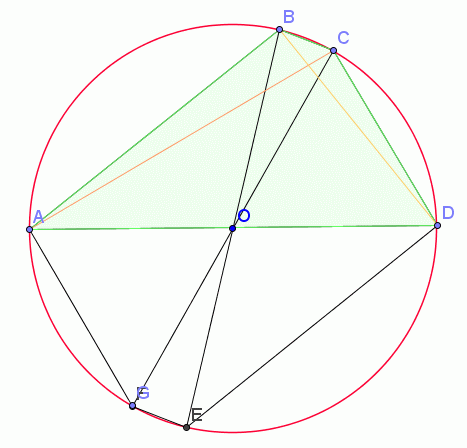

http://www.prise2tete.fr/upload/scrablor-gateau13.png

AB*CD+BC*AD=AC*BD
On connaît AB=22, BC=4 et CD=14.
On pose AD=2r et les longueurs AC et BD sont des troisièmes côtés de triangles rectangles.

En élevant au carré après division par 4 :

$(r^2-11^2)(r^2-7^2)=(2r+77)^2$

On réduit et ordonne :

$r^4-174r^2-308r=0$

On factorise :

$r(r-14)(r^2+14r+22)=0$

Il n'y a qu'une solution strictement positive : r=14.

J'avais tout oublié de Ptolémée.

Vasimolo · #9

Joli scrablor

Vasimolo

gabrielduflot · #10

methode intuitive
on dit que le périmètre du cercle est un peu plus grang que celui de l'hexagone donc en prenant pi=3 on aura une valeur approchée du périmètre de l'hexagone donc 6R=80 donc R=13.3

démonstration
si on trace les rayons sur le cercle de centre O on arrive à 6 triangles isocèles:
2 triangles isocèles de base 4 cm et d'angle à la base a°
2 triangles isocèles de base 14 cm et d'angle à la base b°
2 triangles isocèles de base 22 cm et d'angle à la base c°

la somme des angles d'un hexagone est de 720° donc 4(a+b+c)=720 donc a+b+c=180°

Si on prend un triangle de chaque et qu'on les colle les uns contre les autres alors l'angle en O est 180-2a+180-2b+180-2c=540-2(a+b+c)=540-360=180° donc il est plat

donc ce quadrilatère est inscrit dans un demi-cercle dont les côtés sont 4cm; 14cm; 22cm et 2R

puisque les point sont sur les demi cercle alors il y a 2 triangles rectangles donc les diagonales valent $\sqrt{4R^2-16}=2\sqrt{R^2-4}$ et $\sqrt{4R^2-196}=2\sqrt{R^2-49}$

donc d'après le théorème de Ptolémée

$4\sqrt{R^2-49}\sqrt{R^2-4}=4\times 14+22\times 2R$

$\sqrt{(R^2-49)(R^2-4)}=14+11R$

$R^4-53R^2+196=(14+11R)^2=196+308R+121R^2$

$R(R^3-174R-308)=0$
donc

$R=0 ou R^3-174R-308=0$

et en testant le rayon vaut 14 cm ou en faisant le méthode de Cardan que je n'ai jamais utilisé.....

looozer · #11

En permutant les deux cordes adjacentes de 14 et 22, j'obtiens un hexagone symétrique par rapport au diamètre du cercle.

Cet hexagone est formé de deux quadrilatères isométriques dont les côtés valent 4, 14, 22 et le diamètre (que je nomme 2a).

J'utilise le théorème de Ptolémée préconisé - merci pour l'indice

Si d1 et d2 sont les diagonales du quadrilatère, alors :
d1 x d2 = 22 x 4 + 14 x 2a

Les diagonales forment également deux triangles rectangles (car inscrits dans un demi-cercle). Par Pythagore on a :
(2a)² = 4² + d1²
(2a)² = 22² + d2²

Le système à 3 inconnue me donne par substitution a³ -174a - 308 = 0 qui a comme seule solution positive a = 14

C'est assez lourd et je sens que d'autres auront fait mieux

Vasimolo · #12

Bravo aussi à Gabriel et Looozer

Vasimolo

Vasimolo · #13

Que des bonnes réponses

Je préfère celles qui n'utilisent pas les solveurs ou autre ( ça n'engage que moi )

Ma solution est celle de scrablor et looozer , changer l'ordre des côtés , pythagore et Ptolémée . On tombe sur une équation de degré trois mais la solution "évidente" 14 apparait assez vite

Un grand merci pour la participation

Vasimolo

kosmogol · #14

MthS-MlndN a écrit:
14 cm.

ce n'est pas si mal, juste un peu en dessous de la moyenne

looozer · #15

Joli problème mariant agréablement logique, géométrie et algèbre

MthS-MlndN · #16

kosmogol a écrit:
MthS-MlndN a écrit:
14 cm.
ce n'est pas si mal, juste un peu en dessous de la moyenne

...au repos...

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 11-07-2010 00:44:53

Gâteua 13

#0 Pub

#2 - 11-07-2010 03:29:57

Gâtau 13

#3 - 11-07-2010 08:47:42

GGâteau 13

#4 - 11-07-2010 09:57:25

Gâtea 13

#5 - 11-07-2010 12:53:57

Gâteua 13

#6 - 11-07-2010 15:09:33

fâteau 13

#7 - 11-07-2010 15:51:54

Gâteau 113

#8 - 11-07-2010 20:12:12

Gâteau 1

#9 - 12-07-2010 13:16:36

Gâetau 13

#10 - 12-07-2010 14:12:00

Gâetau 13

#11 - 12-07-2010 22:04:25

Gâteau 3

#12 - 12-07-2010 22:57:40

Gâtau 13

#13 - 13-07-2010 23:57:47

Gâteau 1

#14 - 14-07-2010 00:39:54

Gâtteau 13

MthS-MlndN a écrit:

#15 - 14-07-2010 00:53:37

Gâteua 13

#16 - 14-07-2010 15:06:58

fâteau 13

kosmogol a écrit:

MthS-MlndN a écrit:

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums