255 heures pour une énigme aussi simple ?! Alors que Vasimolo laisse généreusement 96 heures pour les siennes ?! 
Si on suppose que la largeur est plus courte que la longueur, alors le plus grand rond que l'on pouvait découper dans le gâteau faisait 20 centimètres de diamètre, soit une aire de 100π. Bien sûr, ce rond a été découpé à mi-longueur pour qu'il suffise de trancher en deux dans le sens de la largeur pour avoir quatre parts identiques. L'aire totale du gâteau était donc de 200π d'où une longueur de 10π soit 31,415926... cm. La case réponse valide 314 mm.
Maintenant, si la largeur est plus grande que la longueur (ça dépend dans quel sens on pose le gâteau, non ?  )... Posons une longueur L. Vu qu'elle limite la taille du rond, le rond est de diamètre L, donc de rayon L/2, donc d'aire πL2/4. Cette aire vaut la moitié de l'aire totale du gâteau, qui est 20L. On veut donc résoudre πL2/4=10L. En virant la solution L=0, on obtient L=40/π soit 12,7 cm.
)... Posons une longueur L. Vu qu'elle limite la taille du rond, le rond est de diamètre L, donc de rayon L/2, donc d'aire πL2/4. Cette aire vaut la moitié de l'aire totale du gâteau, qui est 20L. On veut donc résoudre πL2/4=10L. En virant la solution L=0, on obtient L=40/π soit 12,7 cm.

 Accueil
Accueil
 Forum
Forum






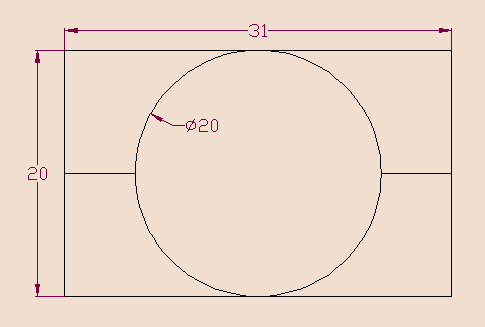
 (en millimètres)
(en millimètres)
