 |
#1 - 19-11-2011 19:16:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 19-11-2011 20:15:24
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
gâreau 45
C'est bien vague tout ça
La quatrième part est-elle triangulaire comme les trois autres?
Merci
#3 - 19-11-2011 23:03:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtzau 45
La 4ème part n'est volontairement pas décrite 
Vasimolo
#4 - 20-11-2011 11:03:26
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gââteau 45
La seule manière de découper trois triangles en 2 coups de couteau est de couper 2 fois en partant d'un sommet. La quatrième part n'est donc pas un triangle 
De là, le problème est assez trivial (euh, pas si trivial que ça vu que je me suis planté dans le premier jet  ) : ) :
Pour avoir un triangle, il faut que la plus grosse part soient placée entre les sommets d'où partent les traits de coupe.

La proportion de surface entre COH et COB étant de 1/3, O est au quart de [BH] et donc, H' est au quart de [AB]
De la même façon :
La proportion de surface entre BOH' et COB étant de 1/2, O est au tiers de [CH'] et donc, H est au tiers de [AC]
On peut alors symétriser le triangle vert OHH' dans OBC et en appliquant 2 fois la proportion des sécantes, on a :
aire(OHH')= aire(OBC) x 1/2 x1/3
aire(OHH') = 50
Edition:
Appelons a l'aire du triangle rouge
X le rapport AH/AC
Y le rapport AH'/AB
Dans le triangle ABC :
X(600+a) = 150+a
Y(600+a) = 200+a d'où XY= (150+a)(200+a) / (600+a)^2
Mais aussi : a = XY(600+a)
D'où, après simplification 30000 = 250 a
a=120
L'aire de la quatrième part est donc de 170
J'aime bien tes gâteaux, ils font un peu peur mais ils sont faisables sans trop de complication en fait.
Gwen.
#5 - 20-11-2011 19:16:32
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteu 45
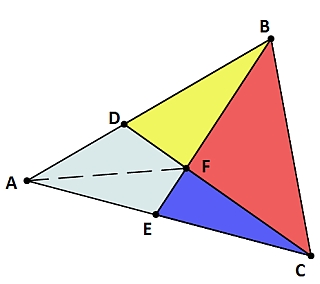
Je ne vois pas d'autre solution d'obtenir 4 parts, dont 3 triangles, en deux coupes rectilignes qu'en passant chaque fois par un sommet du gâteau triangulaire.
(*) Comme les triangles bleu et rouge une base appartenant à la même droite BE et même hauteur, le rapport de leurs aires 1/3 est égal au rapport EF/BF.
Par analogie, pour les triangles vert et rouge on a 1/2=DF/CF.
On trace AF qui permet de diviser les triangles AEB et ADC, chacun en deux parties triangulaires (AEF-AFB d'une part et ADF-AFC de l'autre) dont le rapport des aires vaut respectivement 1/3 et 1/2 pour les mêmes raisons qu'en (*)
Dès lors :
AEF / (AFD+150)=1/3 (j'attribue une aire égale à la masse en g)
AFD / (AFE+100)=1/2
En résolvant le système à deux inconnues, on obtient AEF=90 et AFD=80 dont la somme donne l'aire (et donc la masse) de la 4ème part : 170
#6 - 20-11-2011 20:53:01
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
Gâteaau 45
Juste pour être sûr :
Avant coupes, le gâteau du pâtissier est-il bien triangulaire...?
#7 - 20-11-2011 23:06:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
hâteau 45
Joli looozer 
Oui TiLapiot le gâteau est triangulaire !
Vasimolo
#8 - 21-11-2011 08:32:08
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
GGâteau 45
Même si je n'y arrive pas encore  , ma démarche est la suivante : , ma démarche est la suivante :
- je place le sommet B en (0;0)
- je choisis l’abscisse de C0 au hasard, par ex 50
- je choisis aussi l’ordonnée de M0 au hasard, par ex 20
- je n'impose pas encore de valeur à xM0, car elle est indépendante de la la surface de (BC0M0).
- je calcule la surface de (BC0M0), elle est de xC0.yM0/2, soit dans mon exemple de 50*20/2=500
- Comme il faut 300, c'est que mon triangle (BC0M0) est 5/3 trop grand, soit k ce coeff
- Je lui applique un coeff de sqrt(k), d'où sqrt(3/5) pour la base et la hauteur du gâteau rouge.
- j'obtiens xC=sqrt(3/5).xC0
- idem avec yM1=sqrt(3/5).yM0
- j'ai alors surface (BCM1)=300, qlq que soit xM1
- Comme le triangle jaune est 50% plus grand que le bleu, cela signifie que xM1/2−xB<xM1/2−xC, donc je fixe temporairement xM1 à 2/5 de xC
- je calcule les éq de droite de CM1 et de BM1
- pfff, que coquin de pâtissier, quand même 
- ensuite, je choisis A au hasard, soient xA et yA ses coord (avec 0<xA<xC et yM1<yA)
- j'en déduis les éq de droite de AB et AC, puis les coord de B' et C'
- par la formule de Héron, je calcule la surface de la part de gâteau bleu au cassis, et la part de gâteau jaune au citron
- comme A a été placé au hasard, et que xM1 est assez arbitraire, les surfaces des deux parts ne font ni 100 ni 150, mais je m'intéresse à leur ratio (=part jaune/part bleue)
- idéalement, ce ratio doit être de 150/100=3/2
- je glisse donc xM jusqu'à ce que le ration fasse exactement 3/2. Ouf, ça converge rapidement !
- ensuite il faut caler le point A. Le malheur, c'est qu'en le déplaçant, latéralement ou verticalement, ça modifie aussi bien la surface des deux petits triangles que leur.......
- ...
-> pour l'instant, je sèche pour obtenir une méthode optimale pour avoir les deux petites surfaces de 150 et 100 
#9 - 21-11-2011 11:06:23
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtea 45
170 g avec deux coupes
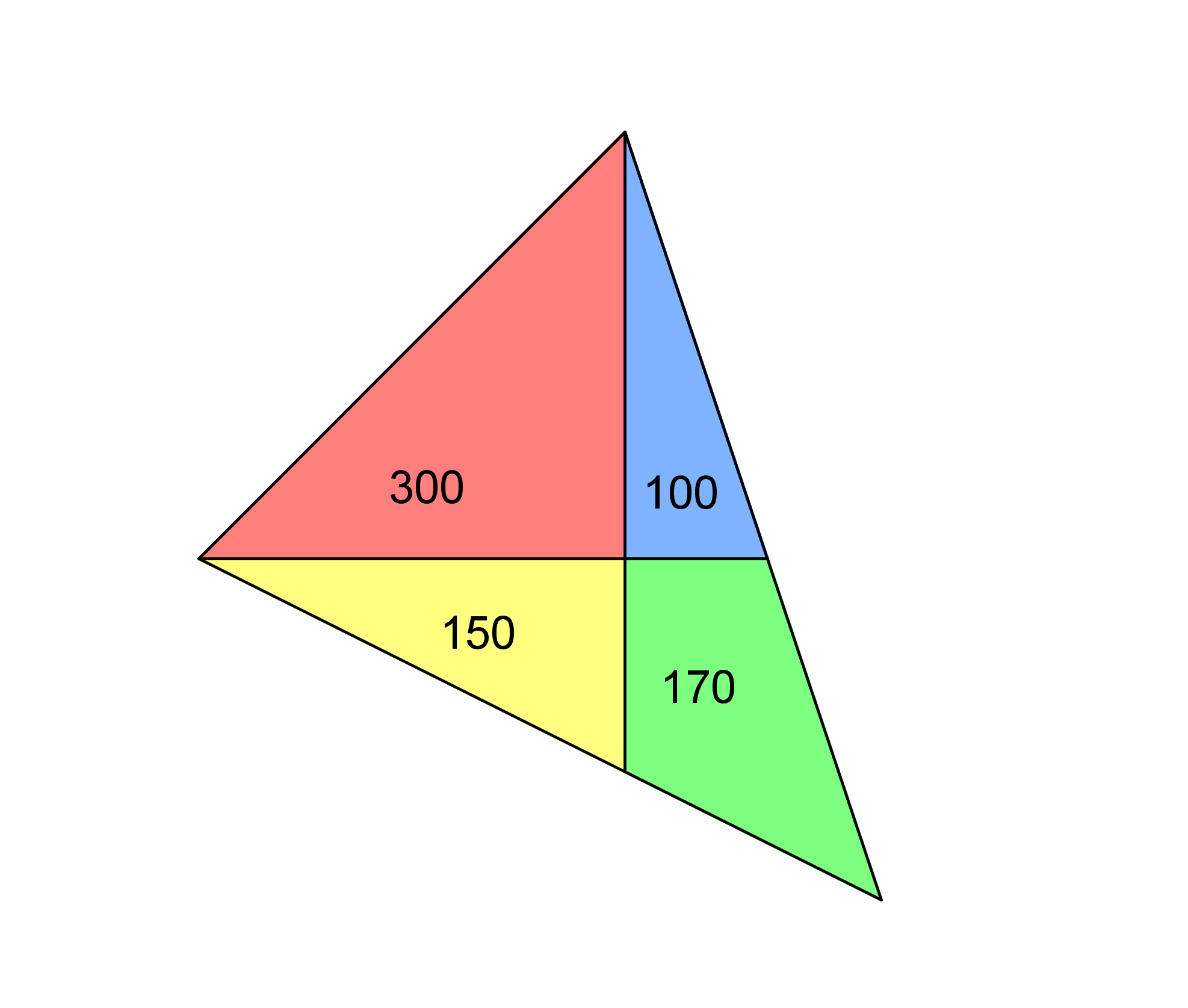
#10 - 21-11-2011 11:58:55
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Gâteau 4
Bonjour !
Est-ce que la découpe ressemblait à cela ?
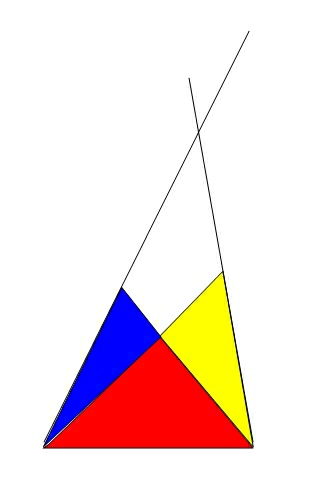
Sous quel format faut-il proposer une réponse, juste la valeur ? (ou bien " g") ?
Je continue de chercher l'aire de la quatrième part ...
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#11 - 21-11-2011 12:15:46
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâteau 455
peut-on avoir les dimensions des 3 triangles? ou les angles?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#12 - 21-11-2011 14:24:38
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
âteau 45
Ce midi, requinqué en carotène, j'ai une autre méthode de construction, sans Excel ni WinGeom :

- je place le sommet B en (0;0), et C n'importe où sur l'axe des abscisses positives
- cela détermine la base du triangle (ABC)
- pour être sûr d'avoir une surface rouge égale à 300, il suffit de choisir l’abscisse yM=600/xC
- comme le triangle jaune est 50% plus grand que le bleu, je fixe xM à 2/5.xC, quitte à déplacer plus tard son abscisse
- on a donc M connu en f° de xC, soit M(2/5.xC;600/xC)
- je calcule l'éq de la droite (BM) : elle passe par B(0;0) et M(2/5.xC,600/xC), d'où y=(1500/x²C)*x
- je calcule l'éq de la droite (CM) : elle passe par C(xC;0) et M(2/5.xC,600/xC), d'où y=1000(xC-x)/x²C
- on sait que la surface du triangle (BMC') vaut 100
- le point C' est le sommet du triangle bleu BMC', et C' est situé sur une parallèle à BM
- sa base est BM = sqrt(x²M+y²M) =sqrt((2/5.xC)²+(600/xC)²)
- pour obtenir une surface de 100, il faut que la hauteur de (BMC') soit égale à 200/BM
- le point C' est aussi sur la droite (CM) dont on connait déjà l'éq de droite
- on peut donc calculer les coord de C' en f° de xC, ainsi que l'éq de la droite BC'
- ............
- On procède de même avec B' (même problématique que C')
- le sommet A étant l'intersection des droites (BC') et (CB'), on détermine A
Spoiler : [Afficher le message] Bon, y avait une part de fraisier, une autre au citron, et la 3è au cassis, ..., mais elle était à quoi la %#£¤ part de gâteau du haut   
#13 - 21-11-2011 17:48:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteaau 45
Une réponse rapide avant de partir au bad :
@Gwen : c'est bon
@TiLapiot : cherche plus simple .
@Halloduda : le pâtissier n'a fait que deux coupes droites .
@NickoGecko : oui ( 100 pour 100 g dans la case réponse ) .
@Dan : tu dois pouvoir te débrouiller avec les indications fournies .
Bonne continuation 
Vasimolo
PS : si vous voulez un peu de rab de temps , il suffit de demander .
#14 - 21-11-2011 18:09:41
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
#15 - 22-11-2011 01:02:38
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
GGâteau 45
Vasimolo a écrit:@Dan : tu dois pouvoir te débrouiller avec les indications fournies .
Comme les formes donnees ne sont pas proportionnelles aux surfaces donnees, je ne sais pas si les dimensions des figures sont mauvaises ou les angles sont mauvais... Si on commence a modifier les angles, je suppose qu'il y a plein de solutions....
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#16 - 22-11-2011 11:41:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteaau 45
@Dan : il y a plusieurs formes possibles pour les trois premières parts et donc pour la 4ème mais la masse de celle-ci est bien déterminée .
Vasimolo
#17 - 22-11-2011 23:11:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtau 45
Une petite relance pour ceux qui ont trouvé 
Initialement ( certains l'ont peut-être vu ) j'avais proposé des parts de 100g , 275g et 300g mais j'ai choisi de changer ces valeurs .
Ce n'est pas pour que la réponse soit plus aisée ou pour que le résultat soit entier alors pourquoi ?
Vasimolo
#18 - 23-11-2011 11:31:52
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâtzau 45
Parce que dans le cas des nouvelles valeurs, il n'y a qu'une possibilité pour placer les triangles. Si les traits de coupe partent des sommets d'une autre forme , les deux autres côtés "s'écartent"... la forme du gâteau n'est donc plus triangulaire.
Démonstration avec 150 central (c'est encore pire avec 100)

Tandis qu'avec les premières mesures, 2 cas sont possibles : 275 ou 300 en position "centrale" avec des résultats différents.

#19 - 23-11-2011 15:22:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#20 - 25-11-2011 00:09:19
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
gâtrau 45
Très belle énigme ; merci Vasimolo 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum













