Bonjour, 
découpons le gâteau en 9 carrés.
Si l'une des coupes passe strictement par 5 carrés, alors le seul moyen pour que les 2 coupes passent par les 9 carrés est de faire la coupe de 5 en "escalier" et la coupe de 4 passant par les 4 derniers carrés.
On remarque alors que les deux coupes passent par le carré central. En plaçant un coin du carré au point d'intersection des coupes, et en orientant le carré dans une direction ou l'angle formé par les coupes est obtus, on case le carré à l'aise.

Bonjour le Pâtissier.

Je n'ai pas trouvé de cas où c'est impossible.

il faut distinguer 2 cas. Soit les coupes se croisent ou non et chercher le cas pire où les 3 ou 4 morceaux sont identiques.

3 morceaux rectangulaires de 15x5 ou 4 triangulaires obtenus par 2 coupes diagonales.

dans ces 2 cas le carré touchera les bords.

Ce raisonnement est dicté par mon intuition je ne saurais faire une démonstration.

Cordialement

On ne peut pas couper les 9 carrés élémentaires 5*5 qui composent le carré 15*15.

Oui, en effet, on peut.
Mais du coup, cette config est très restrictive pour le placement des 2 lignes (intersection dans le carré du milieu, orientation entre tg 1 et tg 3) et résout pratiquement le problème.

Salut Vasimolo,

j'ai une idée pour démontrer qu'il peut le faire, mais il y a peut être plus simple.

On commence par quadriller le gâteau en 3x3 carrés de 5 cm de côté. On s'intéresse ensuite aux carrés à l'intérieur desquels les deux coupes vont passer : si l'un des 9 carrés est épargné, il suffit d'y placer la feuille de menthe, et le problème est résolu.

Or, il n'existe qu'une façon de n'épargner aucun des 9 carrés, c'est quand chacune des coupes recouvre 5 carrés formant un pentamino "Z" (les deux pentaminos s'obtenant l'un à partir de l'autre par une rotation de 90°).

Les deux coupes s'intersectent alors dans le carré central. Autour du point d'intersection I, les deux coupes forment deux angles obtus opposés. On trace la bissectrice de ces deux angles, elle coupe le bord du gâteau en A et B. Comme AB >= 3 > 2*racine(2), on en déduit que IA ou IB > racine(2). Mettons que ce soit IA, on peut alors placer la feuille de menthe avec un sommet en I, et une diagonale dans la direction de IA.

Bonjour ,

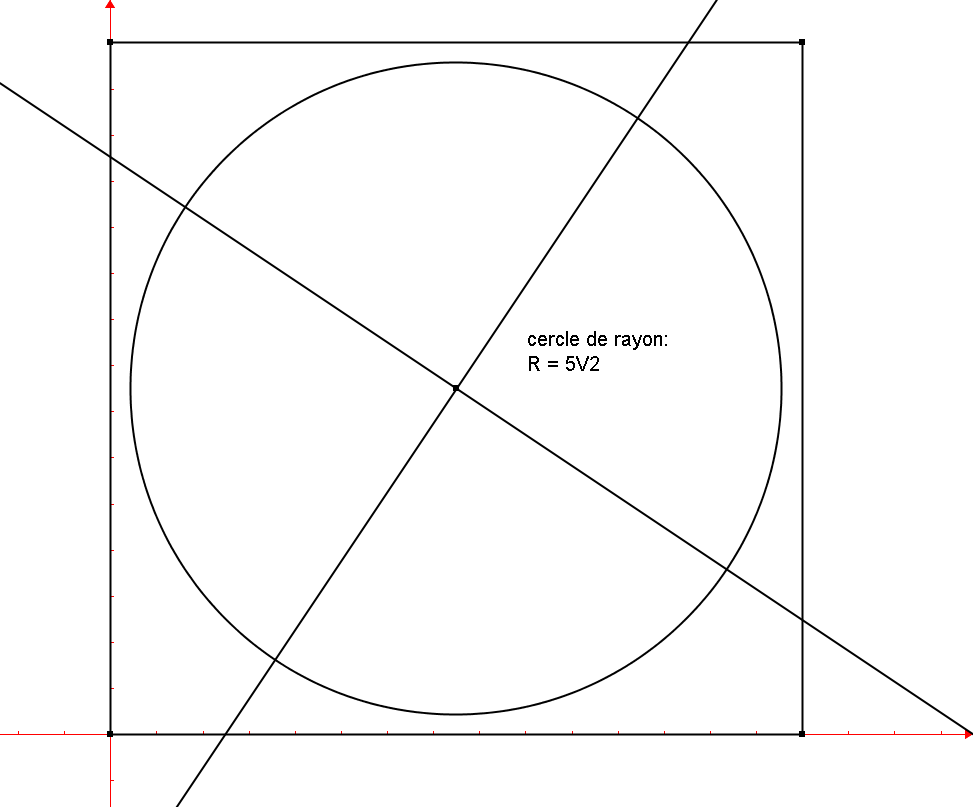
Je dirais que dans le pire des cas le gateau est partagé en 4 parts égales d'aire : 56.25
La feuille de menthe d'aire : 25 tient dans un des 4 quarts de cercle de rayon 5V2 .
et d'aire 39.27

Faisons simple, mais détaillé :

1 ) Une droite ne peut traverser que deux carrés en coin au plus, deux carrés sur le côté au plus et le carré central, soit 5 des 9 carrés de 5x5.

Une des deux droites doit donc en couper 5 strictement, et l'autre, au moins 4.
Cela ne peut se faire que de deux façons.
La première solution est impossible, car la seconde droite ne peut pas couper les 4 autres carrés. L'un d'entre eux resterait libre pour lui superposer la feuille de menthe.

On est donc, après un peu trop de blabla pour une évidence, dans le second cas de figure :


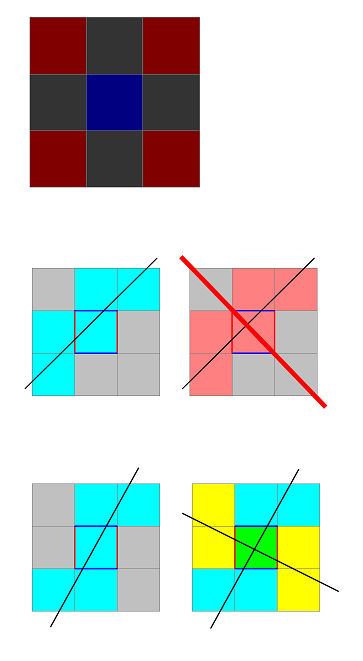
2 ) Une droite coupe donc strictement deux côtés opposés du carré central et l'autre coupe les deux autres. On peut prolonger ces segments jusqu'au carré suivant.


3 ) Si un trait vert est plus grand que 5, il permet de caser la feuille de menthe au bord.  Chacun des traits verts est donc plus petit que le côté du carré central.


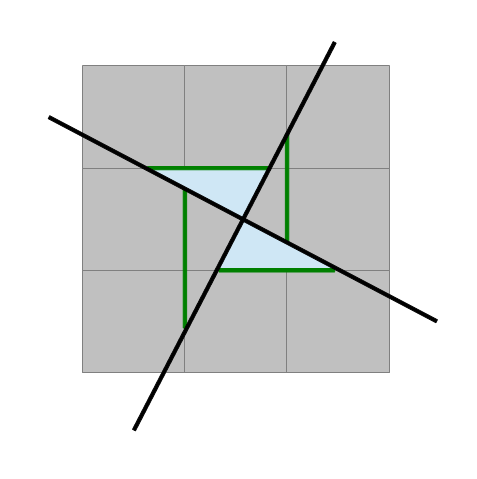
L'aire en bleu clair est donc plus petite que la demi-somme des côtés par la hauteur, soit 25/2. Pareil pour son pendant.
L'espèce d'hélice, qui englobe le carré central strictement serait plus petite que le carré central, ce qui est impossible. Un des traits verts est donc plus grand que 5, on peut loger la feuille de menthe.