|
#1 - 03-10-2017 22:48:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#2 - 04-10-2017 13:32:01
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,096E+3
Gâteua 145
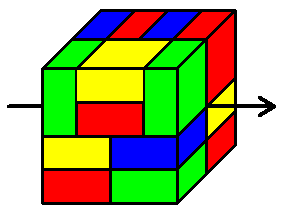
Impossible, ils vont par paire (de même position et de même orientation selon leur axe central).
Or, il en faut 3 x 19 x 19 dans des positions qui s'excluent.
Il en faudrait donc 1083 x 2 , on n'en a que 2000.
#3 - 04-10-2017 16:09:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 154
C'est ça Gwen , comment justifies-tu cet appariement ?
Vasimolo
#4 - 04-10-2017 16:43:32
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,096E+3
hâteau 145
Juste par parité le long d'une arête, les deux autres sortes de forme amenant une dimension 2.
Puis par récurrence, une fois les "bords" du cube remplis avec cette contrainte.
#5 - 04-10-2017 18:45:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtteau 145
Pour les arêtes c'est clair mais je ne vois pas comment tu étends ça à l'ensemble du cube , la récurrence fonctionne assez mal avec un cube quelque peu boutonneux .
Vasimolo
#6 - 04-10-2017 19:12:01
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,096E+3
Gâteau 415
Si je remplis uniquement une couche d'une face du cube, sur une épaisseur (dépassant ou pas sur la seconde couche ) les éléments "dépassant" seront en nombre pair dans les deux dimensions quelles que soient la ligne ou la colonne (sinon, la première couche n'est pas remplie) . Ils le seront donc sur la couche suivante que je dois finir de remplir avec le même constat, partant d'un nombre pair pour arriver à un nombre pair.
#7 - 04-10-2017 19:51:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteai 145
D'accord , la récurrence démarre après le remplissage d'une face 
On peut faire plus simple avec une petite astuce .
Vasimolo
#8 - 05-10-2017 12:11:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteai 145
J'ai ajouté un indice dans le message initial .
Il ne faut surtout pas chercher quelque chose de compliqué 
Vasimolo
#9 - 05-10-2017 19:56:05
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gââteau 145
Il y a 19*19*3=1083 axes. Il y a 2000 caramels, et chaque caramel ne bloque qu'un axe ; or comme les caramels sur un même axe sont en nombre pair, il y a au plus 1000 axes recouverts, et donc on peut traverser le grand cube de 83 façons différentes au moins.
La difficulté est de prouver que les caramels sur un même axe sont en nombre pair. Or je vois ça par récurrence, comme gwen27 si je comprends bien.
Découpons notre grand cube en minces colonnes verticales de 1x1x20, et prenons une de ces colonnes. Chaque caramel vertical (deux directions différentes) qui recouvre cette colonne en recouvre 2 cubes unité 1x1x1. Donc il y a un nombre pair de caramels horizontaux qui recouvrent cette colonne, chacun recouvrant un unique cube unité. Le problème est que ces caramels horizontaux ne sont a priori pas appariés en caramels de même axe ; or c'est bien le cas.
Pour le prouver, on considère une colonne verticale placée dans un coin du cube ; les caramels horizontaux qui la recouvrent sont tous alignés sur un même axe, les caramels sur cet axe sont donc en nombre pair. Si je considère une colonne juste à côté, les caramels horizontaux qui la recouvrent sont les mêmes caramels que ci-dessus (donc en nombre pair), ou ceux alignés sur un axe adjacent, qui sont donc aussi en nombre pair. De proche en proche, on montre cette propriété pour chaque axe vertical.
Il suffit enfin de faire pareil pour les deux autres directions.
#10 - 05-10-2017 22:26:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtea u145
Oui Ebichu , tu as la même approche que Gwen 
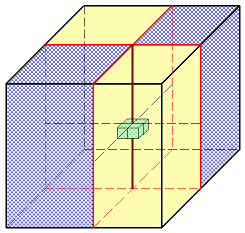
As-tu regardé ce qui se passait si le caramel vert était le seul sur son axe ?
Vasimolo
#11 - 06-10-2017 08:01:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteaau 145
Ha oui, je n'avais pas vu l'indice.
Effectivement, le caramel vert serait le seul à contribuer pour 1 cube unité dans la colonne jaune de devant, les autres caramels contribuant pour 2. Ce qui contredit que le nombre de cubes unité dans la colonne jaune soit pair. Joli 
#12 - 06-10-2017 12:44:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gââteau 145
Voilà Ebichu , ces problèmes de parité sont toujours très bluffant 
Vasimolo
#13 - 07-10-2017 09:53:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
|
 |

 Accueil
Accueil
 Forum
Forum