|
#1 - 23-11-2014 19:35:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 25-11-2014 19:31:03
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteauu 84
J'ai cherché, mais sans rien trouver !
Tout ce que je peux dire, c'est que même couper un pentagone en 4 morceaux identiques semble impossible...
#3 - 25-11-2014 22:46:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gtâeau 84
On est sur la même voie et rassures-toi , je ne suis pas beaucoup plus loin que toi 
Vasimolo
#4 - 25-11-2014 23:48:17
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
gâtzau 84
Tous !
Sauf si tu veux que les parts respectent des règles supplémentaires (découpes droites, extrémités sur la circonférence ou au centre, symétries...). 
Non ?
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#5 - 26-11-2014 18:08:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
GGâteau 84
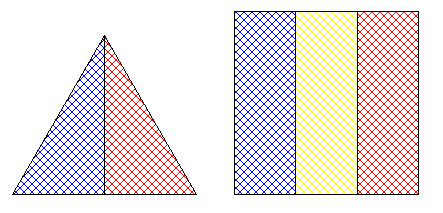
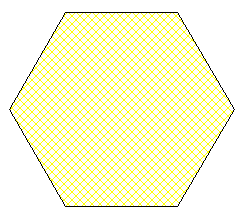
Tu peux donner un exemple pour l'hexagone par exemple 
Vasimolo
#6 - 27-11-2014 09:31:05
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Gâteau 8
Je crois que fix33 a fait la même erreur que moi à ma première lecture : découper un pentagone régulier à n cotés en n parts égales.
Là, ça semble évident.
Mais pour n-1 parts, je pense qu'il n'y a pas d'autres exemples.
#7 - 27-11-2014 21:08:02
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
gâreau 84
Quand on veut on peut dit l'adage, je pense qu'on peux pour tous, mais tout dépend de ce que tu appelles un part, du moins d'un point de vue géométrique, la part doit-elle être constructible au "compas et a la règle" ? Si non, alors on peut tout se permettre, surtout en considérant que la matière est strictement homogène. 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#8 - 27-11-2014 23:59:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteauu 84
Si on doit toujours tout dire ...
Le problème laisse entendre que les parts sont des polygones superposables 
J'ai plein d'idées qui me laissent penser que le problème peut se résoudre simplement mais j'ai peu de temps libres en ce moment . J'aime bien aussi qu'on me propose des idées , je vais donc attendre encore un petit peu avant de donner les miennes 
Bien sûr si je trouve je donne des indices , à bientôt .
Vasimolo
#9 - 28-11-2014 23:05:24
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâteaau 84
C'est super intéressant, je me penche dessus
Un promath- actif dans un forum actif
#10 - 29-11-2014 13:51:10
- 7nyguita7
- Professionnel de Prise2Tete
- Enigmes résolues : 43
- Messages : 155
- Lieu: Lognes
Gâteau 48
Je pense que c'est impossible pour les polygones à 4x+1 cotés (pentagone, nonécagone...). En effet, voilà pourquoi:
Si un polygone peut-être divisé en 4 parties égales, on peut regrouper deux à deux les parts pour obtenir deux parts identiques...Donc pour couper une figure en 4, il faut d'abord couper en 2, puis couper part en 2 parts identiques, or
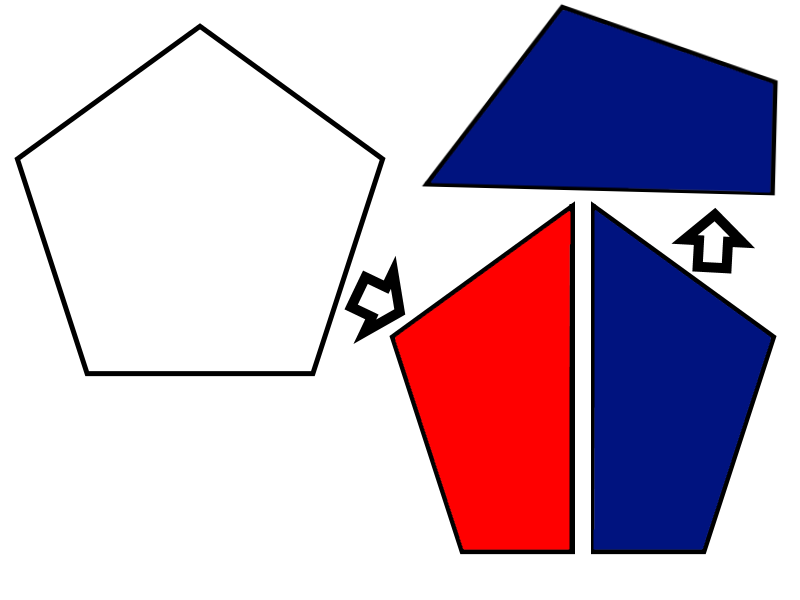
Le morceau bleu ne peut ne se diviser en 2 et donc le pentagone ne peut pas diviser en 4.
Même chose chose pour le nonécagone.
Je ne sais pas si cela s'applique aux autres polygones avec des nombres de cotés impaires...Mais ça nous arrangerait beaucoup
Même une feuille de papier est plus légère à deux (Proverbe coréen)
#11 - 29-11-2014 14:18:35
- Puuma
- Habitué de Prise2Tete
- Enigmes résolues : 49
- Messages : 11
Gâtau 84
Dans l'épaisseur !!
(héhé)
#12 - 29-11-2014 15:48:21
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
gâteay 84
N°7, pourquoi le morceau bleu ne peut pas être coupé en 2 ?
D'un coup de ciseau, je suis d'accord, mais avec une découpe plus complexe...
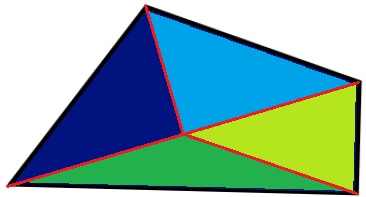
En la découpant comme ci-dessous, les deux triangles verts on la même aire (triangle rectangle coupé en deux par le milieu de l'hypoténuse), et les deux triangles bleus aussi (triangle isocèle coupé en deux par le milieu de la base). Du coup, le quadrilatère formé des 2 triangles clairs a la même aire que le quadrilatère formé des 2 triangles foncés.
Je sais bien que ces 2 quadrilatères sont différents, mais qu'est-ce qui dit qu'en modifiant les découpes, on ne peut pas y arriver...
#13 - 29-11-2014 16:09:44
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâeau 84
Puuma a écrit:Dans l'épaisseur !!
(héhé)
J'ai déjà essayé, on me l'a refusé, les gâteaux de Vasimolo sont des gâteaux mathématiques ils n'ont donc pas d'épaisseur... 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#14 - 29-11-2014 16:23:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 844
shadock a écrit:J'ai déjà essayé, on me l'a refusé, les gâteaux de Vasimolo sont des gâteaux mathématiques ils n'ont donc pas d'épaisseur... smile
Et pourtant ils ne sont pas toujours très fins 
Vasimolo
#15 - 29-11-2014 16:49:32
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
hâteau 84
Bonjour,
Peut-être y-a-t-il un lien avec le fait que le triangle équilatéral et le carré sont les seuls polygones réguliers qui peuvent être pavé "par eux-même en miniature". C'est à dire que le triangle équilatéral peut-être pavé par des triangles équilatéraux plus petits, et le carré peut être pavé par des carrés plus petits.
Mais je ne vois pas comment exploiter cela. 
Il y a sûrement plus simple.
#16 - 29-11-2014 17:36:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteu 84
J'y avais pensé Cogito ou plutôt : on y avait pensé pour moi 
Le problème restant sans réponse comme les gâteaux 82 et 78 , je les ai proposés à d'autres sites qui sèchent autant que nous pour le moment .
Vasimolo
#17 - 29-11-2014 19:19:56
- Lui-meme
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2762
- Lieu: Île de France
Gâteau 48
Bon, rien de génial mais après tout ça s'appelle un parallélogramme, ce n'est pas un carré et c'est un polygone régulier... 

#18 - 29-11-2014 19:23:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 84
Je ne crois pas que le parallélogramme entre dans la catégorie des polygones réguliers 
Vasimolo
#19 - 29-11-2014 20:08:51
- Lui-meme
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2762
- Lieu: Île de France
Gâteau 884
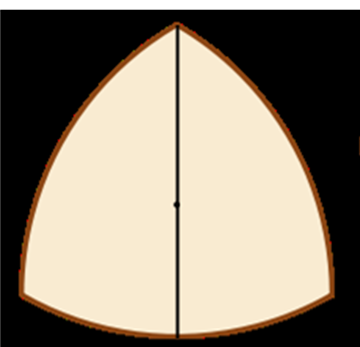
Et un triangle de Reuleaux, c'est valable...? 
#20 - 29-11-2014 21:08:35
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Gâteu 84
Oui mais non parce qu'un polygone est une ligne fermée formée de segments de droite et pas d'arcs ...
#21 - 29-11-2014 23:37:50
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
gâtzau 84
Ça dépend de la géométrie, par exemple la géométrie de l'espace temps est telle que la terre ce déplace en ligne droite et non pas en tournant autour du soleil comme le veux la tradition newtonienne 
Donc les arcs dépendent du référentiel 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#22 - 30-11-2014 10:57:37
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Gâteu 84
Ah oui la géométrie de l'espace-temps ... Je ne pense pas que le pâtissier de Vasimolo travaille dans un référentiel espace-temps, hein. 
Mais les polygones réguliers ne sont-ils pas définis uniquement en géométrie euclidienne ?
#23 - 30-11-2014 14:55:04
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâteau 48
Nous vivons dans l'espace-temps mon cher Saban ! 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#24 - 30-11-2014 15:33:19
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
GGâteau 84
Oui je sais mais imaginons je suis un pâtissier, je vais pas faire un gâteau en forme de triangle de Reuleaux et rétorquer à mon client qui veut un gâteau en forme de triangle : "Nous vivons dans l'espace temps ! Donc c'est bon !".
Puis je pense que Vasimolo avait en tête lorsqu'il a proposé l'énigme aux polygones réguliers "habituels" dans le référentiels espace en deux dimensions.
Après on peut élargir le problème mais on n'a pas encore trouvé de preuve pour la possibilité de découper ou non dans le problème initial.
Pour revenir au problème initial.
cogito a écrit:Bonjour,
Peut-être y-a-t-il un lien avec le fait que le triangle équilatéral et le carré sont les seuls polygones réguliers qui peuvent être pavé "par eux-même en miniature". C'est à dire que le triangle équilatéral peut-être pavé par des triangles équilatéraux plus petits, et le carré peut être pavé par des carrés plus petits.
Mais je ne vois pas comment exploiter cela. 
Les hexagones aussi peuvent être pavés par des hexagones plus petits, non ,
#25 - 30-11-2014 16:14:10
- Lui-meme
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2762
- Lieu: Île de France
Gtâeau 84
Saban pâtissier!  a écrit: a écrit:Oui je sais mais imaginons je suis un pâtissier, je vais pas faire un gâteau en forme de triangle de Reuleaux et rétorquer à mon client qui veut un gâteau en forme de triangle.
Et si je t'offre ce moule, tu ne me ferais pas qques petites bouchées Reuleaux de chocolat...? 

Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum