 |
#1 - 29-05-2011 19:38:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#2 - 29-05-2011 20:39:01
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteau 3
10\sqr2≈14.14
On trouve facilement le centre -10, -2.
Et la puissance de la cerise par rapport au Saint-Pierre
=d²-R²=-8x12=-24x4=10²+2²-R²
d'où R²=96+4+100=200.
#3 - 29-05-2011 20:50:26
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
Gâteu 39
2r =abc / 2s
r = abc / 4s
s=24*20/2 = 24 * 10 = 240
a=rac(8^2+24^2) = rac (640)
b=rac(24^2+12^2)= rac(720)
c= 8+12 = 20
r= rac (184320000) / 960
r =rac(200) = 10 rac(2)
Au pif, je me lance ....
#4 - 29-05-2011 22:15:16
- Kikuchi
- Passionné de Prise2Tete
- Enigmes résolues : 46
- Messages : 91
Gâtea 39
Si l'on choisit la cerise comme centre d'un repère orthonormé, alors trois points appartenant au cercle sont: (0;8) , (0;−12) et (−24;0)
Ces trois points satisfont alors l'équation (x−a)2+(y−b)2=R2 avec bien sûr (a,b) les coordonnées du centre dans ce repère et R le rayon.
Pas besoin de calcul pour voir que b=−2 car la cerise est à 2 du milieu de l'arc la corde vertical.
Les points (0;8) et (−24;0) nous donnent le système: \left\{ \begin{tabular}{r c l} a^2+(8-b)^2 &=& R^2\\ (-24-a)^2+b^2 &=& R^2 \end{tabular} \right. \Rightarrow \left\{ \begin{tabular}{r c l} a^2+100 &=& R^2\\ a^2+48a+24^2+4 &=& R^2 \end{tabular}
Qui une fois résolu nous donne a=−10 et R=10√2
EDIT: La corde et non l'arc vertical.
There's no scientific consensus that life is important
#5 - 29-05-2011 22:55:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtaeu 39
Déjà trois bonnes réponses et trois méthodes différentes 
Vasimolo
#6 - 30-05-2011 00:19:53
- socato314
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
#7 - 30-05-2011 10:54:25
- Autleaf
- Passionné de Prise2Tete
- Enigmes résolues : 48
- Messages : 71
- Lieu: Toulouse
gâteai 39
On peut exprimer simplement le diamètre d'un cercle circonscrit à un triangle grâce à la formule :
D = abc/(2S)
a = 20, et on utilise Pythagore pour b et c :
b = racine (24²+12²) = 26.8328...
c = racine (24²+8²) = 25.2982...
S = 20*24/2 = 240
D'où le diamètre :
D = 28.2842712...
Cohérent par rapport à la valeur attendue en voyant le dessin 
#8 - 30-05-2011 11:40:51
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
gâteay 39
On a:
abc/2S=2R
a=20
b=12rac(5)
c=8rac(5)rac(2)
On obtient b et c par Pythagore
Donc R=(20*12rac(5)*8rac(5)rac(2))/(20*24*4)
après simplification:
R=10rac(2)
#9 - 30-05-2011 11:42:10
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
gâyeau 39
Enfin un gâteau que je peux croquer...
Je considère le triangle formé par les 3 points d'intersection entre le cercle et les segments pointillés.
Les longueurs des côtés sont: 20;8.√10(=√82+242);12.√5(=√122+242).
On cherche le rayon du cercle circonscrit à ce triangle, qui est donné par la formule (à connaître absolument):
R=abc4S
Reste à connaître S.
Le triangle étant rectangle "en la cerise", sa hauteur vaut 24 et sa base 20, donc sa surface: 20*24/2.
Finalement R=20×8√10×12√54×12×20=10√2.
Pas la peine de préciser la dédicace 
Merci pour cette énigme.
#10 - 30-05-2011 12:00:53
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
Gâtea u39
1ère méthode:
En partant de l'équation du cercle:
(a-x)²+(b-y)²=r²
J'ai le système de 3 équations à 3 inconnues suivants en prenant la cerise comme origine (0,0):
a²+(b-8)²=r²
a²+(b+12)²=r²
(a+24)²+b²=r²
En soustrayant les deux premières, on trouve b=-2.
En soustrayant les deux dernières, on trouve a=-10.
D'où r=10V2.
2ème méthode:
En utilisant la peu connue formule du rayon:
r = (a+b+c) V(-c/a)
avec a=24, b=8 et c=-12
r= 10V2
#11 - 30-05-2011 12:09:03
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
Gâtau 39
Bonjour,
Soit la cerise l'origine du repère orthonormé.
Soient le point M(x;y) le centre du cercle et R son rayon.
Par symétrie, on voit que l'ordonnée y vaut -2.
L'abscisse x est telle que (-x)² + 100 = R² soit x = V(R²-100).
On écrit que le point à gauche appartient au cercle:
(24 - V(R²-100))² + 4 = R² et on trouve R = 10V2 = 14,142 env.
Bonne journée.
Frank
#12 - 30-05-2011 12:53:34
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâtau 39
En posant les équations, je trouve R=sqrt200=10∗sqrt2=14.14213562...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#13 - 30-05-2011 13:36:01
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Gâtea u39
Le diametre du cercle circonscrit est
D=abc/2A=2R
avec A=bh/2 on obtient
R=√(242+82)(242+122)48=10√2
Edit:
On note que le centre du gâteau est le centre du carré inscrit de côté 20 ce qui indique que d'autres méthodes de résolution plus astucieuses sont probablement envisageables.
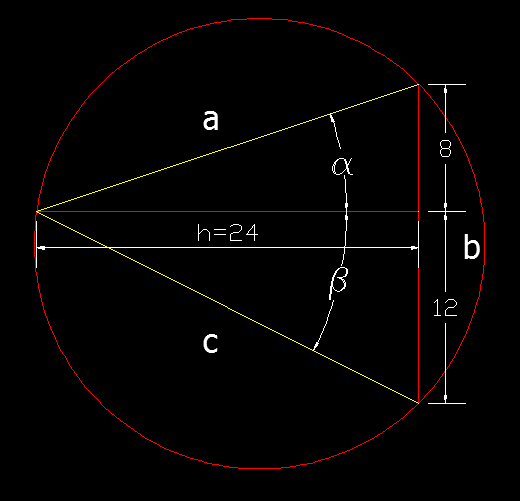
on cherche à calculer l'angle α+β
tan(α+β)=tan(a)+tan(b)1−tan(a)tan(b)tan(α+β)=8+12241−8∗12242=1
donc α+β=45 deg ce qui implique que b=20 est le côté du carré inscrit
The proof of the pudding is in the eating.
#14 - 30-05-2011 14:28:19
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Gâteaau 39
Soient A, B et C les extrémités des segments de longueurs respectives 24, 12 et 8, D le point de la cerise et O le centre du cercle.
L'angle BAD vaut arctg (1/2), l'angle DAC vaut arctg (1/3).
La somme de ces 2 arcs vaut, comme par hasard, 45°.
L'angle BAC vaut donc 90°.
Le triangle OBC, à la fois isocèle et rectangle a une hypoténuse = 20, le rayon du SaintPierre vaut donc 10∗√2, soit environ 14.14 (cm ??)
#15 - 30-05-2011 23:12:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâetau 39
Encore plein de bonnes réponses avec des méthodes toujours originales 
La réponse que j'attends ( ou plutôt son auteur ) n'est toujours pas au rendez-vous , patience ...
Vasimolo
#16 - 31-05-2011 09:39:47
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Gâteeau 39
Je note A la cerise et B,C,D les autres points numérotés dans le sens trigonométrique .
On a DB/sin(^DCB)=2R où R est le rayon cherché.
sin(^ACB)=8/√242−82cos(^ACB)=24/√242−82sin(^ACD)=12/√242−122cos(^ACD)=24/√242−122
R=10.192√6/24∗20=4√6.
J'ai juste un doute sur les formules de trigonométrie et les angles géométriques.
Un mathématicien complet est topologiquement fermé!
#17 - 31-05-2011 22:07:05
- catduc
- Amateur de Prise2Tete
- Enigmes résolues : 18
- Messages : 1
#18 - 31-05-2011 22:29:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
gâteai 39
Au moins , il y a des réponses ...
On cherche quoi ? A première vue , il existe une solution en quelques mots qu'on loupe. Un indice ?
#19 - 31-05-2011 22:54:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 3
Les trois dernières réponses sont incorrectes 
Je ne donnerai pas d'indice car il y a de très nombreuses approches possibles dont certaines très simples ( avec quelques souvenirs de géométrie de lycée ) .
Vasimolo
#20 - 01-06-2011 07:39:39
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
gâyeau 39
Vasimolo dit moi juste si la faute est dans le raisonnement.
J'utilise la formule d'addition à la fin, ais-je le droit?
J'avais une petite faute de calcul.
Merci.
Un mathématicien complet est topologiquement fermé!
#21 - 01-06-2011 09:29:35
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
âteau 39
Avec les mêmes idées au départ mais en utilisant Al-Kashi j'arrive à
10√2.
Je détailerai si c'est juste et si personne n'a fait comme cela.
Au fait, je suis une bille en géometrie.
Un mathématicien complet est topologiquement fermé!
#22 - 01-06-2011 20:21:25
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Gâtea 39
Je prendrais les notations de la figure de Franck9525.
On a b²=a²+b²-2abcos(b) d'où après quelques calculs en utilisant pythagore cos²(b)=1/2. On a donc sin²(b)=1/2 , or b/sin(b)=2R car c'est le cercle circonscrit...
Je n'ai pas détaillé, c'est juste pour montrer l'idée.
Un mathématicien complet est topologiquement fermé!
#23 - 02-06-2011 00:42:55
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâteu 39
J'ai honte de ne pas avoir réussit à utiliser l'équation du cercle correctement alors que c'est le dernier chapitre que j'ai fait ! 
Heureusement j'ai compris toutes le réponses 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#24 - 02-06-2011 10:21:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtea 39
Merci pour toutes ces réponses 
J'avais procédé à peu près comme halloduda . La puissance de la cerise par rapport au cercle vaut 8X12=24X4 , on connait donc la taille des deux cordes . On trace les médiatrices ( en rouge sur le dessin ) et Pythagore donne immédiatement le rayon du Saint-Pierre .

C'est toujours intéressant de voir le nombre incroyable d'approches possible pour un simple petit exercice , c'est ce qui fait le charme de la géométrie .
Vasimolo
Edit : pour ceux que la puissance d'un point par rapport à un cercle n'inspire pas trop , on peut aussi remarquer que les quatre triangles rectangles sont semblables 2 à 2 ( en observant les angles ) et on retrouve le 4 manquant .
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









