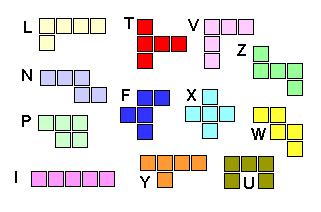|
#1 - 13-06-2017 18:08:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtzau 135
Mon pâtissier m'a posé une petite colle sympa que je vous transmets à mon tour .
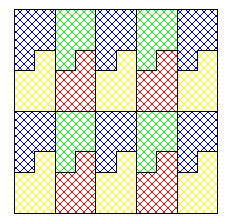
Il m'a montré un petit gâteau carré de 7 cm de côté soigneusement découpé en 7 parts de même volume , comme toujours il a été hyper économe dans les coupes . En plus il applique des règles strictes : il coupe parallèlement aux bords avec des segments de coupe entiers ( en centimètres ) .
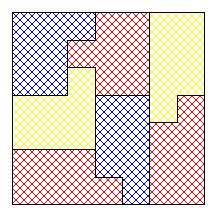
C'est pas jojo mais pas désagréable et ça remplit le cahier des charges 
Il aimerait bien découper un carré de 10 cm de côté en vingt parts égales avec le même cahier des charges . Il y arrive mais uniquement avec des parts identiques ce qui égratigne un peu sa fantaisie : on l'aide ou on le décourage ?
Vasimolo
#2 - 13-06-2017 23:36:04
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
âteau 135
Je ne comprends pas. Si je reformule ton problème plus mathématiquement, tu cherches à découper un quadrillage 10x10 en 20 pentaminos. Comme il n'y a que 12 pentaminos différents, ça parait impossible de ne pas faire deux parts identiques. À moins que tu acceptes les parts dont la connexité ne tient qu'à un sommet ?
Il ne manquerait pas une donnée à ce problème ?
#3 - 14-06-2017 12:07:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gââteau 135
Les parts ne doivent pas être toutes identiques mais deux parts ont le droit de l'être .
Vasimolo
#4 - 14-06-2017 13:33:36
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteaau 135
C'est facile.
On fait 10 double-parts rectangulaires identiques 2x5 par exemple, et on coupe chacune en deux avec deux pentagones identiques tête-bêche ayant 5 angles droits dont un rentrant. (comme les deux de droite sur la figure de l'énoncé)
Il y a une infinité de façons de le faire.
EDIT
Il y a deux façons hors symétries de remplir les double-parts
avec des coupes à coordonnées entières
1) 2 fois 5x1
2) 2 pentagones concaves d'aire 5 :
*** et **
** ***
#5 - 14-06-2017 13:54:09
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
gâreau 135
Bonjour,
il n'y a que deux paires de parts superposables (sans compter les retournements).
Ce gâteau contient les 18 pièces possibles avec 5 carrés
#6 - 14-06-2017 14:07:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâetau 135
Halloduda & Caduk : vous avez oublié une des conditions du partage 
Vasimolo
#7 - 14-06-2017 14:26:27
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâtea 135
C'est impossible.
Le nombre de découpes est égal à la somme des périmètres des pièces, moins le périmètre du carré (pièce unique), le tout divisé par 2 (traits communs à 2 pièces.)
Le seul pentamino de périmètre minimal est un carré de 2 x 2 avec une case sur le côté.
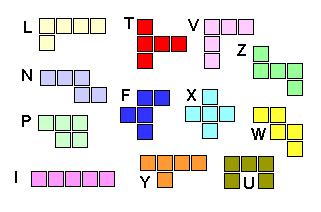
L'ajout d'un pentamino autre augmente le nombre de coupes.
Sauf si on considère que les deux pièces symétriques (sans retournement) sont différentes parmi les 18 pentaminos possibles sans retournement..
Les pièces seront donc toutes de type P
#8 - 14-06-2017 14:59:21
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gâteau 35
Ah oui, il faut minimiser la longueur de coupe...
La longueur de coupe est égale à ∑Pi−402 ou P_i est le périmètre de la pièce. La pièce ayant le plus petit périmètre, 10, est celle composée d'un carré de 2x2 collé à un petit carré. C'est la seule, les autres possèdent un périmètre de 12.
Comme il est possible d'effectuer un partage uniquement avec cette pièce, on ne pourra pas faire mieux en utilisant d'autres pièces.
#9 - 14-06-2017 15:59:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
GGâteau 135
Joli doublé de Gwen & Caduk 
Vasimolo
#10 - 14-06-2017 18:54:01
- Fito11235
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 173
Gâteau 153
Bonjour,
On va l'aider notre bon pâtissier.
Mais 2 parts superposables par retournement sont-elles considérées identiques?
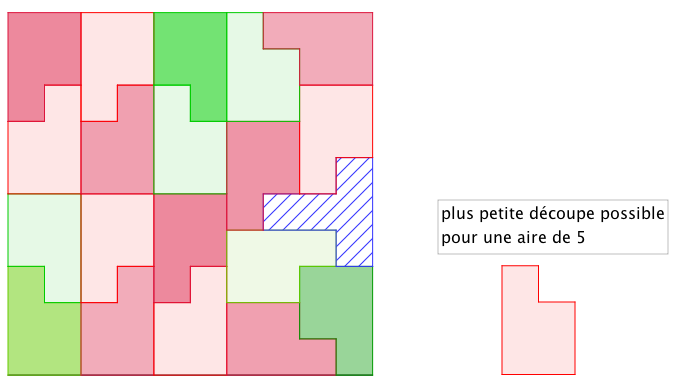
Si c'est le cas, il faut incorporer une forme différente de celle à droite qui a une découpe minimale.
Sinon, je dois réviser ma copie.
Merci.
Fito.
#11 - 14-06-2017 19:03:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtezu 135
Oui Fito , bien sûr deux parts symétriques sont considérées comme identiques .
Vasimolo
#12 - 14-06-2017 23:26:02
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâtrau 135
OK.
Si les 20 parts ont des bords de longueurs respectives b1, b2,..., b20, alors la longueur totale des traits de découpe vaut (b1+b2+...+b20-40)/2 : on enlève 40 car il s'agit de la longueur totale des bords du carré, et on divise par 2 car chaque trait de découpe est le bord de deux parts différentes.
Il existe 12 pentaminos, chacun d'eux a un bord de longueur 12, sauf un, dont la longueur est 10 : s'il respecte sa condition d'économie dans les coupes, il ne pourra utiliser que ce pentamino.
#13 - 15-06-2017 11:00:42
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gteau 135
Bonjour à tous,
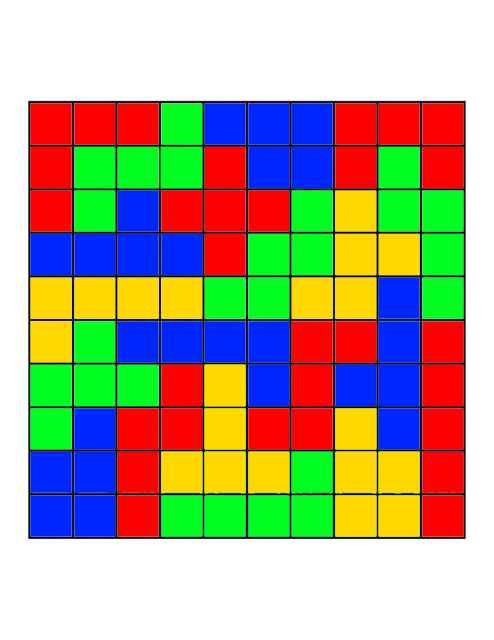
Voici ma proposition:

#14 - 15-06-2017 11:57:15
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
fâteau 135
Si je comprends bien, géométriquement il existe probablement plusieurs solutions, mais dont une seule comporte une longueur de coupe minimale. Est ce bien exact ?
#15 - 15-06-2017 13:04:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâteay 135
@Ebichu : bien 
@Looozer : ta coupe n'est pas minimale .
@Franky : il y a plusieurs coupes minimales , peut-on en trouver une avec au moins deux parts différentes ?
Vasimolo
#16 - 15-06-2017 13:58:00
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
fâteau 135
J'avoue que ton énigme m'a laissé très perplexe depuis le début... 
Si il faut lire :
Il y arrive mais uniquement avec des parts toutes identiques ce qui égratigne un peu sa fantaisie.
alors le partage suivant devrait te convenir  ! !
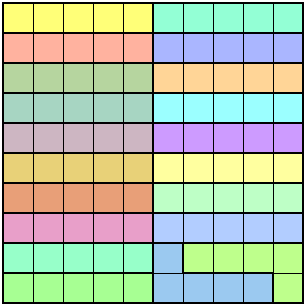
Si par contre tu voulais dire :
de manière qu'Il existe au moins une part qui ne soit pas identique à autre
alors, je n'ai pas de solution et je ne pense pas qu'il y en ait, mais il aurait fallu l'exprimer clairement dès le départ  ! !
#17 - 15-06-2017 14:19:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
fâteau 135
Tu avais bien compris dès le départ mais tu as oublié une des contraintes de l'exercice ( ton exemple n'est pas recevable ) .
Vasimolo
#18 - 15-06-2017 18:30:53
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
âteau 135
Peut-être fais-tu allusion au "comme toujours il a été hyper économe dans les coupes."
Dans ce cas, tous les pentaminos ont une circonférence de 12 unités, sauf un seul de dix.
Il faut donc en employer un maximum de cette sorte. si on veut qu'il y en ait au moins un sans frère jumeau, je ne pense pas que l'on puisse faire l'économie d'employer moins de trois pentaminos de douze unités.
Ce qui pourrait donner cette découpe (mais il en existe sans doute pas mal d'autres) :
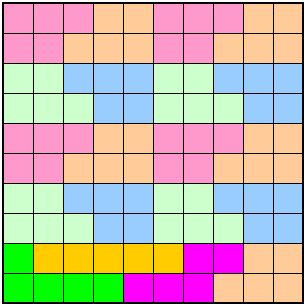
PS : Par contre si on accepte des frères jumeaux, on peut se contenter de deux pentaminos en L (à douze unités), que l'on place tête bêche.
Spoiler : [Afficher le message] J'ai la flemme de refaire un dessin, et je trouve que le problème est un peu moins intéressant que celui avec ma deuxième contrainte.
#19 - 15-06-2017 18:59:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâyeau 135
Tu dois pouvoir faire avec seulement deux pentaminos de 12 en laissant tomber la contrainte d'économie des coupes , mais c'est un impératif premier ...
Vasimolo
#20 - 16-06-2017 01:39:52
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
âGteau 135
Un autre essai (à 13 coupes si j'ai bien compris la contrainte).

#21 - 16-06-2017 18:12:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
|
 |

 Accueil
Accueil
 Forum
Forum