Enigme Gâteau 99 @ Prise2Tete

Vasimolo · #1

Bonjour à tous

Toujours pour illustrer les grands théorèmes mathématiques pour les gourmands , mon pâtissier s‘est attaqué à l’inégalité isopérimétrique qui affirme que tout lacet de longueur P et d’aire A se voit soumis à l’infâme règle : P²/A >= 4.pi . L’égalité ne pouvant être atteinte que par un lacet circulaire .

Si P²/A est entier il est alors supérieur à 12 .

Voici la version « gâteau » de mon pâtissier avec ses gaufrettes carrées :

Le périmètre ( en jaune ) est d’un seul tenant et chaque case du périmètre a exactement deux voisins dans le périmètre . L’aire ( en rouge ) est le nombre de cases cernées par le périmètre . Ici le rapport P²/A = 54 est très peu performant .

Le gâteau ci-dessous est impossible à cause des cases pointées en bleu et vert .

Voilà ce que propose mon pâtissier :

Selon lui c’est la façon la plus économiquo-esthétique d’atteindre le plus petit entier P²/A réalisable .

Quelles sont les dimensions de ce gâteau ?

Peut-on faire mieux en oubliant l’esthétique ?

Amusez-vous bien

Vasimolo

shadock · #2

Tu peux me redonner le logiciel que tu utilises pour tes dessins mon ordi a planté il y a quelques semaines...

Vasimolo · #3

@Shadock : j'utilise le logiciel libre "Declic" http://emmanuel.ostenne.free.fr qui n'est malheureusement plus mis à jour depuis plusieurs années .

Vasimolo

golgot59 · #4

Salut !

Je trouve A=x²+4x en posant x=petite longueur rouge
Et P=4x+12

Du coup, P²/A ne fait jamais un nombre entier...

Aurai-je manqué ou mal compris quelque chose ?

rij99 · #5

Je propose ceci pour la 1ère question.

n ~ 34,439

P ~ 141,756

A ~ 1182

L'entier en question est 17.

rij99

halloduda · #6

Le "périmètre" tel que décrit ici vaut 4(h-1)(l-1), h et l désignant la hauteur et la largeur hors tout, marge comprise.
Un gâteau carré de côté (interne, sans la marge) n a pour périmètre p=4(n+1) et pour aire A=n².
Le rapport p²/A, minimal avec cette forme, est supérieur à 16.
Pour la plus petite valeur entière, 17, le gâteau a pour côté 33>32.49.
(désolé pour le Latex qui aurait permis d'écrire la valeur exacte)
A=1089 ; 17*A=18513
p=4*34=136 ; p²=18496
p²/A=16.984...
Il suffit de retirer 18513-18496 = 17 carrés 1x1 dans les coins pour réduire l'aire et obtenir p²/A=17,
et non pas 4 comme suggéré dans l'énoncé.

Franky1103 · #7

Soient M et N les dimensions du rectangle dans lequel le gâteau s’inscrit.
On a: P(C) = 2.(M-1) + 2.(N-1) = 2.(M+N-2) et A(C) = (M-2).(N-2) - 4 = MN - 2.(M+N)
En balayant toutes les valeurs de M et N inférieures à 100 avec un tableur, j’obtiens une valeur minimale de P²/A de 18 pour trois gâteaux différents: 20 x 21; 21 x 24 et 24 x 35, ce qui ne constitue bien sûr pas une démonstration rigoureuse.
Quant à une possible amélioration, je pense à ajuster au plus près le gâteau dans un cercle, mais je n’ai pas encore abouti ma réflexion.
I’ll be back.

Vasimolo · #8

@Golgot : c'est possible .
@Rij et Halloduda : les gaufrettes et le rapport P²/A doivent être entiers .
@Franky : on peut faire mieux .

Deux petits points de détail :

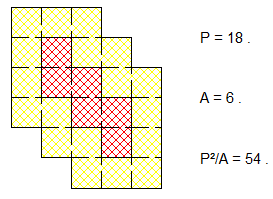
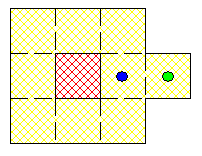
On appelle périmètre du gâteau le nombre de cases jaunes ( ce n'est donc pas le périmètre au sens usuel ) , je pensais que c'était clair sur l'exemple .

Une fois le minimum trouvé pour le rapport P²/A ( qui doit être entier ) , il faut réaliser un gâteau illustrant ce minimum avec le moins de gaufrettes possible . Je ne l'avais pas préciser mais les gaufrettes doivent être entières il est donc interdit de les couper ou de les casser .

J'espère que c'est plus clair , n'hésitez pas à poser des questions ou à demander plus de temps si nécessaire .

Amusez-vous bien .

Vasimolo

gwen27 · #9

Ce qu'il propose est impossible avec un rapport entier.

La limite est 16, je pense , mais jamais atteinte.

On a 17 pile en retirant juste un des coins du carré rouge de dimension 33.

Vasimolo · #10

La borne est bonne Gwen mais l'exemple n'est pas correct .

Je rappelle que le périmètre est le nombre de gaufrettes jaunes .

Vasimolo

gwen27 · #11

Si, le compte est correct.

( 33 x 33 ) -1 = 1088 pour l'aire en rouge

(33 x 4 + 4 )^2 = 18496

18496/1088 = 17

Vasimolo · #12

Au sens du pâtissier ton périmètre fait 128 ( c'est le nombre de gaufrettes jaunes ) .

Vasimolo

gwen27 · #13

Désolé de ne toujours pas être d'accord. Ca fait bien 136.

Franky1103 · #14

J'avais compris (peut-être à tort) que les quatre coins du gâteau étaient "cassés" de façon identique. Par ailleurs, je peux démontrer qu'un gâteau inscrit dans un carré ne satisfait pas aux conditions demandées. J'étais donc parti sur un gâteau inscrit dans un rectangle, mais je n'arrive pas à descendre en dessous de 18 pour P²/A, alors que Vasimolo m'indique qu'on peut faire mieux. Pour mémoire:
- gâteau 20x21: P=78 et A=338 => A=18
- gâteau 20x24: P=84 et A=392 => A=18
- gâteau 24x35: P=114 et A=722 => A=18

Vasimolo · #15

D'accord Gwen je m'étais emmêler avec les carrés rouge et jaune

La solution du pâtissier propose 4 axes de symétries ( quelle est-elle ?) , la tienne plus économique n'en présente qu'un : on peut faire aussi bien avec le même nombre de gaufrettes et deux axes de symétrie .

Vasimolo

gwen27 · #16

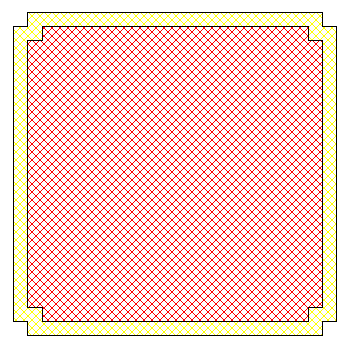
Un simple rectangle rouge de 32 x 34

Vasimolo · #17

Eh oui , bien joué Gwen .

Vasimolo

Franky1103 · #18

Je viens de voir un truc. Le périmètre, en nombre de gaufrettes jaunes, est toujours égal au rectangle circonscrit au gâteau rouge. Tant qu'à optimiser, autant remplir directement ce rectangle circonscrit de gaufrettes rouges, puisque l'aire est au dénominateur. Ainsi la valeur minimale du rapport P²/A est forcément obtenue à partir d'un simple rectangle, non ?

Vasimolo · #19

Oui , la contrainte principale est P²/A entier , sinon on peut approcher le 16 autant qu'on le souhaite .

Vasimolo

golgot59 · #20

Ah, il me semblait bien que c'était impossible d'obtenir un tel gâteau "carré"!!!

Dommage, du coup je n'ai pas cherché plus loin en pensant que ne passant déjà pas l'étape 1...

Franky1103 · #21

Dans le cas d’un carré (forme la plus "compacte"), la valeur de P²/A tend vers 16 sans jamais l’atteindre. Donc le rapport entier P²/A optimal est 17. Le carré dont le P²/A est immédiatement inférieur à 17 (sans tenir compte d’être entier) est le 33 x 33. Pour rendre ce rapport entier, j’enlève autant de gaufrettes rouges que nécessaire sans changer le périmètre: ici en enlever une seule suffit et on obtient le gâteau de gwen27 du post #13. Si on veut en faire un rectangle, on déplace une rangée de 32 gaufrettes d’un côté sur l’autre et on obtient le gâteau de gwen27 (encore lui ) du post #16. On ne peut pas faire mieux. Désolé d’avoir refait cette énigme après coup .

nodgim · #22

Idem pour moi, je ne voyais qu'un carré, et bien sûr pas de solution entière.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 13-06-2015 12:29:08

Gâteau 999

#0 Pub

#2 - 14-06-2015 17:40:33

Gâteau 999

#3 - 14-06-2015 18:37:58

Gâteeau 99

#4 - 14-06-2015 22:49:32

Gtâeau 99

#5 - 15-06-2015 11:22:03

hâteau 99

#6 - 15-06-2015 12:14:15

gâteay 99

#7 - 15-06-2015 15:03:38

Gâteau 999

#8 - 15-06-2015 17:09:36

gâteay 99

#9 - 15-06-2015 19:36:06

Gâteau 9

#10 - 15-06-2015 21:22:49

âGteau 99

#11 - 15-06-2015 21:50:59

gâtezu 99

#12 - 16-06-2015 10:27:12

gâtzau 99

#13 - 16-06-2015 13:09:49

Gâteeau 99

#14 - 16-06-2015 15:05:08

Gâteau 9

#15 - 16-06-2015 17:42:42

gâreau 99

#16 - 16-06-2015 18:22:08

âGteau 99

#17 - 16-06-2015 18:51:39

gâyeau 99

#18 - 16-06-2015 18:54:26

fâteau 99

#19 - 16-06-2015 19:10:06

Gâtteau 99

#20 - 16-06-2015 19:46:34

Gâetau 99

#21 - 16-06-2015 21:03:39

Gtâeau 99

#22 - 17-06-2015 08:04:16

Gâtea u99

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums