|
#1 - 20-09-2015 17:56:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 21-09-2015 07:45:54
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâtaeu 106
Bonjour à tous,
Imaginons le plus mauvais scénario pour le pâtissier.
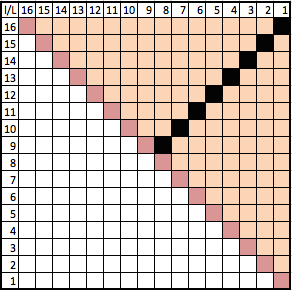
Pour que deux gaufrettes rectangulaires de dimensions entières ne puissent être superposées sans débordement, il faut que l'une soit supérieure en longueur et que l'autre soit supérieure à la en largeur.
Avec des entiers entre 1 et 16, on peut faire un maximum de telles paires en prenant : 16-1; 15-2; 14-3; 13-4; 12;5; 11-6; 10-7 et 9-8
Avec 3 fois ce jeu de gaufrettes (soit 24 gaufrettes), seules les pièces identiques pourront être empilées on pourra alors atteindre au maximum un empilement de 3 pièces.
Une 25ème gaufrette aura, soit une forme identique à un trio déjà existant, soit des dimensions lui permettant de supporter ou d'être superposée à un trio de pièces identiques.
Donc je dirais que c'est Ok pour le pâtissier.
#3 - 21-09-2015 08:36:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
fâteau 106
Je suppose que tu parles de 25 gaufrettes toutes de tailles différentes ? Car affleurer n'est pas déborder. Et sans doute tu parles de 4 gaufrettes prises au hasard, auquel cas on pourrait empiler les 25 ?
#4 - 21-09-2015 13:23:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteu 106
@Looozer : C'est sûrement le bon angle d'attaque mais il faudrait justifier pourquoi la position considérée est la "pire" 
@Nodgim : le problème n'est pas dans ce sens . Les 25 gaufrettes sont données au hasard parmi toutes les gaufrettes possibles ( on pourrait avoir 25 fois la même ) . Ensuite il faut en choisir 4 dans le lot et les empiler comme demandé . Peut-on envisager un lot de gaufrettes où ce choix est impossible ?
Vasimolo
#5 - 21-09-2015 13:48:18
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
Gâteau 016
Salut
Si j’ai bien compris le problème 
Imaginons 25 gaufrettes identiques, je peux en prendre 4 et les empiler sans qu’elles débordent.
Si maintenant je prends 8 séries de 3 gaufrettes
De 16x1, 15x2, 14x3 etc…. 8x9 soit 24 gaufrettes
Dans cette configuration, je ne peux pas empiler 4 gaufrettes sans débordement
Mais il reste une gaufrette, quelque soit sa dimension, je pourrais la poser soit dessus, soit dessous.
Donc il y aura toujours une possibilité d'empiler 4 gaufrettes.
#6 - 21-09-2015 14:17:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtezu 106
Oui Nobodydy , tu es parti sur la même idée que Looozer , mais qui te dit que cette configuration est la pire possible ?
Vasimolo
#7 - 21-09-2015 15:02:45
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#8 - 21-09-2015 15:48:50
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtteau 106
Pour qu'on ne puisse pas empiler 4 gâteaux, il faudrait déjà qu'avec 24 on ne puisse pas.
On ne peut éviter la condition de 4 superposables que d'une seule façon avec 24 gâteaux. Il faut faire 3 gâteaux de chacune des 8 formes :
16x1, 15x2, 14x3, ..., 9x8.
En effet, on ne peut faire que 8 gâteaux non superposables deux à deux.
Leurs dimensions sont 16x1, 15x2, 14x3, ..., 9x8.
Toute autre forme est soit incluse dans l'un de ces gâteaux ou inclut l'un d'eux.
Le 25ème empiète sur - ou est contenu dans - l'un des 24 existants.
Conclusion : on peut toujours trouver 4 gâteaux empilables sans débordement.
#9 - 21-09-2015 16:26:51
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
gâteai 106
Est ce que tu veux dire qu'on tire 4 gaufrettes au hasard sur les 25 disponibles ?
Il suffirait sinon de choisir les "bonnes" gaufrettes et il n'y aurait plus d'énigme.
#10 - 21-09-2015 16:42:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
âGteau 106
@Franky : les 4 gaufrettes sont choisies mais pas le lot de 25 .
@Nobodydy & Halloduda : Avez-vous montré que le lot de 24 gaufrettes que vous proposez est le seul avec lequel on ne peut pas ériger une pyramide de 4 étages ? Si c'est le cas , le problème est bien sûr résolu 
Vasimolo
#11 - 21-09-2015 19:37:42
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteaau 106
J'ai envie de faire simple :
Chaque gaufrette a une largeur et une longueur et donc 2 dimensions.
Si une même dimension apparaît plus de 3 fois, cela fera plus de 3 gaufrettes superposables.
24 gaufrettes, c'est 24 longueurs et 24 largeurs, soit 48 dimensions.
Au delà, une dimension apparaîtra 4 fois.
Après, on peut supposer qu'une gaufrette est carrée, voire 2 ou même 3 (pas plus car elles seraient empilables) . Admettons...
Mais ça ne change pas le problème, car une gaufrette de dimension n x n au milieu de rectangles stricts est tout à fait équivalente à une gaufrette n x (n+1) à part le cas trivial de 16 x 16. Donc si le problème a une solution avec une gaufrette carrée, il en aurait une avec des rectangles purs.
#12 - 21-09-2015 21:02:19
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 10
Bon, j'imagine que comme tout le monde je suppose que la pire situation est d'avoir 3 gaufrettes de chacune des dimensions suivantes :
1-16
2-15
3-14
4-13
5-12
6-11
7-10
8-9
Et que donc tout autre 25ème permettra de construire la tour.
Mais je n'ai pas non plus la démonstration...
#13 - 21-09-2015 21:28:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 16
@Golgot : oui , tu rejoins les autres 
@Gwen : tu peux clarifier le cas des gaufrettes carrées ?
Vasimolo
#14 - 21-09-2015 21:56:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
GGâteau 106
Si on peut empiler une gaufrette carrée dans une gaufrette rectangulaire, on peut la remplacer par une gaufrette rectangulaire de dimension juste supérieure en largeur ou en longueur.
Donc, si le problème est soluble avec des gaufrettes carrées, cela revient à dire qu'il est soluble avec des gaufrettes rectangulaires uniquement.
Or , je prouve juste avant qu'une solution avec des rectangles stricts est impossible.
Si le carré est de 16 x 16 , on s'en fiche, ou au pire on le remplace par 15 x 16
#15 - 21-09-2015 22:12:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gtâeau 106
Possible avec certaines gaufrettes carrées => possible avec gaufrettes uniquement rectangulaires : d'accord .
Mais sauf erreur , il me semble que le raisonnement que tu utilises fonctionne dans l'autre sens .
J'ai pu raté quelque chose 
Vasimolo
#16 - 22-09-2015 07:46:56
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâtaeu 106
Possible avec certaines gaufrettes carrées => possible avec gaufrettes uniquement rectangulaires
Est équivalent à
"Impossible avec des gaufrettes rectangulaires => impossible avec des gaufrettes carrées"
Je crois que c'est une contaposée, non ?
Cette relation logique permet d'évacuer le cas assez embarrassant des carrés.
On en revient donc au cas assez simple des rectangles :
Une 49e dimension deviendra la quatrième occurrence d'une des mesures et donc 4 gaufrettes seront empilables au moins.
#17 - 22-09-2015 08:12:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteua 106
On peut fabriquer 8 modèles non superposables en 3 exemplaires chacun de demi périmètre 17, soit de 16*1 à 9*8. ça fait 24 gaufrettes avec lesquelles il est impossible de faire un gâteau de 4 gaufrettes superposées. Mais s'il faut une 25ème gaufrette, on ne peut pas l'éviter.
#18 - 22-09-2015 08:23:41
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteau 1006
@Nobodydy & Halloduda : Avez-vous montré que le lot de 24 gaufrettes que vous proposez est le seul avec lequel on ne peut pas ériger une pyramide de 4 étages ? Si c'est le cas , le problème est bien sûr résolu 
Vasimolo
On peut faire 136 différentes tailles de gaufrettes rectangulaires.
1≤x≤y≤16.
L'étude exhaustive est vite faite, ou me trompé-je ?.
#19 - 22-09-2015 13:17:15
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâtzau 106
Notons ( Li, li ) les dimensions de la gaufrette i
Classons les 25 gaufrettes par longueur décroissante et en départage par largeur croissante.
Raisonnons par l'absurde en considérant que ces 25 gaufrettes ne "fonctionnent" pas, et remplaçons les 3 premières gaufrettes par (16,1)
On voit clairement que cette configuration ne "fonctionne" pas non plus (Il ne peut pas y avoir une 4eme gaufrette de longueur 16 ni de largeur 1 sinon ça "fonctionnerait" et dans le cas contraire, les 3 gaufrettes initiales ne peuvent pas "servir" vu que les autres ont une taille (<16,>1) et ne sont pas compatibles
On recommence le process de substitution en remplaçant les 3 prochains par (15,2) puis (14,3 )... jusqu'à (9,8) en remarquant les même notions d'incompatibilité entre les différents paquets.
Il reste une gaufrette dans cette nouvelle configuration que nous avons montré être plus défavorable que l'initiale.
Cette dernière gaufrette a une longueur >=9 ou un largeur <8 et on peut donc l'ajouter a un paquet de 3 gaufrettes identiques dont il aura la même longueur ou même largeur et qui formera un quartet gagnant.
La solution modifiée fonctionne donc ce qui contredit l'hypothèse initiale.
De manière générale avec des gaufrettes de taille maximum M et en voulant empiler P gaufrettes
si M pair il faut au minimum M/2 * P + 1 gaufrettes
Si M impair il en faut (M+1) /2 * P + 1 gaufrettes (la "transformée" acceptant un carré)
Edit 1 : il manquait le 2 apres le / dans "Si M impair il en faut (M+1) /2 * P + 1 gaufrettes (la "transformée" acceptant un carré)"
Nota bene : Ce raisonnement est en effet probablement artificiellement alourdi et il n'est peut être pas indispensable de passer par un raisonnement par l’absurde dont je ne sus pas certain que cela en soit un.. J'ai essayé de simplifier mais je me heurte au problème des carrés qui semblent poser des difficultés aux posteurs... C'est d'ailleurs le fait, quand la longueur max est impaire, qui fait apparaître le carré final et crée le +1 dans la formule.
#20 - 22-09-2015 17:41:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#21 - 22-09-2015 19:32:42
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
âteau 106
Bon, je me lance (de là à dire que je vais me ramasser !  ) )
Le pire des cas, pour moi, ce serait d'avoir des gaufrettes de dimensions 1*16, 2*15, 3*14... 7*10 et 8*9... Aucune de ces 8 gaufrettes ne peut se superposer. Je n'ai pas trouvé de démonstration immédiate, mais quelques traits de crayon semblent bien montrer qu'on ne peut gérer à la fois longueur et largeur.
Mais toute autre gaufrette sera superposable (ou sous-posable si j'ose dire) avec au moins l'une d'entre elles. Une gaufrette 5*14 pourra aller sous la 3*14 ou sous la 5*12. Il n'en faut pas + de 2, sinon on a notre pyramide de 4 gaufrettes.
Une gaufrette de 6*13 n'est plus insérable sous la 5*12. De même, il n'en faut pas plus de 2...
On pourra donc, au pire, avoir 8 pyramides de 3 gaufrettes, + 1 gaufrette qu'on pourra également insérer dans une des ces pyramides. Etant entendu que des gaufrettes de mêmes dimensions sont superposables.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#22 - 22-09-2015 19:41:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 10
Ben oui Fix , tu es comme tout le monde , tu as mis le doigt sur la position critique . Après il faut justifier et là c'est fatiguant 
Vasimolo
#23 - 22-09-2015 23:30:17
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâeau 106
Considérons la gaufrette l*L, avec l+1<L, entiers > 0 et < 17.
(l+1)*(L-1) = l*L + L-l -1 > l*L
Donc la gaufrette l*L ne peut être posée qu'au-dessus d'une gaufrette (l+1)*(L-1).
Ne "suffirait"-il pas de prouver que ?
L^2 > (l+1-a)^2 + (L-1-b)^2, pour tout a et b réels positifs tels que a^2 + b^2 = 1.
La quantité de droite étant le carré de la plus longue gaufrette de côté 1 pouvant être superposée à la gaufrette (l+1)*(L-1), et la quantité de gauche étant le carré de la longueur de notre gaufrette qu'on voudrait bien placer dessus...
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#24 - 23-09-2015 18:05:26
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâteua 106
Juste une remarque. Contrairement a ce que beaucoup disent 16-1 ...9-8 n'est pas LA seule solution a 24 gaufres. Remplacer 9-8 par 99 ou 88 donne le méme résultat (contrairement au cas ou la longeur maxi est impaire car là, on est forcé de mettre un carré si on veut "optimiser" la structure et cette dois il n'y a pas de choix.)
#25 - 23-09-2015 19:02:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
gâtzau 106
  
Je comprends rarement tes problèmes du premier coup... et il faut toujours que je m'explique 2 fois.
Etape 1 : 25 rectangles stricts donnent 50 dimensions différentes 2 à 2 dans les rectangles. Ce qui veut dire que parmi les 16 dimensions possible, il y en a au moins 1 qui revient plus de 3 fois. Donc, on pourra toujours empiler 4 formes vu qu'elles ont la même longueur ou la même largeur
Etape 2 : Je vais varier un peu pour plus de clarté.
Bon, un dessin :
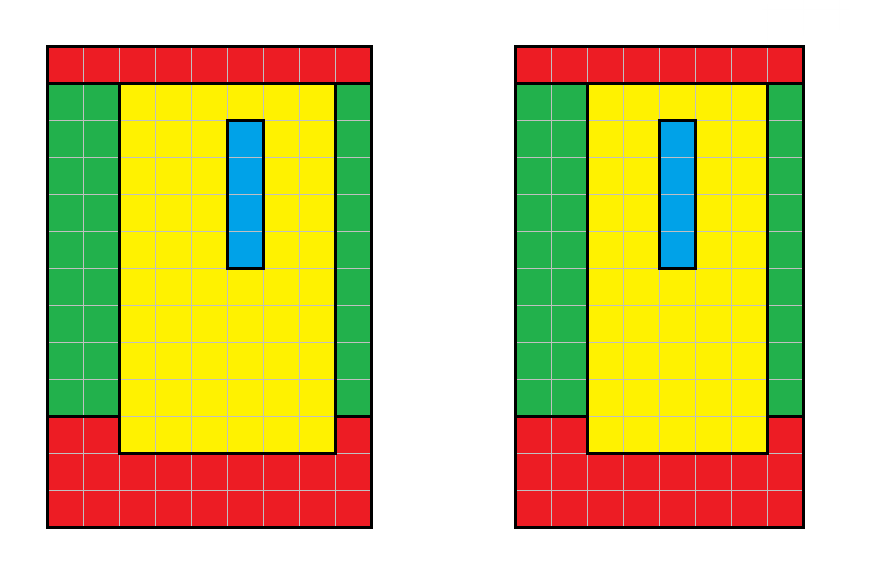
Hypothèse :
Admettons qu'un jeu de 25 formes (carrés possibles) ne permette pas de superposer 4 des formes...
Imaginons que , à part les pièces de largeur 1, on diminue la largeur de chaque pièce de 1 unité.
Cela ne change strictement rien aux possibilités de superposition quelles que soient les pièces choisies.
Ah, oui, il reste le cas du carré 1 x 1 , transformons le en 2 x 1.
On a donc construit un lot de 25 rectangles stricts qui n'autorise aucune superposition de 4 pièces.
Donc, si un jeu de 25 rectangles dont des carrés ne permet pas de superposer 4 formes, alors je peux trouver un jeu de 25 rectangles stricts qui ne le permette pas non plus....
Etape 3 : Vu la conclusion du 1, l'hypothèse du 2 est impossible.
|
 |

 Accueil
Accueil
 Forum
Forum







.png)
.png)