Les cercles ont le même centre et selon la coutume, les croix rouges signifient des longueurs égales .

Vasimolo

A première vue, je dirais que c'est impossible. sauf si la distance rouge est nulle.

Ca n'est pas une intuition...

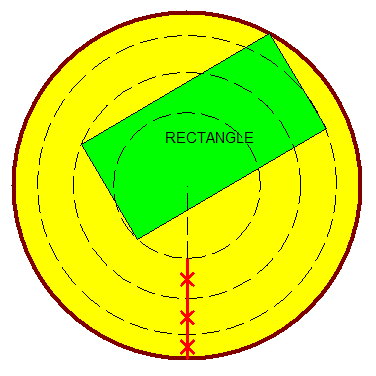
On pose un point dans le plan distant des sommets du rectangle de A, A+x, A+2x, A+3x.
La distance de ce point aux 4 cotés du rectangle est a,b,c,d.
On pose 4 équations de Pythagore
(1) a²+b²=A²
(2) b²+c²=(A+x)²
(3) a²+d²=(A+2x)²
(4) c²+d²=(A+3x)²
(2)-(1)+(3) aboutit à l'équation c²+d²=A²+6Ax+5x²
A comparer avec l'équation (4) qui mène à poser
(A+3x)²=A²+6Ax+5x².

il faut x=0.
On ne peut pas faire un gâteau comme ça.

Soient (C1), (C2), (C3) et (C4) respectivement les cercles du plus petit au plus grand. Leur centre commun est noté O
Dans un repère orthonormé de centre O (dont on positionnera les axes parallèles aux côtés du rectangles pour simplifier les calculs), les équations des cercles sont:

- (C1): x^2+y^2=r^2

- (C2): x^2+y^2=(r+k)^2

- (C3): x^2+y^2=(r+2*k)^2

- (C4): x^2+y^2=(r+3*k)^2

où r est le rayon de (C1) et k l'écart entre les rayons.

Nommons le rectangle ABCD avec A sur (C1), B sur (C2), C sur (C4) et D sur (C3).

Soient L et l les côtés de ABCD. Si A(a,b) alors B(a,b+l), C(a+L,b+l) et D(a+L,b).

En introduisant les cordonnées de ces points dans les équations de leurs cercles, on a:
* A sur (C1): a^2+b^2=r^2 (1); cette relation sera utilisée pour la suite.

* B sur (C2): l^2 +2*b*l=2*k*r+k^2 (2)

* C sur (C4): L^2+l^2+2*a*L+2*l*b=9*k^2+6*k*r (3)

* D sur (C3): L^2+2*a*L=4*k*r+4*k^2 (4).

En additionnant membre par membre les équations (2) et (4) on a:

(l^2 +2*b*l) + (L^2+2*a*L) = (2*k*r+k^2) + (4*k*r+4*k^2)

soit : L^2+l^2+2*a*L+2*b*l = 6*k*r+5*k^2 (5)

Les membres de gauche des équations (3) et (5) sont égaux donc les membres de droite le sont aussi; soit : 9*k^2+6*k*r = 6*k*r+5*k^2. On en déduit que 9*k^2=5*k^2 donc k=0

La réalisation de ce gâteau est donc impossible sauf d'avoir les 4 cercles de même dimension.

Voilà... sauf si une erreur s'est glissée quelque part

Soit ABCD le rectangle centré sur O dans un un repère orthonormé. Les coordonnées des sommets de ce rectangle sont: A(-a;-b); B(-a;+b); C(+a;+b); D(+a;-b) et ceux du centre du cercle concentrique (x0;y0).
A appartient au cercle de rayon R => (a+x0)² + (b+y0)² = R² (1)
B appartient au cercle de rayon R+r => (a+x0)² + (b-y0)² = (R+r)² (2)
C appartient au cercle de rayon R+3r => (a-x0)² + (b-y0)² = (R+3r)² (3)
D appartient au cercle de rayon R+2r => (a-x0)² + (b+y0)² = (R+2r)² (4)
(1) et (2) donnent: -4by0 = r(2R+r); (3) et (4) donnent: -4by0 = r(2R+5r)
d’où: r(2R+r) = r(2R+5r) => r=0
Je trouve donc que les cercles doivent tous avoir le même rayon: c’est étonnant.

C'était donc impossible

Pas grand chose à ajouter aux démonstrations déjà produites .

Merci aux participants .

Vasimolo

J'ai eu une piste sans calcul que je n'ai pas réussi à suivre... Fausse piste ou pas ?

Si on réduit les distances on arrive à 0 x 2x 3x  soit le début d'un genre de spirale c e qui ne peut pas donner de rectangle.

Mais cette réduction se fait depuis le centre des cercles. Depuis le centre du rectangle on est sensé avoir toujours un rectangle. Je n'ai pas réussi à passer de l'un à l'autre ce qui serait un contresens et donc, une impossibilité.