Si je ne m'abuse, on ne peut pas faire mieux que 4 côtés.

Le point clé du raisonnement consiste à se placer en un sommet du polygone où il y a un angle obtus (ce qui existe obligatoirement si le polygone a au moins 5 côtés).

J'essaierai de détailler mon raisonnement demain avec des figures, mais je distingue deux cas : un plutôt facile, lorsqu'aucun des côtés de l'angle obtus n'est horizontal ou vertical, et l'autre qui est un peu plus casse-pieds, mais on s'en sort quand même.

J'ai un peu de mal à imaginer qu'il existe une feuille de menthe convexe à plus de quatre côtés satisfaisant à ces contraintes: wait and see.

Ça y est, j'ai finalisé mon raisonnement, ça n'a pas pris la direction que je pensais finalement. Ça n'utilise rien de compliqué, mais ça n'est pas "très simple", il doit y avoir mieux...



Supposons que l'on dispose d'un polygone qui vérifie les conditions de l'énoncé. On va montrer qu'il a au plus 4 côtés.

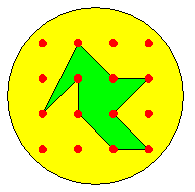
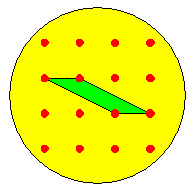
Alors, on considère trois sommets A, B, C consécutifs de ce polygone, joints par deux arêtes dans ce polygone. Par exemple, sur la figure de gauche, c'est le cas des trois sommets et des deux arêtes en rouge.

Il n'y a pas de point du réseau à l'intérieur du triangle, car il n'y en a pas dans le polygone. De plus, ou bien le polygone est précisément ce triangle, ou bien il n'y a pas de point du réseau sur le segment [AC]. Par contre, il peut y avoir un ou plusieurs points du réseau sur [AB] (j'en ai mis un sur l'exemple, en noir), ou sur [BC], mais pas sur [AB] et [BC] en même temps, car sinon il y aurait un point du réseau à l'intérieur du triangle ou sur le segment [AC].

Dans la suite, s'il y a des points du réseau sur [AB] ou [BC], par exemple [AB], on considère le triangle A'BC, où A' est le point noir le plus proche de B (voir figure du milieu). Alors, il n'y a pas de point du réseau dans A'BC, car il est inclus dans ABC, ni sur ses arêtes. Il n'y a donc pas non plus de point du réseau à l'intérieur du parallélogramme de la figure du milieu par symétrie (ni sur ses arêtes), ni à l'intérieur de la figure de droite par translation.

Dans la figure de droite, demandons-nous maintenant quels points du réseau peuvent être des sommets du polygone ? Déjà, pas ceux situés strictement en-dessous du grand "V", sinon le polygone ne serait pas convexe. Ni ceux situés strictement au-dessus du grand "V", sinon le sommet vert serait à l'intérieur du polygone. Les sommets en bleu sont éliminés par convexité.

Il ne reste que les sommets noirs ou verts. Mais dès lors qu'on en choisit un en tant que sommet supplémentaire du polygone, tous les autres sont éliminés : le polygone est au plus un quadrilatère.

Ha oui, crotte, j'avais mal lu l'énoncé, désolé Je la refais mais sans la "variante Ebichu". C'est déjà plus simple.



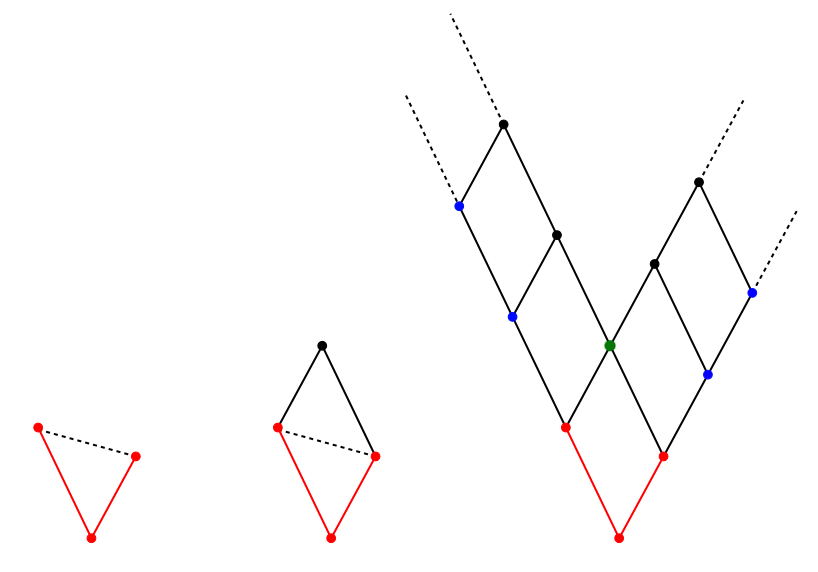
Supposons que l'on dispose d'un polygone qui vérifie les conditions de l'énoncé. On va montrer qu'il a au plus 4 côtés.

Pour cela, on considère trois sommets consécutifs de ce polygone, joints par deux arêtes dans ce polygone. Par exemple, sur la figure de gauche, c'est le cas des trois sommets et des deux arêtes en rouge.

Il n'y a pas de point du réseau à l'intérieur du triangle (ni sur ses arêtes), car il n'y en a pas dans le polygone. Il n'y a donc pas non plus de point du réseau à l'intérieur du parallélogramme de la figure du milieu par symétrie, ni à l'intérieur de la figure de droite par translation.

Dans la figure de droite, demandons-nous maintenant quels points du réseau peuvent être des sommets du polygone ? Déjà, pas ceux situés en-dessous du grand "V" (points bleus y compris), sinon le polygone ne serait pas convexe. Ni ceux situés au-dessus du grand "V" (points noirs y compris), sinon le sommet vert serait à l'intérieur du polygone.

Seul le sommet vert peut appartenir au polygone, qui est au mieux un quadrilatère. En cadeau : si c'est un quadrilatère, alors c'est un parallélogramme.

Je vais plutot chercher a montrer l'impossibilité dans ce cas..

Si je prends 4 points (3 côtés du polygone )
Les 2 extrémités sont en violet.


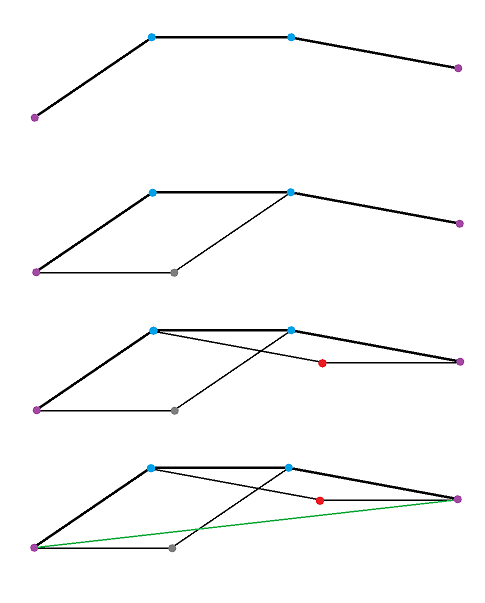
Je peux construire un paralellogramme  avec deux côtés adjacents.

Cela crée deux points (gris et rouge) qui sont des mailles.

Ces deux points forment eux même un paralellogramme avec les deux points violets, et celui-ci a donc une diagonale (verte) qui laisse un des deux points créés dans le quadrilatère bleu et violet.

Si je veux mettre un point de plus à cette figure, soit il est sous le trait vert, mais elle contient la maille rouge, soit il est au-dessus, mais la figure est concave.

Oui, avec les deux indices, d'accord... Spoiler : [Afficher le message] Le milieu de deux points du réseau est lui-même un point du réseau si et seulement si la différence entre les abscisses de ces deux points et la différence entre les ordonnées de ces deux points sont paires.

Ainsi on peut répartir les points du réseau en 4 classes : ceux dont les coordonnées sont (pair;pair), ou (pair;impair), ou (impair;pair) ou (impair, impair).

En prenant un pentagone, il y aura forcément 2 sommets dans la même classe (tiroirs), donc leur milieu sera un point du réseau à l'intérieur du pentagone.