|
#1 - 17-02-2015 17:22:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 18-02-2015 13:35:06
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
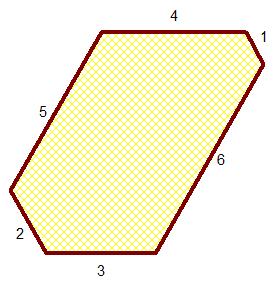
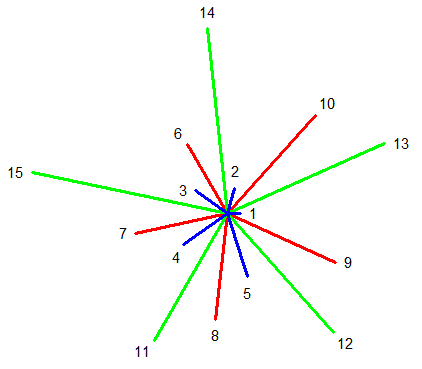
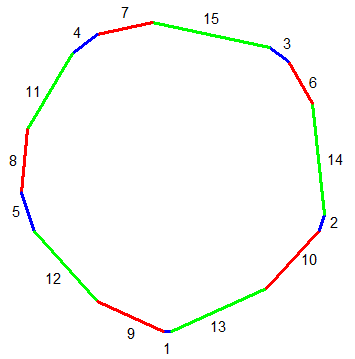
Gâteau 9
Un décagone par exemple (image cliquable) :
#3 - 18-02-2015 15:42:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 9
Parfait Gwen 
Y'en a pas d'autres ?
Là encore il y a une généralisation assez surprenante 
Vasimolo
#4 - 18-02-2015 16:01:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gââteau 94
Bah, pour tous les multiples de deux par un nombre impair , ça marche déjà...
Pour les autres, je ne vois pas. (avec des côtés entiers pas nécessairement tous différents, oui, mais avec des entiers consécutifs, pour l'octogone et l'heptagone, ça parait difficile déjà )
Donc 2x3= 6 2x5 = 10 ça marche facilement, les autres, j'ai un doute même si je ne trouve pas d'astuce pour un ennéagone.
#5 - 18-02-2015 16:23:25
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteu 94
Pour un décagone, mon idée est de remarquer que: cos(72°)=cos(2.pi/5)=(-1+V5)/4, et: cos(36°)=cos(pi/5)=(1+V5)/4, puis d'écrire la somme de la projection de cinq côtés consécutifs et de scinder les parties rationnelle et irrationnelle. Mais je n'ai pas encore abouti: affaire à suivre ...
#6 - 18-02-2015 17:32:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteay 94
@Gwen : pour l'heptagone ça paraît en effet très difficile si on en croit le gâteau précédent 
Vasimolo
#7 - 18-02-2015 17:56:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteai 94
Un dodécagone équiangle dont les côtés sont des entiers consécutifs :
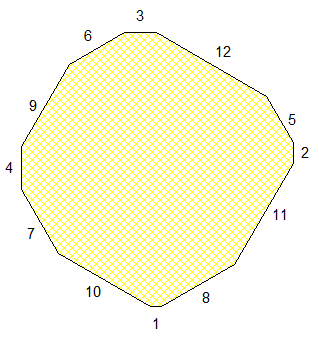
Bien sûr ça ne répond pas à la question , mais ça montre que le problème n'est pas complètement évident 
Vasimolo
#8 - 18-02-2015 20:04:11
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
âGteau 94
Je pense que la figure en question a un nombre pair de côté et que les côtés sont les suivants pour un octogone:
8-1-6-3-7-4-5-2
Il doit probablement y avoir une construction analogue pour le décagone régulier mais comment?
Un promath- actif dans un forum actif
#9 - 18-02-2015 21:02:14
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
âGteau 94
Bonsoir,
J'obtiens 2 hexagones (plus les 2 symétriques)
24 décagones
Code:[1, 4, 5, 8, 9, 2, 3, 6, 7, 10]
[1, 4, 5, 10, 7, 2, 3, 6, 9, 8]
[1, 4, 7, 6, 9, 2, 3, 8, 5, 10]
[1, 4, 7, 10, 5, 2, 3, 8, 9, 6]
[1, 4, 9, 6, 7, 2, 3, 10, 5, 8]
[1, 4, 9, 8, 5, 2, 3, 10, 7, 6]
[1, 6, 3, 8, 9, 2, 5, 4, 7, 10]
[1, 6, 3, 10, 7, 2, 5, 4, 9, 8]
[1, 6, 7, 4, 9, 2, 5, 8, 3, 10]
[1, 6, 9, 4, 7, 2, 5, 10, 3, 8]
[1, 7, 3, 9, 5, 6, 2, 8, 4, 10]
[1, 7, 3, 10, 4, 6, 2, 8, 5, 9]
[1, 7, 4, 8, 5, 6, 2, 9, 3, 10]
[1, 7, 4, 10, 3, 6, 2, 9, 5, 8]
[1, 7, 5, 8, 4, 6, 2, 10, 3, 9]
[1, 7, 5, 9, 3, 6, 2, 10, 4, 8]
[1, 8, 2, 9, 5, 6, 3, 7, 4, 10]
[1, 8, 2, 10, 4, 6, 3, 7, 5, 9]
[1, 8, 3, 6, 9, 2, 7, 4, 5, 10]
[1, 8, 4, 7, 5, 6, 3, 9, 2, 10]
[1, 8, 5, 4, 9, 2, 7, 6, 3, 10]
[1, 8, 5, 7, 4, 6, 3, 10, 2, 9]
[1, 9, 2, 8, 5, 6, 4, 7, 3, 10]
[1, 9, 3, 7, 5, 6, 4, 8, 2, 10] et 732 dodécagones (dont celui de vasimolo #7)
Il est à noter que, pour chaque solution, on en obtient une infinité en augmentant la longueur de chaque côté d'un même nombre entier. Les longueurs sont encore consécutives, mais ne commencent plus à 1, ce qui n'est d'ailleurs pas spécifié dans l'énoncé.
#10 - 18-02-2015 22:15:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gââteau 94
Je précise un peu la question pour éviter les longues listes 
Quel est le nombre de côtés du gâteau ? S'il y a plusieurs solutions , quelles sont-elles ?
Vasimolo
#11 - 19-02-2015 09:30:45
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
fâteau 94
salut.
pour les polygones équiangles possèdant 4n côtés , les côtés opposés sont parallèles et entiers ; ils diffèrent de a (entier) . en séparant les côtés en 2 groupes et en appliquant la relation de Chasles avec d'une part les côtés de longueur 3,9,7,1,11 & 7 on peut obtenir un triangle équilatéral de côté a . La somme des 6 vecteurs est un vecteur nul .
même opération avec les côtés 6,4,10,8,2 & 12
en règle générale , je me trompe peut-être , ça fonctionnerait pour tous les polygones équiangles possédant 3 x 2^n n>0 côtés comme l'hexagone , le dodécagone , tétraicosagone (24 cotés) ... 48 , 96 .etc...
#12 - 19-02-2015 17:22:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gtâeau 94
Oui ça marche unecoudée mais y'en a d'autres .
Vasimolo
#13 - 20-02-2015 14:04:31
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteauu 94
salut.
toujours avec la relation de Chasles . un décagone avec des angles de 144°
Les côtés opposés sont parallèles et diffèrent de 1 .

#14 - 20-02-2015 14:37:04
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gâetau 94
Avec un gâteau à 6 côtés :
On a vu que équiangle équivaut à ce que la différence entre des côtés opposés soit constante. Evidemment si l'on ajoute le même nombre aux côtés de départ, ça marche encore : par exemple avec les côtés 2,7,4,3,6,5 dans cet ordre. On va donc plutôt chercher une autre solution avec les côtés de 1 à 6.
En raisonnant sur le côté 3, on voit que la différence ne peut valoir que 1, 2, ou 3.
1, c'est l'exemple que tu as donné, 2 ça ne marche pas, 3 ça marche.
#15 - 20-02-2015 18:12:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#16 - 20-02-2015 19:30:28
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteaau 94
Ca marche aussi pour les multiples de 3 par un nombre premier avec eux, je pense...
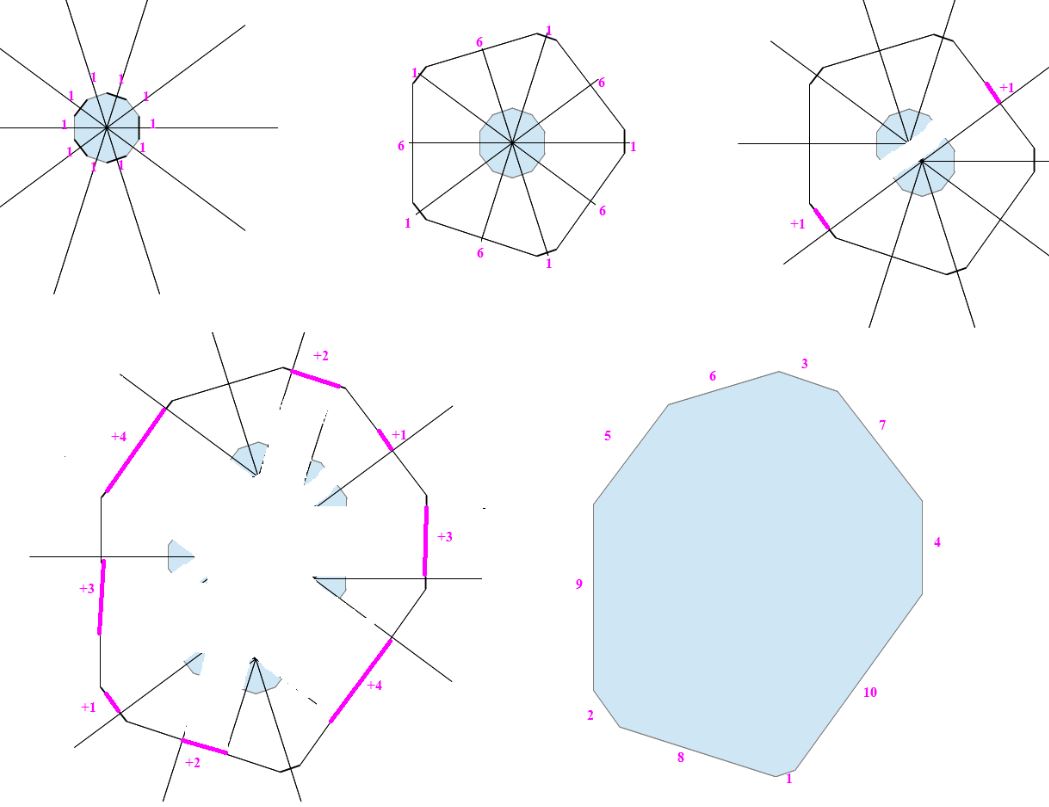
On part du polygone régulier (15 côtés dans ton exemple)
On augmente 1 côté sur 3 (3x5=15) de 0, 5 et 10
Puis 1 côté sur 5 de 0 1 2 3 et 4 :
On peut faire la seconde étape car chaque triangle (prolongé) issu de 3 côtés a des angles de 60° et est donc équilatéral.
Spoiler : [Afficher le message] Pour le fun , je tente : tout produit de 2 premiers entre eux est valable , ainsi que ses multiples. Car on peut faire le même raisonnement avec 5 et 7 ...
Seules les puissances d'un même nombre premier sont impossibles.
#17 - 20-02-2015 19:39:09
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
gâyeau 94
J'ai pas participé à l'énigme (ça me dépasse tout ça) mais quand Vasimolo a proposé le 15, j'ai aussi pensé aux produits de deux nombres premiers. Mais dans ce cas là, on pourrait faire à tétrakaidécagone, ou tétradécagone ou quadridécagone (à 14 côtés quoi  ). ).
#18 - 20-02-2015 19:49:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtteau 94
gwen27 a écrit:Pour le fun, je tente ... seules les puissances d'un même nombre premier sont impossibles.
J'en suis exactement au même point . Je pense avoir prouvé que tout entier qui n'est pas une puissance d'un nombre premier convient . Je n'ai pas encore réfléchi à la réciproque .
Vasimolo
#19 - 20-02-2015 20:31:56
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteaau 94
Ca marche si on admet qu' un polygone à n côtés entier est nécessairement régulier si n est premier.Mais ça reste une conjecture issue du gâteau précédent.
SabanSuresh a écrit:J'ai pas participé à l'énigme (ça me dépasse tout ça) mais quand Vasimolo a proposé le 15, j'ai aussi pensé aux produits de deux nombres premiers. Mais dans ce cas là, on pourrait faire à tétrakaidécagone, ou tétradécagone ou quadridécagone (à 14 côtés quoi  ). ).
Bah oui, tu pars de 14 côtés égaux et entiers. Et tu appliques le même procédé que pour le décagone avec 8 au lieu de 6.
#20 - 20-02-2015 20:34:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
GGâteau 94
@Gwen : n premier => polygone régulier n'est plus une conjecture 
Vasimolo
#21 - 20-02-2015 20:39:31
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteau 49
Dans ce cas, premiers entre eux permet de passer de l'un à l'autre vu que les deux boucles imbriquées 1/n et 1/m donnent la suite de 1 à n x m le tout en restant dans des polygones de base réguliers.
Par contre, pour exclure les puissances pures de nombres premiers, je ne vois pas.
#22 - 20-02-2015 21:19:25
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gâteai 94
Pour un polygone à n côtés, où n = a x b, avec a et b deux nombres premiers entre eux, on fait exactement comme tu as fait pour n=15 côtés, ça marche.
Donc effectivement, si n n'est pas une puissance d'un nombre premier, on peut trouver un polygone équiangle dont les côtés sont n nombres entiers consécutifs.
#23 - 22-02-2015 12:32:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#24 - 22-02-2015 20:18:37
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gâtrau 94
Merci pour ce gâteau Vasimolo, c'était très intéressant !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum