Enigme Logique de Penrose @ Prise2Tete

racine · #1

Petite question logique que je viens de retrouver dans un bouquin de Penrose:

"Si tous les A sont des B et si certains B sont des C, s'ensuit-il nécessairement que certains A sont des C?"

Histoire de mettre un peu la pression, je vous livre le début du paragraphe suivant:

A ce type de question, une majorité d'étudiants a donné la mauvaise réponse. Si les étudiants ordinaires sont à ce point illogiques...

MacArony · #2

La réponse est non bien sûr :

Tous les oiseaux sont des animaux
Certains animaux sont des quadrupèdes

Mais aucun oiseau n'est quadrupède

masab · #3

Non: [latex]A=\{0\},\ B=\{0,1\},\ C=\{1\}[/latex]
Dans cet exemple aucun élément de A n'est dans C.

Franky1103 · #4

Bonjour,
La réponse est NON. En effet, si tous les A sont des B, alors il existe des B qui ne sont pas des A; pour peu que ce soit ces B là qui sont des C, alors aucun A n'est un C.
Bonne journée.
Frank
PS: de quel bouquin de Penrose s'agit-il ?

racine · #5

@Franky1103: il s'agit des ombres de l'esprit

rivas · #6

Il me semble qu'il peut y avoir des B qui ne sont pas des A et que seulement ceux-ci pourraient être aussi des C non? Dans ce cas aucun A n'est un C.

Amusant...

gwen27 · #7

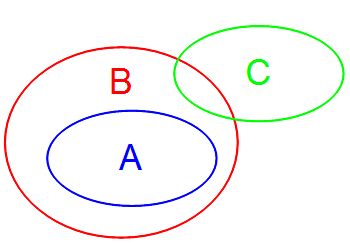
B inclut A et tout ou partie de C Mais A et C peuvent tout de même s'exclure.

racine · #8

Apparemment, il n'y a pas d'étudiants ordinaires qui traînent dans le coin.

scarta · #9

Si tous les hommes sont des êtres vivants, et que certains être vivants sont des chiens, alors y a t'il quelques hommes-chiens ?

Vasimolo · #10

Clairement non avec A={1} , B={1;2} et C={2} .

Vasimolo

nodgim · #11

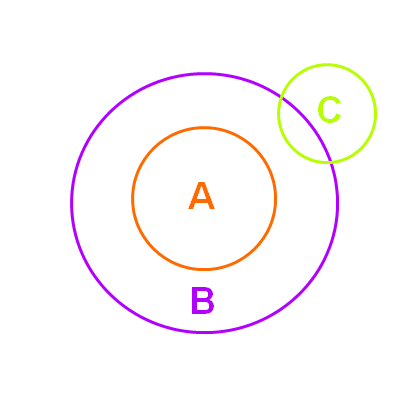
La réponse est non, si on fait un dessin avec des patates, c'est assez évident:
L'ensemble (des) A est inclus dans l'ensemble (des) B, il y a intersection entre l'ensemble B et l'ensemble C, mais rien ne dit qu'il y a forcément intersection entre l'ensemble C et l'ensemble A.

racine · #12

C'est assez amusant de voir la façon de répondre. Ça me semble assez significatif sur le type de logique que chacun met en place.

Jackv · #13

Bien sûr que non : il se peut que tous les B qui sont des C ne soient pas des A, ce qui correspond au cas où l’ensemble B intersecte les ensembles A et C mais où A n'intersecte pas C. (Je sais ce serait encore plus clair avec un petit dessin, mais j'ai la flemme ce soir.)

franck9525 · #14

toutes les bananes sont des fruits, certains fruits sont rouges, ... toutes les bananes restent jaunes malgré tout, vertes à la rigueur.

medihv · #15

Pas sûr de répondre comme il faut mais je tente quand même:

Le piège viendrait à dire que si tous les A sont des B, alors tous les B sont des A (c'est du moins la première pensée que j'ai eu au début). Mais il faut dans ce cas prendre en compte qu'il y a des B qui ne sont pas des A, du coup si certains B sont des C, les B concernés ne sont pas forcément des A. Donc on ne peut pas nécessairement dire que certains A sont des C.

Pas sûr que je viens de sortir la réponse la plus claire du monde

L00ping007 · #16

Une manière de voir les choses : avec des ensembles.

1. "Tous les A sont des B" : [latex]A \subset B[/latex]
2. "Certains B sont des C" : [latex]B \cap C \ne \varnothing[/latex]
3. "Certains Asont des C" : [latex]A \cap C \ne \varnothing[/latex]

Mais avec un petit dessin, on s'aperçoit bien qu'il existe des configurations où on n'a pas 1 et 2 impliquent 3.

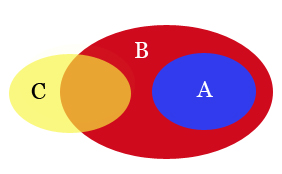
Un contre-exemple :
A : nombres premiers
B : nombres impairs
C : nombres divisibles par 3

Tous les nombres premiers sont des nombres impairs, certains nombres impairs sont divisibles par 3, mais dire que certains nombres premiers sont divisibles par 3 est faux.

scrablor · #17

Évidemment non. Un exemple suffit, essayons qu'il soit simple...

Tous les chats sont des mammifères, certains mammifères sont des chiens... Pourtant aucun chat n'est un chien.

Tous les carrés sont des polygones, certains polygones ont 5 côtés, mais parmi ces derniers on ne trouve aucun carré.

Ah zut, ça en fait deux...

langelotdulac · #18

Bonsoir

Voilà comment je vois l'affaire

Ou :

Donc, non, pas nécessairement

godisdead · #19

"Si tous les A sont des B et si certains B sont des C, s'ensuit-il nécessairement que certains A sont des C?"

A => B
B => C
non, je ne vois pas pourquoi les A seraient des C (mais ce n'est pas impossible non plus)
Tous les B ne sont pas des A, et si ce sont ces B qui sont C ben, y a pas de A qui sont des C !

racine · #20

C'est comme l'école des fans, tout le monde a 10/10.

Tromaril · #21

A est inclus dans B
et l'intersection de B et C est non vide
mais ça ne permet pas de conclure sur celle de A et C : il se peut que A soit un sous ensemble de B-C

donc la réponse est non

Hamdi · #22

Pour moi "certains A sont des C" veut dire qu' "au moins 1 A est C".
Ma réponse est non puisque les B qui sont C et les B qui sont des A peuvent avoir une intersection vide.

halloduda · #23

"certains" signifie "pas forcément tous".
Alors, concluez...

MthS-MlndN · #24

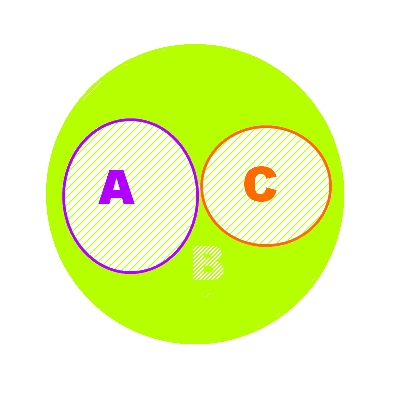
En passant vite dessus, on répondrait oui, mais la réponse est non, et voici un diagramme de Venn pour le prouver par contre-exemple :

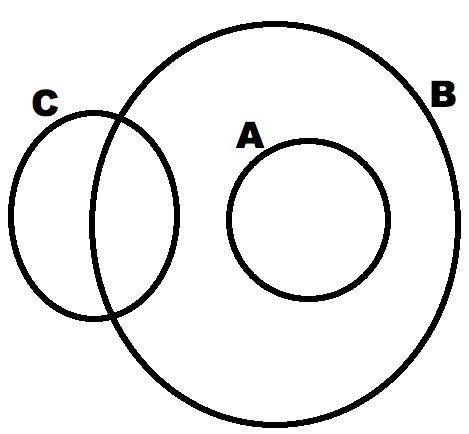
Et la rapide consultation de Wikipedia qui m'a permis de me remémorer les différences entre diagrammes d'Euler, Venn et Carroll, m'a fait atterrir sur cette image, regardez le cas de droite :

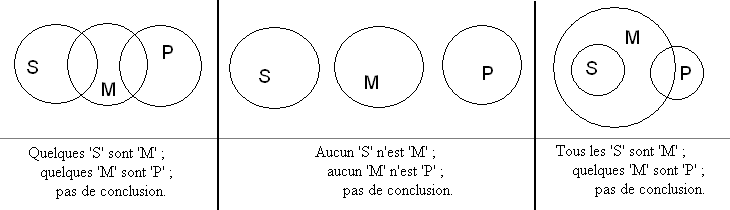
Comme ça, vous croirez que j'ai obtenu la réponse sur Google, et je baisserai dans votre estime (si c'est encore Dieu possible).

Tant pis.

justme · #25

les A égalent Les B et les C à la fois je pense, parce que B et un ensemble des B et des C (pas sûre) :p

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 27-01-2012 14:48:19

Logiqque de Penrose

#0 Pub

#2 - 27-01-2012 15:58:43

Logique d ePenrose

#3 - 27-01-2012 16:20:06

Logique de Pnerose

#4 - 27-01-2012 16:31:22

Loggique de Penrose

#5 - 27-01-2012 16:34:32

logique dz penrose

#6 - 27-01-2012 16:50:59

Logique de Penros

#7 - 27-01-2012 16:57:13

Logique de Penrosee

#8 - 27-01-2012 17:00:36

Logique ed Penrose

#9 - 27-01-2012 17:05:58

logique de prnrose

#10 - 27-01-2012 17:20:11

Loique de Penrose

#11 - 27-01-2012 17:40:05

Loogique de Penrose

#12 - 27-01-2012 18:25:00

Logqiue de Penrose

#13 - 27-01-2012 19:26:14

Logique de Penrosee

#14 - 27-01-2012 19:55:38

Logiqu de Penrose

#15 - 27-01-2012 22:06:40

Logiquee de Penrose

#16 - 27-01-2012 22:45:53

oLgique de Penrose

#17 - 27-01-2012 23:38:10

Logique de Pennrose

#18 - 28-01-2012 00:06:12

logique se penrose

#19 - 28-01-2012 02:03:19

ligique de penrose

#20 - 28-01-2012 03:03:29

logique de peneose

#21 - 28-01-2012 11:02:25

Logiique de Penrose

#22 - 28-01-2012 12:29:45

oLgique de Penrose

#23 - 28-01-2012 17:29:23

Logique dde Penrose

#24 - 28-01-2012 21:57:15

logique de penrise

#25 - 29-01-2012 00:10:21

logiqur de penrose

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums