Enigme Ingénierie géométrique inverse n°1 1/2 @ Prise2Tete

looozer · #1

Bonjour à tous,

Quelle est la propriété remarquable de cette paire de quadrilatères?

La question est très ouverte, je m'en rends compte, mais connaissant les esprits affûtés qui hantent les lieux, je n'en dis pas plus pour l'instant. Je donnerai des indices si nécessaire. Bon amusement

Indice 1 : Spoiler : [Afficher le message]
Indice 2 : Spoiler : [Afficher le message]
Indice 3 : Spoiler : [Afficher le message]
Indice 4 : Spoiler : [Afficher le message]
Indice 5 : Spoiler : [Afficher le message]

azert666 · #2

symetrique opposé inverse

SHTF47 · #3

Ils sont jolis ?

looozer · #4

SHTF47 : Ils sont jolis ?

Bonne réponse, évidemment! Je m'attendais à un coup de ce genre

irmo322 · #5

Ces deux quadrilatères sont tellement quelconques que c'en est remarquable...!

ksavier · #6

Salut,

Doit-on faire la liste de leurs propriétés ?

Ils ne sont pas croisés !
ou encore
Leur intersection est vide, c'est remarquable !

Promath- · #7

Ils ont la même aire????

Juste un indice; Est-ce que il y a un rapport avec les droites remarquables?

Le premier à l'air d'être circonscriptible.
Mais le deuxième non.

racine · #8

Petite question:
les dimensions sont importantes ou seule la configuration compte?

ksavier · #9

ahhhhh la propriété n'est remarquable que pour la paire ...

Et bien je trouve remarquable qu'ils ne soient pas de la même couleur.

autre chose ? définitivement ils ont une intersection vide.

Tiens je viens de remarquer un truc qui se remarque sur ce couple de quadrilatère : l'un est plus grand que l'autre.

Plus sérieusement, j'ai trop peur d'être déçu par une propriété géométrique non raisonnablement accessible. Après tout, il ne doit pas être trop difficile de démontrer que 2 quelconques quadrilatères peuvent être remarquable sous un certain point de vue.

Je m'avoue vaincu et je vais attendre des indices plus consistants.

looozer · #10

Les idées émises jusqu'ici ne vont pas dans la bonne direction.

Courage, j'ai rajouté un indice et j'en promets un plus gros pour demain.

looozer · #11

J'ai rajouté l'indice 3!

titoufred · #12

Ils pavent le plan ?

looozer · #13

titoufred : Il ne s'agit pas d'un pavage du plan.

Franky1103 · #14

J'ai vérifié si les segments formés par les points reliés deux à deux sont concourants: choux blanc.
Puis j'ai vérifié si les segments formés par les milieux de segments reliés deux à deux sont concourants: choux blanc aussi.
J'y retourne, mais pour l'instant, je n'ai rien.
Bonne soirée.

looozer · #15

Franky1103 : Il y a de l'idée

toudoulami · #16

Faut-il utiliser un compas ?

looozer · #17

toudoulami : Bienvenue
On peut utiliser un compas et une latte pour la construction.

victosaurus · #18

Juste pour faire avancer le scmilblick:

Ce pourrait il que ces deux quadrilataires permettent le pavage du plan
comme le pavage de Penrose par exemple?

Promath- · #19

Ils ont les mêmes longueurs de côté?

looozer · #20

victosaurus : Il ne s'agit pas de pavage
Promath- : Ils n'ont pas de côtés de même longueur

looozer · #21

Je rajoute le dernier indice.

looozer · #22

Dans l'espoir d'une bonne réponse, je rajoute du temps et un indice décisif !

ksavier · #23

aie j'ai peur qu'il existe un morphisme continue inversible de [0;1] du premier pentagone (quadrilatère,couleur) vers le second et dont la valeur en 1/2 serait un carré mauve.

looozer · #24

Ta crainte est fondée ksavier
Bien vu!

masab · #25

Effectivement si l'on note
I le milieu de [AM]
J le milieu de [BN]
K le milieu de [CP]
L le milieu de [DQ]
alors le quadrilatère IJKL est un carré... mauve !

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 14-02-2012 21:31:17

ingénierie géométriqur inverse n°1

#0 Pub

#2 - 14-02-2012 22:30:17

ingénierie géométruque inverse n°1

#3 - 14-02-2012 23:00:54

Ingénierie géométrique invers n°1

#4 - 14-02-2012 23:18:41

ingénierie géométrique invzrse n°1

#5 - 15-02-2012 01:00:38

Ingénierie gémoétrique inverse n°1

#6 - 15-02-2012 06:43:09

Ingénierie géométrique niverse n°1

#7 - 15-02-2012 09:43:20

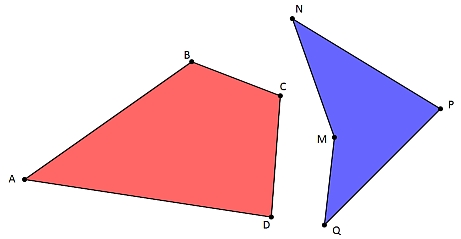
ingénierue géométrique inverse n°1

#8 - 15-02-2012 14:51:37

ingénierie géométrique inveese n°1

#9 - 15-02-2012 18:10:24

ibgénierie géométrique inverse n°1

#10 - 16-02-2012 00:28:39

ingénierie géométrique inversz n°1

#11 - 16-02-2012 16:31:49

Ingénierie géométrique inveres n°1

#12 - 16-02-2012 19:14:43

ingénierie géométrique inverse b°1

#13 - 16-02-2012 20:47:55

Ingénierie géométrique invers n°1

#14 - 16-02-2012 21:51:45

Ingénierie éométrique inverse n°1

#15 - 16-02-2012 22:33:11

ingénierie géométrique invzrse n°1

#16 - 17-02-2012 10:30:18

Ingénierie géométrique inveres n°1

#17 - 17-02-2012 15:39:09

Inénierie géométrique inverse n°1

#18 - 17-02-2012 16:11:06

Ignénierie géométrique inverse n°1

#19 - 17-02-2012 17:21:02

Ingénierie gééométrique inverse n°1

#20 - 17-02-2012 18:59:35

Ingénierie géométrique nverse n°1

#21 - 17-02-2012 19:00:39

ingénirrie géométrique inverse n°1

#22 - 18-02-2012 20:55:52

ingénierie gépmétrique inverse n°1

#23 - 19-02-2012 01:36:10

Ingénierie géométriqe inverse n°1

#24 - 19-02-2012 10:11:34

Inngénierie géométrique inverse n°1

#25 - 19-02-2012 10:57:05

Ingénierie géométrique iinverse n°1

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums