En supposant que la bougie éclaire uniformément dans toutes les directions, qu'on néglige la diffraction de la lumière, que la pièce est d'épaisseur nulle, que le corps de la bougie ne gêne pas (comme le dit le proverbe chinois : "Il fait sombre au pied du phare" :-)), je trouve que la hauteur optimale de la flamme est :

[latex]h=\sqrt{1-r^2}[/latex] où [latex]r[/latex] est le rayon de la pièce de monnaie, soit environ à un mètre de haut si la pièce est petite.

J'y connais rien en éclairage mais je pense qu'il faut que l'angle [latex]a[/latex] soit maximal pour que la pièce reçoive un max de photons...

On a : [latex]a = b^+ - b^-[/latex] et on sait que [latex]\tan b^- = (1-r)/h[/latex] et [latex]\tan b^+ = (1+r)/h[/latex].

Donc: [latex]\tan a = \tan (b^+ - b^-) = (\tan b^+ - \tan b^-)/(1+\tan b^+\tan b^-) = \ldots = 2r/(h + 1 - r^2)[/latex].

En calculant la dérivée par rapport à [latex]h[/latex] et en égalant à [latex]0[/latex], on obtient l'équation : [latex]1-r^2-h^2 = 0[/latex], d'où la solution (qui est bien un maximum et pas un minimum).
Il est justifié de dériver[latex] \tan a[/latex] car elle est croissante sur [latex][0,\pi/2][/latex], intervalle qui nous intéresse, et donc son maximum est le même que celui de [latex]a[/latex].

Ca veut dire quoi éclairer au maximum ?

Si je comprends bien l'enonce je dirais que la quantite de lumiere recut par le piece augmente lorsque la chandelle s'eleve car l'incidence augmente, mais cependant decroit car la distance augmentant l'angle solide diminue.

En schematisant à une projection 2D,

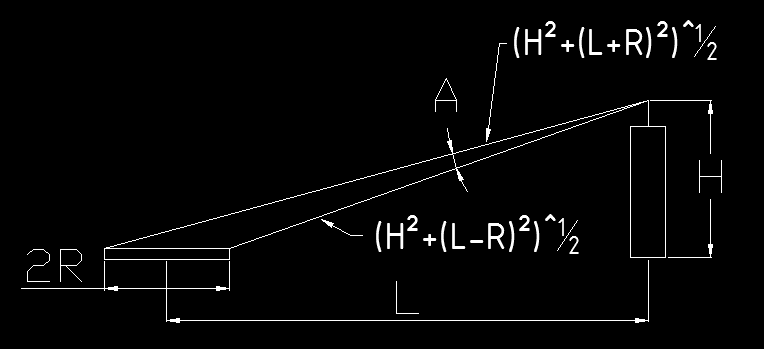
[TeX]A= acos [\frac{~H1^2+H2^2-4R^2}{2H1H2}][/TeX]
H1 et H2 étant les hypoténuses dessinées sur le schéma

soit en dérivant, soit en utilisant Excel (plus rapide), on obtient que l'angle est maximal lorsque H=L. Donc la hauteur donnant le maximal de lumière est lorsque la source de lumière est a 45 degrés, soit une hauteur de 1 mètre lorsque la chandelle est a 1 mètre de la pièce.

Spoiler : [Afficher le message] Les maths, seules, ne vous permettent pas de résoudre cette énigme.

Ouaip, je vois que je ne suis pas le seul à avoir trouvé mon résultat, et en MP Saint-Pierre m'a fourni sa solution qui ne concorde pas. Je continue à me demander en quoi je me trompe... la brillance de la source lumineuse n'influe normalement en rien sur la proportion de lumière reçue, en revanche celle-ci est directement liée à l'angle sous lequel la bougie "voit" la pièce et qui doit être le plus grand possible.

Passer à un angle solide ne devrait pas changer le résultat car la surface projetée de la pièce sur la sphère englobant la bougie sera maximal quand l'angle en 2D est maximal.

Ouinnnn je veux qu'on m'esplik

On est obligé de supposer que la densité de photons émise par la bougie est homogène dans toutes les directions (aucune information n'est fournie si ce n'est pas le cas). Il faut aussi supposer qu'éclairage maximal veut dire "plus grand nombre de photons reçus".
Donc l'angle sous lequel la flamme "voit" la pièce doit être le plus grand possible si l'on veut que celle-ci reçoive le plus de photons possibles.

Avec les notations de franck l'angle qui est la différence des angles des hypothénuses avec la verticale vaut:
[TeX]\alpha(H)=arctan(\dfrac{H}{L+R})-arctan(\dfrac{H}{L-R})[/TeX][TeX]\alpha'(H)=\dfrac1{L+R}.\dfrac1{1+\dfrac{H^2}{(L+R)^2}}-\dfrac1{L-R}.\dfrac1{1+\dfrac{H^2}{(L-R)^2}}=\dfrac{L+R}{(L+R)^2+H^2}-\dfrac{L-R}{(L-R)^2+H^2}[/TeX][TeX]\alpha'(H)=0 \Leftrightarrow H^2(L+R-(L-R))=(L-R)(L+R)^2-(L+R)(L-R)^2[/TeX]
Ce qui se simplifie en (je vous passe les détails): [latex]H^2=L^2-R^2[/latex]

Et si on néglige le rayon de la pièce par rapport à la distance entre la bougie et la pièce (sans doute la partie non mathématique de la démonstration à laquelle SaintPierre fait référence), on trouve en effet que H=L: la flamme de la bougie doit être à 1m de haut...

Sans faire de calcul, il me semble qu'il faut prendre en compte le fait que l'intensité lumineuse se distribue sur la surface d'une sphère.
Pour une intensité I initiale sur une surface nulle (on suppose la source ponctuelle), elle sera de I/(4PiR²) à une distance R de la source.

gasole a écrit:

Eh bin Rivas, tu ne m'as pas lu (je suis vexé), car tu trouves comme moi... sauf que moi, je ne dérive pas l'angle mais sa tangente. Mais d'après SaintPierre en MP, la hauteur optimale est 0, 71, se serait-il trompé ?

Ben si je t'ai lu. Et d'ailleurs j'ai bien noté que je trouvais comme toi.
J'ai rédigé ma solution justement pour ça.
Je n'avais pas de MP et je ne savais pas par ailleurs qu'il trouvait 0.71 (sans doute V2/2) mais je ne comprends pas en la situation d'où vient cette valeur.

@racine: Comme je l'ai indiqué dans mon post précédent, sans info supplémentaire, on ne sait pas quoi calculer (angle solide, ...). Mais je doute fort que le résultat en soit changé radicalement. Si on veut utiliser l'angle solide, il faut calculer l'angle solide de la pièce vu depuis la flamme (en négligeant l'absence de courbure de la piece) et faire une règle de 3 entre I, 4pi.L^2 (L distance entre la flamme et la pièce) et l'angle solide de la pièce. L'angle solide global est 4.pi. L'angle solide de la pièce n'est pas simple à calculer, intersection d'un cylindre penché avec une sphère... Je vais rester à mon approximation en 2D...

La flamme etant une source ponctuelle elle 'voit' la piece au travers d'un angle solide.
Le flux lumineux emis est réparti sur 4pi.
Un element de surface de la piece (dP) est vu au travers d'un angle solide dA.
En photometrie on a dans ce cas:

dA = dP cos(b) / D^2

ou b est l'angle formé par la normale à dA et la normale à dP ( qui est parallele à la bougie ici).
D est la distance flamme - piece soit D = (1 + h^2)^1/2 avec h = hauteur de la bougie et 1^2 la distance a la bougie (1m donné).

cos(b) = h / D donc

dA = dP h / D^3 = dP h /(1 + h^2)^3/2

l'eclairement (E) maximum est obtenu quand dA / dP est max;
E = Flux_lumineux_emis / 4pi x dA/dP

On recherhe donc max(dA / dP) = max( h /(1 + h^2)^3/2) = max(1/(h^-2/3 + h^4/3)^3/2) = min(h^-2/3 + h^4/3).
dérivée = 0 ==> H = 1/rac(2)= 0.71

@racine : manquait le cos(b)

naddj a écrit:

En me relisant, je crois surtout que je devrais accepter l'idée que les mathématiques sont loin, très loin derrière moi.

Je me fais aussi souvent cette réflexion !

M***e ! C'est la crise...

Je vais revendre mon casque

Une fois qu'on accepte de travailler en 3D, ce n'est plus vraiment de la physique, on doit bien pouvoir les retrouver ces formules, "il n'y qu'à" maximiser l'angle solide... :-)