 |
#1 - 15-02-2012 10:43:46
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Une boule dans nu tétraèdre
Maintenant qu'il est clos, je vous propose (verbatim) un des problèmes des éliminatoires du 26è championnat que j'ai trouvé très "esthétique" (ne me demandez pas ce que ça veut dire pour moi pour un problème de maths  ). ).
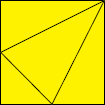
Dans un carré de côté 2012 mm, on a tracé le patron de tétraèdre représenté ci-dessous, où le sommet situé en haut à droite est relié aux milieux de
deux côtés.
On veut réaliser le tétraèdre et y enfermer une boule qui soit parfaitement tangente aux quatre faces du tétraèdre.
Quel sera le diamètre de cette boule ?
On prendra, si besoin est 1,414 pour [latex] \sqrt2[/latex], 1,732 pour [latex]\sqrt3[/latex] et 3,1416 pour [latex]\pi[/latex] et on donnera la réponse arrondie au millimètre le plus proche.
PS: La case réponse valide la réponse numérique sans unité. Je serai en vacances lors de l'expiration du délai mais je suis certain que certains donneront une solution très détaillée qui tiendra lieu de solution officielle en mon absence. Je vérifierai à mon retour 
#2 - 15-02-2012 13:39:31
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Une booule dans un tétraèdre
Javais commencé a ecrire quelques équations et utilisé Wolfram pour les résoudre, mais j'ai du faire une erreur, puisque Wolfram me donnait une solution complexe.
Sur ce, j'ai abondonné avec wolfram, et l'ai refait a la main.
Voici ce que j'ai fait:
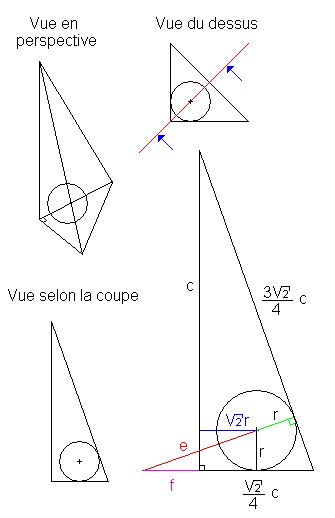
Je coupe le tetrahedre en 2 parties égales en suivant la mediatrice du triangle principal (la ligne rouge de la vue du dessus. Et on regarde cette coupe en suivant les 2 fleches bleues.
Pour simplifier, au lieu de calculer r (le rayon) en fonction de c (le coté du carré), on suppose r=1, et on calcule c en fionction de r (en ignorant temporairement la valeur reelle de c qui est de 2012):
En remarque que (a cause de l'angle droit ou la sphere est tangente a l'hypothenuse du grand triangle) l'angle entre e et f est le meme que l'angle en haut du triangle. On pose donc l'équation suivante:
(f + √2/4 c) / (e+1) = 3√2/4 qui peut s'ecrire (f + √2/4 c) = 3√2/4e + 3√2/4
On remarque aussi que en bas a droite du triangle, la distance du coin du triangle au 2 points de contact est la meme, on pose donc l'équation suivante:
(f + √2/4 c) = 3*(√2/4 c-√2) qui peut s'ecrire (f + √2/4 c) = 3√2/4c - 3√2
d'ou :3√2/4e + 3√2/4 = 3√2/4c - 3√2 qui peut s'ecrire 3√2/4(c-e) = 3√2(1+1/4) ou encore : c-e = 4*(1+1/4) ou encore e=c-5
On a également l'équation:
e/(f+√2) = (3√2)/4
et comme e=c-5, on re-ecrit: 4*(c-5) = 3√2f+3√2√2 ou encore 4c-20 = 3√2f+6 ou encore 4c -3√2f-26 = 0
le 2eme equation ci dessus peut se reecrire:
f-√2/2c+3√2=0 que l'on multiple par -√2 : c -√2f - 6 =0
on multiple encore par 4: 4c - 4√2f - 24 = 0
on soustrait 4c -3√2f-26 = 0, ce qui nous donne -√2f+2 =0 puis f = √2.
on remplace f dans cette équation: e/(f+√2) = (3√2)/4
et ca nous donne : e/(2√2) = 3√2/4 ou encore e = 3
comme e=c-5, c=8
Ceci, bien sur avec r=1.
Comme en fait c=2012, on en deduit r=2012/8 ou encore D (le diametre) = 2012/4 = 503.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#3 - 15-02-2012 14:16:52
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
une noule dans un tétraèdre
Bizarre : « la réponse arrondie au millimètre le plus proche » et « avec une virgule décimale si nécessaire » me semblent contradictoires si la réponse est en millimètres.
J'avais trouvé 503 mm pour le diamètre, mais j'ai dû cafouiller quelque part, je reviendrai avec des idées plus claires dès que possible...
Celui qui fuit les casse-tête ne vaut pas un clou.
#4 - 15-02-2012 14:29:42
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Une boule dans un tétrèdre
J'ai corrigé la case réponse. J'avais rippé d'une case sur mon clavier.
La réponse n'est pas complexe (la valeur de la réponse en tout cas  ). ).
#5 - 15-02-2012 14:55:52
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
Une boule dans un tétaèdre
Merci pour la correction !
Le tétraèdre sera trirectangle. Si on place l'origine au sommet où les trois angles droits se rejoignent, on peut avoir les trois autres sommets en A (a,0,0), B (0,a,0) et C (0,0,2a) où a=1006. La plan (ABC) a donc pour équation 2x+2y+z=2a. Le centre I de la boule - équidistant des 3 plans du repère - est de coordonnées (r,r,r) où r désigne le rayon de la boule.
Une formule classique donne la distance de I au plan (ABC) : il faut que celle-ci soit égale au rayon r.
| 2r+2r+r-2a | / sqrt(2²+2²+1²) = r
| 5r-2a | = 3r
Deux solutions :
* r=a qui donne une boule tangente à l'extérieur du tétraèdre ;
* r=a/4 qui donvient et donne 2r=a/2.
Le diamètre 2r vaut donc 503 mm.
[edit] : J'avais confondu 1006 et 2012 dans ma démo 
Celui qui fuit les casse-tête ne vaut pas un clou.
#6 - 15-02-2012 15:34:44
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
une boule dans un tétrzèdre
503, maintenant que je connais la réponse.
Au début, j'avais trouvé 499,33...
Un promath- actif dans un forum actif
#7 - 15-02-2012 17:44:38
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Une boule dans un tétraère
Bonjour,
Le tétraèdre a un coin "doublement droit". Si je fais deux coupes suivant les diagonales, je vois que le cercle est inscrit dans deux triangles isocèles de côtés respectifs: a/2; a/2; aV2/2 et a; av2/4; 3aV2/4.
Le diamètre de la boule (ou du cercle) vaut le quadruple du rapport de la surface du triangle sur son périmètre. Dans les deux cas, je trouve D=a(1-V2/2)
AN: (comme à l'école) a=2012mm donne D=589mm
Bonne journée à tous.
Edit: La case réponse ne valide pas ma solution: j'ai dû faire une erreur quelquepart (je rectifierai plus tard)
#8 - 15-02-2012 18:21:07
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Une boule dan sun tétraèdre
Diamètre = 2r = 503 mm = 2012/4
On exprime de deux façons le volume du tétraèdre, dont on connaît l'aire.
L'une est [latex]V = \frac {rS} 3 \,, avec S=2012^2[/latex].
Pas besoin de [latex]\pi, \sqrt 2, \sqrt 3[/latex].
Complément pour rivas
On peut calculer le volume du tétraèdre :
- soit en calculant la hauteur, puis [latex]V = \frac {hS_0} 3 = \frac{hS} 8[/latex]
([latex]S_0[/latex] = aire de la base).
- soit par le déterminant de Cayley-Menger ou la formule de Piero della Francesca,
qui en est dérivée.
NB Ces formules sont au tétraèdre ce qu'est la formule de Héron au triangle.
- ou plus simplement, le tétraèdre étant trirectangle, son volume est [latex]\frac {1* \frac 1 2*\frac12*2012^3}6[/latex]
#9 - 15-02-2012 18:24:47
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Une boule dans un tétaèdre
Bonne réponse de scrablor. Sa démonstration demanderait quelques compléments de preuve pour pouvoir servir de correction mais elle est bonne (et c'est la même que la mienne par ailleurs).
Promath, la démonstration est plus intéressante que le résultat 
Franky, ce n'est pas la bonne réponse et il est difficile de voir où la démo présente un problème car sa rédaction est difficile à lire 
halloduda a la bonne réponse et apparemment une démonstration différente et intéressante. Peux-tu la détailler un peu pour le plaisir des lecteurs?
#10 - 15-02-2012 19:05:48
- betelgeuse
- Habitué de Prise2Tete
- Enigmes résolues : 34
- Messages : 14
Une boule dans n tétraèdre
Le rayon de la boule inscrite est donné par la formule 3V/S où V est le volume du tétraèdre et S l'aire totale des faces du tétraèdre.
Le tétraèdre a 3 faces qui sont des triangles rectangles donc il s'agit d'un tétraèdre trirectangle. La base est le triangle rectangle isocèle de dimensions 1006 ; 1006 et 1006√2 et sa hauteur est 2012.
V = (1006 x 1006 /2) x 2012/3 et S = 2012 x 2012
On en déduit facilement le rayon de la boule (251,5 mm) puis le diamètre.
Ignorant la formule de départ, j'avais d'abord fait les calculs en créant un repère en 3 dimensions basé sur les arêtes perpendiculaires du tétraèdre et en utilisant la formule de calcul de distance dans un tel repère entre un point et un plan.
#11 - 16-02-2012 00:05:37
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
une boule dans un rétraèdre
Rebonjour,
J'ai compris mon erreur dûe à une vision 3D eronnée du problème.
Le tétraèdre est doublement droit (c'est un cube tronqué).
Je fais une coupe longitudinale dans le plan de symétrie du tétraèdre.
J'obtiens un triangle rectangle de côtés a; aV2/4 et 3aV2/4
J'ai nommé a le côté du carré de départ et r le rayon de la sphère.
Je prends l'angle droit comme origine de mon repère orthonormé.
Le cercle a pour équation: (x-r)²+(y-rV2)²=r²
L'hypothénuse a pour équation: y=(a-x)V2/4
Je cherche le point d'intersection du cercle et de l'hypothénuse: ce qui me donne une équation du second degré qui est: (9/8)x²-x(r+a/4)+2(r-a/4)²=0
Le cercle est tangent à l'hypothénuse: le discriminant de cette équation est donc nul, ce qui me donne: (r+a/4)²-9(r-a/4)²=0 simplifié en: (4r-a/2)(2r-a)=0
Je rejette la solution r=a/2 pas crédible et il me reste donc r=a/8 soit d=a/4
AN: d=503mm validé par la case-réponse.
Bonne soirée.
PS: Je n'ai pas traité cette modification sous forme d'édit pour plus de lisibilité.
#12 - 17-02-2012 10:20:53
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Ue boule dans un tétraèdre
Bonne réponse de betelgeuse qui utilise aussi la méthode du volume comme halloduda qui a précisé les formules utilisées (merci pour les références).
dhrm77 a illustré et complété sa bonne réponse par une démonstration différente (peut-être un peu compliquée?). Wolfram est devenu de nos jours ce qu'était la calculatrice scientifique il y a 20 ans: un outil à utiliser avec précaution et modération. Rien ne remplace une bonne feuille de papier et un crayon pour raisonner 
Bonne réponse aussi de Franky avec une astuce intéressante (le discrimant nul pour l'intersection lorsqu'il y a tangence).
Pas besoin en effet des différentes valeurs approchées, elles sont souvent données pour ne pas donner d'indice sur le simplicité de la solution.
#13 - 17-02-2012 11:21:05
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Une boule adns un tétraèdre
Presque sans trigonométrie 

#14 - 17-02-2012 16:24:22
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Une boule dans un tétraèder
Allez, j'essaie !
On a un tétraèdre rectangle. Je suppose pour simplifier les calculs que le carré du patron fait 2 de côté (je multiplierai à la fin la longueur par 1006), et je construis un repère orthonormal direct à partir du coin de tétraèdre cubique. Cela me donne comme coordonnées pour chacun de mes points du tétraèdre :
O(0;0;0);
A(1;0;0);
B(0;1;0);
C(0;0;2)
L'équation des 4 plans des faces sont :
(OAB) : z=0
(OAC) : y=0
(OBC) : x=0
(ABC) : 2x+2y+z-2=0
Soit S le centre de la sphère : S(a,b,c) et le rayon R.
le centre S de la sphère doit se trouver à une distance R des plans (OAB), (OAC) et (OBC), donc a=R, b=R et c=R et donc S(R,R,R)
Enfin, la sphère doit se trouver à une distance R du plan incliné (ABC), donc :
|2R+2R+R-2|/racine(2²+2²+1²)=R
|5R-2|/3=R
(5R-2)/3=R ou (2-5R)/3=R
5R-3R=2 ou 2=8R
R=1 impossible car le centre est alors à l'extérieur du tétraèdre
ou R=1/4
et donc le diamètre sera 1/2
Avec un carré de côté 2012mm, je multiplie toutes les distances par 1006, le diamètre de ma sphère sera donc 503mm.
#15 - 17-02-2012 22:44:09
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
une voule dans un tétraèdre
Bonne réponse de gwen27 avec de belles illustrations et une méthode encore différente. C'est toujours intéressant de voir toutes les méthodes différentes d'attaquer et de résoudre un même problème.
golgot59 trouve lui aussi le bon résultat avec la même approche que celle que j'avais utilisée.
Je vais être Offline une semaine maintenant. Je viendrai voir les derniers posts lors de mon retour. A bientôt.
#16 - 18-02-2012 00:35:41
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Une boule dans nu tétraèdre
Merci pour l'idée d'utiliser le volume, ça m'a permis d'abandonner mon idée d'utiliser des coordonnées barycentriques, je pense que je ne m'en serais pas sorti.
Je passe sur l'existence et l'unicité d'une sphère tangente aux 4 côtés, il doit exister de telles preuves sur le Net. Intuitivement, on peut s'en convaincre en enlevant la base du tétraèdre, en le retournant (comme un cornet de frites en fait). Si on met une boule à l'intérieur, elle arrive à se caler au fond du cornet. Et en augmentant progressivement le diamètre de la boule, celle-ci va bien finir par être tangente au plan de la face que l'on a enlevée.
J'appelle r le rayon de la sphère, et O son centre. En choisissant 4 points parmi les 5 (les 4 sommets + le point O), on définit un autre tétraèdre. On peut alors définir 4 tétraèdres, disjoints, dont la réunion est le tétraèdre initial. Et les hauteurs de ces 4 nouveaux sont à chaque fois la distance R (distance de O aux faces)
Le volume d'un tétraèdre peut s'exprimer à l'aide d'une de ses hauteurs h et de l'aire A de la face correspondante :
[TeX]V = \frac{Sh}3[/TeX]
Ainsi, le volume V du tétraèdre initial peut s'écrire ainsi, en fonction des aires A, B, C, D de ses 4 faces :
[TeX]V = \frac{Ar}3 + \frac{Br}3 + \frac{Cr}3 + \frac{Dr}3[/TeX]
Mais ô magie, la sommes des 4 aires A, B, C, et D vaut l'aire du carré de départ ! Donc :
[TeX]r = \frac{3V}{a^2}[/TeX]
Il ne reste donc plus qu'à calculer le volume du tétraèdre.
En remarquant qu'une des arêtes (le côté du carré) est orthogonale à l'une des faces (le petit triangle rectangle isocèle), on a :
Le triangle a une aire qui vaut [latex]\frac{a^2}8[/latex], et :
[TeX]V = \frac13\frac{a^2}8a[/TeX]
Après simplification, on trouve :
[TeX]r = \frac a8[/TeX]
Dans notre cas, a=2012, et comme on veut le diamètre[latex]\fbox{d = 503}[/latex]
Qui aurait pu croire que la valeur était aussi simple 
#17 - 18-02-2012 10:35:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Une boule dans un tétaèdre
J'ai trouvé une méthode très rapide , je doute qu'on puisse faire plus court .
Je prend un carré de côté 4 mm ( il suffit de multiplier les longueurs par 503 pour revenir au modèle initial .
Le volume V de la pyramide : 3V=8
les quatre faces ont pour aires 4 , 4 , 2 et 6 .
La grande pyramide est constituée de quatre petites pyramides dont la base est l'une de ses faces et la hauteur est "r" le rayon du cercle inscrit . Si on ajoute le volume de ces quatre pyramides on obtient 3V=16r donc r=0,5 et d=1 .
Le diamètre est 503 mm .
Vasimolo
Edit : en fait il n'y a même pas besoin de calculer chacune des aires il suffit de remarquer que leur somme est égale à 16 mm² et le tour est joué .
#18 - 18-02-2012 17:43:04
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Une buole dans un tétraèdre
halloduda a écrit:Ces formules sont au tétraèdre ce qu'est la formule de Héron au triangle.
et
betelgeuse a écrit:Le rayon de la boule inscrite est donné par la formule 3V/S où V est le volume du tétraèdre et S l'aire totale des faces du tétraèdre.
Je ne connaissais pas cette formule toujours utile de connaître: on en apprend tous les jours sur ce site. 
Vasimolo a écrit:La grande pyramide est constituée de quatre petites pyramides dont la base est l'une de ses faces et la hauteur est "r" le rayon du cercle inscrit. Si on ajoute le volume de ces quatre pyramides on obtient 3V=16r.
C'est une méthode courte, simple, efficace: je suis impressionné. 
#19 - 18-02-2012 18:43:05
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
une boule sans un tétraèdre
Moi je trouve que la réponse de L00ping007 est admirable.
Par contre celle de Vasimolo qui est sans doute (sous entendu le sens premier qui "sans aucun doute") la plus courte je n'ai pas compris pourquoi partir d'un carré de 16mm² ? Cela revient au même que celle de L00ping007 non ? 
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#20 - 18-02-2012 18:59:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Une boule adns un tétraèdre
Oui Looping a utilisé la même méthode que moi et sa rédaction est bien plus claire 
J'avais modifié la taille du carré pour simplifier les calculs car j'ai pris la mauvaise habitude de calculer "à la main" . En fait après mon PS , le seul calcul effectif résiduel est celui de l'aire du carré initial et la réduction perd beaucoup de son intérêt .
En tout cas un joli petit problème avec une belle solution .
Vasimolo
#21 - 18-02-2012 19:07:04
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Une boue dans un tétraèdre
Merci 
Les mauvaises habitudes c'est de se servir de sa calculatrice, en contrôle que je l'ai où non ma note ne change pas alors autant ne pas s'en servir on perd moins de temps.
Par contre pour simplifier les calculs je préfère ta méthode faut-il encore voir que 2012 est divisible par 503 xD ce qui n'est pas mon cas.
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#22 - 18-02-2012 19:26:31
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Une boule danns un tétraèdre
#23 - 19-02-2012 20:15:36
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
une boule danq un tétraèdre
Mille excuses à LOOping007 pour avoir involontairement ignoré sa solution, identique effectivement, avec plus de détails, à celle de Vasimolo.
Il y a ceux qui ont vu cette astuce sur la décomposition des volumes et il y a ceux qui ne l’ont pas vu (comme moi  ) et qui ont dû se faire des calculs plus compliqués dans un repère. ) et qui ont dû se faire des calculs plus compliqués dans un repère.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







