Je pense que oui.

Si le canard se place au centre et part dans une direction diamétralement opposée à celle du chat, ce dernier va devoir faire un choix : vers la droite ou la gauche ?

Et à un moment donné de ce parcours, le chat et le canard seront alignés sur un autre diamètre . Seulement le canard sera alors bien plus près du bord, il lui suffira de bifurquer.


Et pour la clarté : (elle doit encore être limite même si je me comprends )


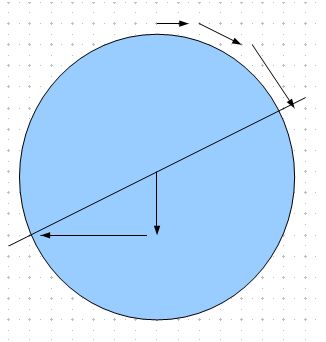
Dans le cas limite, la canard peut pousser ce jeu en suivant un début de spirale tout en restant à l'opposé du chat jusqu'à parcourir un cercle à 1/4 du rayon.
Il lui reste 3/4 du chemin à parcourir, dans un rapport 1/4 or  3 < pi


Sans tomber sur le plus rapide : Le canard parcours un tout petit peu moins du quart du rayon et tourne "en rond" jusqu'à se retrouver à l'opposé du chat qui peine à suivre. Puis il file vers le bord opposé au chat qui peut toujours courir.

Je connais déjà cette énigme ici:http://www.samuelboudet.com/fr/enigmes/niki.php (une belle sélection d'énigme par ailleurs)

Une solution simple:
  Quand le canard est dans un cercle de rayon 1/4 du rayon de l'étang, sa vitesse angulaire est plus rapide que celle du chat, il peut donc s'éloigner lentement du centre jusqu'à la limite du cercle de rayon 1/4 en veillant à ce que le chat reste opposé à lui par rapport au centre de l'étang.

  Dès qu'il sort du petit cercle, le chat le gagne en vitesse angulaire. Suivant qu'il parte sur la droite ou la gauche, le canard par du coté opposé jusqu'au bord tangentiellement au petit cercle.
le calcul :
1) pour le canard d=V(1-1/4²) < 0.97
2) pour le chat d'=pi+Arcos(1/4) > 4.45
4d<d' donc le canard s'est bien échappé

PS : si le chat change de sens, c'est à son désavantage, il suffit alors au canard d'aller droit au bord le plus proche. Dès que le chat change de sens de nouveau  le canard reprend  la stratégie tangente avec encore moins de chemin à parcourir. Sinon, si le chat passe le l'autre côté, le canard prend la tangente dans l'autre sens avec idem une avance encore plus grande.

Amusant, et bien plus compliqué qu'il n'y paraît !

Il faut remarquer que le canard peut nager et faire un tour complet à la vitesse du chat à condition de parcourir un cercle de diamètre 4 fois plus petit que l'étang.

En se déplaçant sur un cercle très légèrement inférieur à ce petit cercle, le canard va pouvoir aller plus vite que le chat et donc finir par se trouver sur ce cercle "diamétralement" opposé au chat.

Une fois en cette position, il restera au canard à faire une distance de 3/4 du rayon R de l'étang pour atteindre le bord, alors que le chat devra faire un demi-tour d'étang, soit Pi x R. Comme il va 4 fois plus vite que le canard, en supposant que le canard va à une vitesse V, il mettra un temps de Pi.R/(4V), alors que le canard atteindra le bord après 3R/(4V).

Comme 3<Pi, le canard parviendra à goûter l'herbe !

Marrante cette énigme, encore une fois il fallait poser les bonnes conditions (j'étais parti au début sur une spirale très galère !)

Probablement oui, ma réponse n'est pas mathématique mais si le canard va vers le chat jusqu'au point où ce dernier ne peut pas l'attraper puis il fait semblant de longer le diamètre, il fait quelques mouvements de nage (sans trop avancer) et le chat va se dépêcher de courir au point où le canard fait semblant d'aller. Puis il ne reste plus qu'au canard de rebrousser rapidement le chemin et comme ça le chat ne pourra l'attraper.
Voilà, c'est pas mathématique mais j'essaierai de faire une démonstration quand j'en aurai le temps.

Zut alors, je la connais celle là....

Oui effectivement, il suffit au canard d'aller droit au bord quand il est opposé au chat à 1/4 du centre car 3/4*4<pi

En fait j'ai donné une solution compliqué qui correspond à l'énigme à laquelle j'avais déjà réfléchi (dans le lien) : le poursuivant cours 4.5 fois plus vite au lieu de 4, ça augmente un peut la difficulté.

Le canard va se poster à une distance [latex]r/4-\epsilon[/latex] du centre de l'étang ([latex]\epsilon[/latex] tout petit),
Le chat se place bien sûr au plus près face à lui.
Le canard commence à effectuer des cercles sur ce rayon. Le chat qui essaie de le suivre va se retrouver en retard de [latex]4 *n*\epsilon[/latex] au bout de n tours.
Quand le décalage correspond à un demi-tour le canard fonce vers la rive la plus proche dont il se trouve à [latex]3*r/4 + \epsilon[/latex]. Le chat a lui [latex]\pi*r[/latex] à parcourir.
Le canard arrivera avant lui au bord de l'étang si [latex]\epsilon < (\pi-3)*r/4[/latex].
Il faudra qu'il fasse très vite pour manger et surtout qu'il ait toujours des yeux derrière la tête quand il effectue ses circonvolutions !

Logiquement, le point d'équilibre (et donc de départ pour le canard) se situe au milieu de l'étang car le chat cherche à minimiser sa distance au canard, ensuite le canard part à l'opposé de la direction actuelle du chat, soit [latex]r[/latex] à traverser en ligne droite, or le chat à exactement [latex]\pi r[/latex] à franchir, or [latex]\pi\leq 4[/latex] donc le canard ferait mieux de rester au milieu de son étang.

EDIT: en fait le canard fera le tour de l'étang plus vite que le chat tant qu'il sera sur un cercle de rayon [latex]d\leq\frac{ r}{4}[/latex]
car s'il avance à [latex]v[/latex] il fait un tour en [latex]\frac{2\pi d}{v}[/latex] et le chat en [latex]\frac{2\pi d}{4v}[/latex], d'où [latex]\frac{2\pi d}{v}\leq [latex]\frac{2\pi r}{4v}[/latex][/latex] ce qui donne [latex]d\leq\frac{ r}{4}[/latex] donc le canard peut s'approcher infiniment près du cercle de rayon [latex]d_{max} = \frac{ r}{4}[/latex] en ayant le chat à l'endroit de son choix (diamétralement opposé donc si possible ^^)
ce qui fait une distance de [latex]\frac{ 3r}{4}[/latex] contre [latex]\pi r[/latex] toujours pour le chat.
Le canard ne peut avoir de meilleure possition de départ (à moins d'une condition initiale particulière).
donc le canard peut profiter de l'herbe mais dans le cas d'une vitesse supérieure de [latex]\frac{4\pi}{3}[/latex], il ne pourra plus

EDIT2: en fait c'est même plus simple, je n'avais pensé que rien n'empêchait le canard de nager autrement qu'en ligne droite.

@AlexF & dhrm77 : oui bravo !

@Vicuel : Oui bravo.

Je vous laisse admirer la solution simple et limpide proposée par golgot.