Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 31-08-2013 20:24:11
fâteau 62Bonsoir à tous
#0 Pub#2 - 01-09-2013 10:47:01
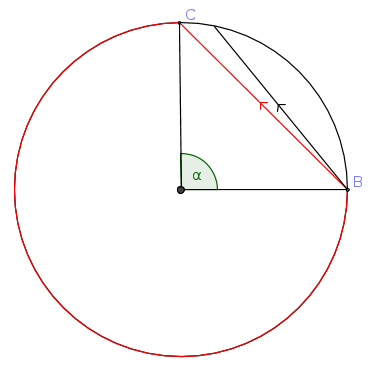
Gâtea u62Est ce un hasard si tu as dessiné ce qui semble être la longueur max, c'est à dire un carré ? #3 - 01-09-2013 11:34:59#4 - 01-09-2013 12:42:50
gâteai 62@Nodgim : je ne connais pas la réponse et tu as peut-être raison , mais le dernier coup de couteau va quand même forcément "casser" un peu la symétrie . #5 - 01-09-2013 22:46:33
Gâteua 62Bonsoir, Il y a sûrement plus simple. #6 - 02-09-2013 13:24:12
Gâteauu 62Très bon boulot Cogito Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.