|
#1 - 01-09-2016 19:24:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 02-09-2016 00:21:59
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâteau 26
Le PS c'est pour te décharger des propos de tout hurluberlu ? 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#3 - 02-09-2016 00:26:42
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâtaeu 126
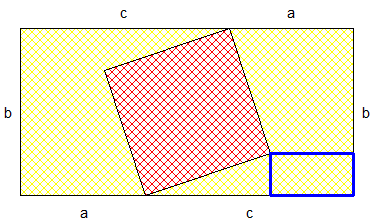
En étudiant la figure, on trouve que les côtés du rectangle bleu mesurent (a+c-b)/2 et (a+b-c)/2.
Comme l'aire du rectangle bleu vaut 6, cela donne a²-(c-b)²=24, puis en utilisant que a²+b²=c², il vient que b(c-b)=12.
12 n'ayant que 6 diviseurs, seules 6 valeurs sont possibles pour b, et parmi elles, une seule correspond à un triplet pythagoricien : si b=12, alors c=13 et a=5 (il est facile de vérifier que c'est bien une solution au problème), et c'est l'unique solution possible.
#4 - 02-09-2016 06:57:57
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
gâtzau 126
Bonjour,
a=5, b=12, c=13
Triangle bleu 3x2
#5 - 02-09-2016 12:08:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 12
@Shadock : oui 
@Ebichu : parfait .
@Enigmatus : oui , est-ce la seule solution ?
Vasimolo
#6 - 02-09-2016 12:18:58
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteua 126
Soit k le côté du carré, k1 et k2 < k1 ses projections (verticale et horizontale).
On a: k² = k1² + k2², avec: b = k1 + k2 et: c – k1 = a – k2
Ce qui donne: k1 = (-a + b + c) / 2; k2 = (a + b – c) / 2 et: k = V[c.(c – a)]
Par ailleurs: a + b + c = 6a donne: a = (b + c) / 5
De plus: k2.(c – k1) = 6 donne: (a + b – c).(a – b + c) = 24 ou: c = 12/b + b
Donc b ne peut valoir que: 1; 2; 3; 4; 6 ou 12. Etudions chaque cas.
Les cinq premiers donnent des valeurs non naturelles. Il reste:
a = 5; b = 12; c = 13 (solution unique)
#7 - 02-09-2016 18:43:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtaeu 126
C'est bon Franky .
Vasimolo
#8 - 03-09-2016 08:17:33
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâeau 126
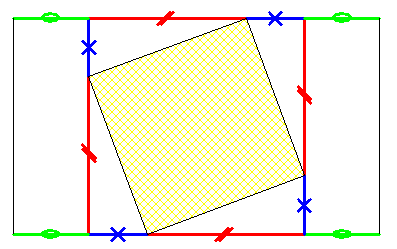
Vu que la diagonale du carré forme un losange avec les deux sommets du grand rectangle, ses sommets et ceux des rectangles sont alignés.
Conclusion : les deux rectangles sont homothétiques. La surface du grand est donc de 36 x 6 = 216
Le seul triplet pythagoricien qui permet d'obtenir ce résultat est 5 12 13
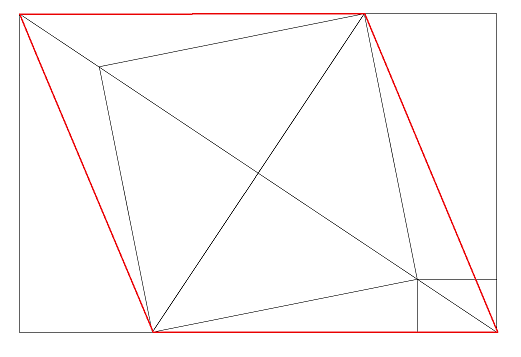
Reste quand même à vérifier la taille du petit rectangle :
La diagonale du grand : rac(468) = 6 rac(13)
La diagonale du carré : rac(208) = 4 rac(13)
C'est OK.
#9 - 03-09-2016 18:10:43
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gâteaau 126
Bonjour,
Si on note AB les deux extrémité de la diagonale du carré touchant le grand rectangle (B en haut, A en bas) et C le coin inférieur droit, on a:
[TeX]tan(\alpha) = tan(\widehat{BAC}) = \dfrac{b}{c-a}[/TeX]
Le triangle ABC étant isocèle en C, on a
[TeX]\widehat{BCA} = \pi - 2\alpha[/TeX]
Si on note [latex]\beta[/latex] l'angle de la diagonale du rectangle bleu, on a:
[TeX]\beta =\dfrac{\widehat{BCA}}{2} = \frac{\pi}{2} - \alpha [/TeX]
(car la diagonale du rectangle bleu est portée par la bissectrice de [latex]\widehat{BCA}[/latex] )
Enfin, avec x et y les côtés du triangle bleu (x hauteur, y longueur) , on obtient [latex]tan(\beta) = \dfrac{x}{y} = \dfrac{1}{tan(\alpha)} =\dfrac{c-a}{b} [/latex]
En utilisant [latex]xy = 6[/latex], on a [latex]y^2 = 6\dfrac{b}{c-a}[/latex] et [latex]x^2 = 6\dfrac{c-a}{b}[/latex]
Ensuite, en utilisant [latex]a+b+c = 6(x+y)[/latex] je n'arrive pas à obtenir quelque chose de simple à cause des radicaux, je dois être fatigué...
Edit:
J'ai quand même trouvé le couple évident: 5,12,13 avec x et y égaux à 2 et 3 et je pense que je suis pas loin de la démonstration...
Edit2:
En fait, je suis vraiment nul! 
[TeX](x + y )^2 = 6(\dfrac{b}{c-a}+\dfrac{c-a}{b}) + 12[/TeX]
J'arrive donc après simplification à [latex]6^3(b+c-a)^2 = b(c-a)(a+b+c)^2[/latex]
Or on a [latex](b+c-a)^2 < (a+b+c)^2[/latex]
On en déduit que pour trouver une solution, il faut [latex]b(c-a)<6^3[/latex]
Il suffit donc de vérifier pour les premiers triplets qu'il n'y a pas d'autres solution...
(Après vérification à la main, j'en déduis que c'est très peu probable)
Edit3:
Effectivement, il y avait des inversions, je modifie tout ça!
C'était fantastique comme énigme, merci beaucoup!
#10 - 03-09-2016 19:55:34
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
#11 - 04-09-2016 09:16:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
fâteau 126
@Gwen : très bien et plutôt expéditif .
@Caduk : la réponse est bonne mais j'ai du mal à suivre tes calculs , il doit y avoir des inversions de lettres .
@Halloduda : est-ce l'unique solution ?
Vasimolo
#12 - 04-09-2016 11:13:49
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#13 - 04-09-2016 11:36:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtea 126
@Nobodydy : tu te prives du meilleur 
@Gwen : ta solution était complète : on n'impose pas que les côtés du petit rectangle soient entiers ( ce qui ajoute d'ailleurs une difficulté au problème ) .
Vasimolo
PS : je n'aime pas laisser traîner trop longtemps les problèmes "en aveugle" mais si quelqu'un veut un peu de temps avant de découvrir les brillantes solutions déjà fournies ...
#14 - 04-09-2016 12:18:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteau 1266
Si, car rien ne prouvait que la diagonale du carré fasse 2/3 de celle du rectangle.
Je prouvais juste de manière simple que, s'il y avait une solution, cela ne pouvait être que 5 12 13. Là, je suis sûr du rapport 1/6.
#15 - 04-09-2016 12:44:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 126
Tu connais l'aire du grand rectangle et celui du petit , le rapport est immédiat , non ?
Vasimolo
#16 - 04-09-2016 12:49:13
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteau 12
Non, je dis que le grand rectangle est homothétique avec le petit et donc , si le petit fait 6, le grand fait 216. La réciproque n'est pas vraie.
Si tu avais posé le problème avec 24 cm^2 et 3 fois la taille, mon raisonnement aurait été le même. Vérifier est indispensable, sauf si le fait que l'énoncé affirme l'existence d'une solution suffit. Il faut vérifier que le carré en est un et donc que ses diagonales ont la même longueur. L'alignement des sommets n'utilise que les propriété d'un losange, pas d'un carré.
#17 - 04-09-2016 13:53:40
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gâteau 26
Un peu plus efficace, on a:
[TeX]\dfrac{6}{b(c−a)}=(\dfrac{a+b+c}{6(b+c−a)})^2[/TeX]
En utilisant la caractérisation des triplets pythagoriciens:
[TeX]a=p^2-q^2\; ,\; b=2pq\; ,\; c = p^2+q^2[/TeX]
On a alors:
[TeX]\dfrac{6}{4p^3q}=(\dfrac{2q(p+q)}{12p(q+p)})^2 \iff \dfrac{6}{pq}=(\dfrac{2q}{6})^2 > \dfrac{q^2}{9}[/TeX]
On a également [latex] (\dfrac{2p(a+b+c)}{6(b+c-a)})^2 > \dfrac{p^2}{9}[/latex]
On déduit que [latex]pq = 6n^2[/latex]
Si [latex]n\geq3[/latex] alors [latex]\dfrac{6}{pq} \leq \dfrac{1}{9} \leq \dfrac{p^2}{9} < (\dfrac{2p(a+b+c)}{6(b+c−a)})^2[/latex]
si [latex]n = 2[/latex], p ou q est supérieur à 3 donc [latex]\dfrac{p^2}{9} > \dfrac{1}{4}[/latex] ou [latex]\dfrac{q^2}{9} > \dfrac{1}{4}[/latex] donc il n'y a pas de solutions
donc [latex]n=1[/latex]
On obtient alors [latex]pq = 6[/latex] d'où on en déduit les couples (5,12,13) et (12,35, 37).
Seul le premier satisfait les conditions, et on retrouve bien (x,y) = (2,3)
#18 - 04-09-2016 17:39:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#19 - 04-09-2016 18:48:37
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
#20 - 04-09-2016 19:18:54
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteeau 126
@Vasimolo: Veux tu dire qu'à cause de diverses considérations géométriques, le petit et le grand rectangles sont homothétiques ? Et, comme le rapport des périmètres est 6, celui des surfaces est forcément 6²=36.
#21 - 04-09-2016 19:26:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtzau 126
@Franky : oui 
J'ajoute un peu de temps et s'il n'y a rien de neuf ce soir je lève le masque .
Vasimolo
#22 - 04-09-2016 19:45:49
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteau 12
Je vois bien le dessin. Il est évident en le voyant que ma solution fonctionne .
Ce que je te redis, c'est qu'avec ma méthode sans formule ni calcul (ou presque) , je ne tiens pas compte de la contrainte "carré" Ton dessin le tient pour acquis.
Si :
Il veut en plus que l'aire du rectangle bleu soit de 6 cm² et que le périmètre du gâteau soit six fois celui de ce même rectangle .
devenait :
Il veut en plus que l'aire du rectangle bleu soit de 24 cm² et que le périmètre du gâteau soit trois fois celui de ce même rectangle .
J'obtiendrais ça
Vu que la diagonale du carré forme un losange avec les deux sommets du grand rectangle, ses sommets et ceux des rectangles sont alignés. (en utilisant le fait qu'un carré soit un losange et qu'il est formé par la jonction de 2 triangles isoccèles)
Conclusion : les deux rectangles sont homothétiques. La surface du grand est donc de 9 x 24 = 216
Le seul triplet pythagoricien qui permet d'obtenir ce résultat est 5 12 13
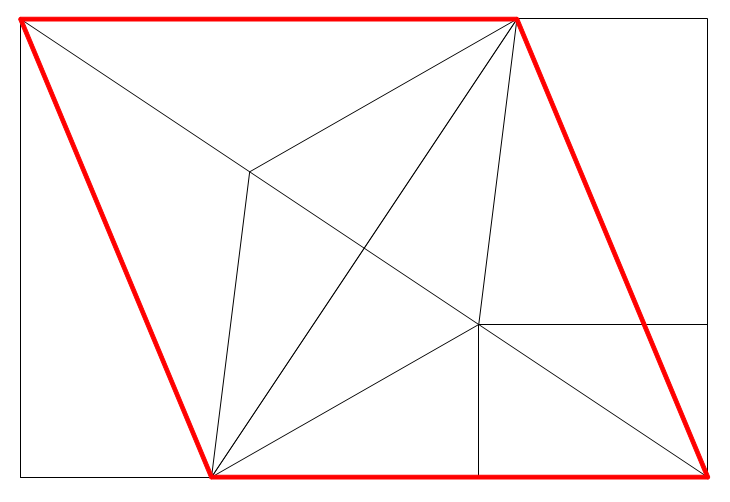
(on verrait vite que ce n'est pas valable, et donc qu'il n'y a pas de solution )
Mais avec 6,1cm^2 et 5,80 fois le périmètre il faudrait avoir un compas dans l'oeil pour dire que la solution est fausse et que l'on n'a pas un carré central.
Donc si une solution existe, on prouve en 3 coup de cuillère à pot que c'est 5 12 13 mais il faut le vérifier (même rapidement) .
#23 - 04-09-2016 23:02:49
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteau 1126
On est d'accord. La solution supposée unique est triviale et la vérification aussi, je disais juste qu'elle était nécessaire, pour la forme.
#24 - 05-09-2016 19:14:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtau 126
J'avais une solution à la Ebichu que je trouve très élégante mais j'ai adoré celle de Gwen : la géométrie c'est magique 
Bien sûr merci à tous les autres .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum