 |
#1 - 17-01-2014 19:45:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 19-01-2014 00:40:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 6
Une petite précision pour répondre aux MPs et à ceux qui se posent peut-être la même question : le dessin est juste une illustration naïve du problème 
La question est uniquement dans le texte .
Un bon point de départ : chercher la forme que peut bien avoir le gâteau de mon insupportable pâtissier en oubliant ses histoires de triangles ( dans un premier temps ).
Bon courage à ceux qui cherchent 
Vasimolo
#3 - 19-01-2014 08:47:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
gâtrau 67
Le pâtissier a peut être fait un escalier: 4 marches et 4 contre marches composées chacune de 2 rectangles identiques collés. On aura du mal à faire une découpe en 15 rectangles, mais aucun à en faire une en 16 triangles.
#4 - 19-01-2014 09:51:25
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâeau 67
Pour un rectangle, il y a 4 angle droits.
Pour chaque rectangle ajouté, celui-ci ne doit pas être entièrement contenu dans la surface des précédent car il ne serait pas obligatoire. Il ne peut pas non plus prolonger cette surface. Il doit donc "déborder" sur un côté créant une sorte de forme en escalier ce qui rajoute 2 angles de 90° à son pourtour, soit 180°.
Au final, 16 rectangles nécessiteront 360° + 15x180° Même si chaque triangle occupe une place entre trois sommets du polygone, il manquera 180° soit un triangle. On ne peut pas y arriver à moins de 17 triangles.
En gros : chaque triangle peut occuper au maximum un angle droit et proéminant mais le premier rectangle en amène plusieurs.

#5 - 19-01-2014 11:46:31
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
gâteai 67
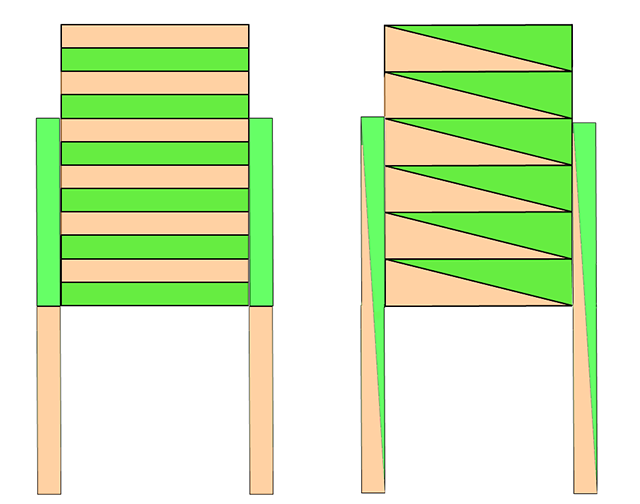
Voici une solution qui ressemble plus à un panneau d'information qu'à un gâteau.
Ma conviction de la non divisibilité en 15 rectangles est plutôt intuitive pour l'instant mais j'essaierai de la mettre en forme.
#6 - 19-01-2014 12:11:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#7 - 19-01-2014 12:21:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteauu 67
Je ne dis pas qu'il n' y a pas d'autres polygones dans ce cas, mais pour répondre à la question initiale: non, ce n'est pas de l'intox, on peut faire un gâteau sécable en 16 rectangles ou triangles, mais non en 15 rectangles.
Moi aussi, vu le dessin, je pensais implicitement à des parts identiques (en surface tout au moins).
Peux tu reformuler ta question ?
#8 - 19-01-2014 12:24:04
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteau 6
C'est Vasimolo, j'avais oublié que tu manges des plus grosses parts que moi ;-)
Du coup mon gâteau s'écrase 
#9 - 19-01-2014 12:27:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea 67
@Nodgim : il suffit de lire la question sans regarder le dessin 
J'ai illustré pour rendre l'énigme plus attrayante , j'aurais pu ( dû ) m'en passer mais un gâteau sans image ...
Désolé 
Vasimolo
#10 - 19-01-2014 12:27:50
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteau 76
Ca ne change rien. Pour 5 rectangles tu as toujours 5*2 +2 sommets.
(comme pour 16 : 32+2 )
Soit au minimum 12x90° à remplir avec les angles de 5 triangles ce qui est impossible.
#11 - 19-01-2014 12:37:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteauu 67
@Gwen : ce que je ne comprends pas dans ton argumentation , c'est que tu dis qu'un triangle ne peut pas récupérer plus de 180° sauf s'il touche un sommet "rentrant" du gâteau mais que ce n'est pas bien grave car ça ne change rien à l'affaire . Il peut aussi en toucher plusieurs , c'est sûrement aussi sans conséquence , tout ça ce sont des affirmations , pas une argumentation 
Ou alors je n'ai rien compris 
Vasimolo
#12 - 19-01-2014 13:14:05
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâetau 67
Au lieu de passer par les angles, passons par les côtés.
Ton gâteau a au moins 12 côtés distincts, s'il n'en avait que 10, on pourrait le paver avec 5 rectangles.
Un triangle ne peut en suivre que 2 vu qu'ils sont tous à angle droit les uns avec les autres.
#13 - 19-01-2014 13:20:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâetau 67
A la question posée, il me semble bien avoir répondu entièrement, non ?
#14 - 19-01-2014 17:47:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 6
@Gwen : ce n'est pas si simple même s'il y a un lien entre le nombre de côtés et le nombre maximal de rectangles , tu avais trouvé le bon angle d'attaque avec ton premier argument il manquait juste un petit quelque chose .
@Nodgim : tu as complètement répondu au problème mais ta réponse n'est pas la bonne .
Vasimolo
#15 - 19-01-2014 17:58:00
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Gâteau 6
Je construis un gâteau avec n parts de dimensions L=2*l. Je les positionne en escalier et je découpe le tout par un seul segment qui passe alternativement par un coin et le milieu d'une longueur de chaque part. Pour n rectangles, j'ai (n+1) triangles. Je ne vois pas comment faire n triangles.
#16 - 19-01-2014 18:03:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
fâteau 67
Pour compléter ma réponse à Gwen : un gâteau à 2n+2 côtés peut être recouvert par n rectangles mais possiblement par moins et quelle conséquence sur le nombre de triangles ????
Vasimolo
#17 - 19-01-2014 19:56:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
fâteau 67
Euh... au minimum n+3 angles droits sortants ?
#18 - 20-01-2014 06:45:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 76
Si ma réponse n'est pas bonne, c'est que tu peux découper l'escalier en 15 rectangles. J'attends de voir.
#19 - 20-01-2014 13:20:54
- tirom
- Amateur de Prise2Tete
- Enigmes résolues : 17
- Messages : 4
Gâteau 76
Sile gâteau est rond, on peut le couper en trois parts redivisées en cinq.
#20 - 20-01-2014 14:44:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 677
Bon , j'ai enfin pris un peu de temps pour lire tout ça 
@Gwen : c'est bon . En fait tu avais tout dit dès le début mais je n'avais pas compris comment tu traitais le cas des angles "rentrants" .
@Nodgim : je pense que tu ne réponds pas à la bonne question mais sans illustration j'ai du mal à voir où tu te perds .
Vasimolo
#21 - 20-01-2014 21:20:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâeau 67
Une petite explication pour compléter celles de Gwen :
Les angles du gâteaux font tous 90° ou 270° . Un tel gâteau avec n angles de 270° a n+4 angles de 90° pour 2n+4 angles en tout . On démontre aisément par récurrence que pour empêcher le découpage du gâteau en n rectangle , il faut au moins n angles rentrants . Le gâteau qui nous intéresse a donc au moins 15 angles rentrants pour un total d’au moins 34 angles . Les angles des triangles doivent recouvrir au moins 90° dans chaque angle du gâteau il faut donc au moins 34×90180=17 triangles pour couvrir le gâteau .
Merci à tous les participants et à Gwen en particulier pour sa solution .
Vasimolo
#22 - 20-01-2014 22:00:52
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
âteau 67
Vasimolo a écrit:Bon , j'ai enfin pris un peu de temps pour lire tout ça 
@Gwen : c'est bon . En fait je n'avais pas compris comment tu traitais le cas des angles "rentrants" .
Vasimolo
Je ne les traitais pas, je les négligeais comme des facteurs aggravants. On peut imaginer des situations complexes mais elles ne font que reporter le problème. Un angle interne de plus = 180° = 1 triangle en plus. La solution la moins coûteuse est en escalier ou similaires.
#23 - 21-01-2014 18:38:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
gâyeau 67
Bonsoir Vasimolo,
Je comprends pourquoi tu n'as pas compris ce que j'avais écrit, compte tenu du message de Gwen juste avant, qui pouvait faire penser que je construisais la même chose que lui.
En fait, je construis un escalier à 4 marches et 4 contre marches. Au lieu d'escalier, j'aurais pu dire un gâteau linéaire en zig zag. C'est un polynome, donc conforme à l'énoncé de départ. Il y a donc 8 segments, on peut les couper chacun en 2 pour former 16 rectangles ou 16 triangles, mais sûrement pas 15 rectangles.
Est ce plus clair ?
#24 - 21-01-2014 19:14:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gââteau 67
@Gwen : aggravant d'accord mais les "rentrants" sont indispensables à l'interdiction d'une découpe en 15 rectangles . Un triangle peut "absorber" bien plus que 180° des angles du gâteau en frôlant les sommets rentrants et pour cette raison il faut prendre quelques précautions 
@Nodgim : je te jure que je ne le fais pas exprès mais je ne comprends toujours pas ce que tu veux dire . Une bonne âme pour m'expliquer ?
Vasimolo
#25 - 21-01-2014 19:44:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 677
Ne jure pas Vasimolo, je te crois sur parole.
En fait, j'ai complètement erré sur le sujet: bien sûr qu'avec 8 segments, on peut tracer 15 rectangles, on peut même en tracer de 8 à l'infini. J'en étais sans doute resté depuis le début à des parts identiques...
On oublie mes sottes interventions sur le sujet.
|
 |

 Accueil
Accueil
 Forum
Forum









