Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#26 - 05-04-2014 16:01:57#0 Pub#27 - 05-04-2014 23:04:08
Gââteau 74@Nolina : le triangle est acutangle ( 3 angles aigus ) . #28 - 06-04-2014 09:53:23
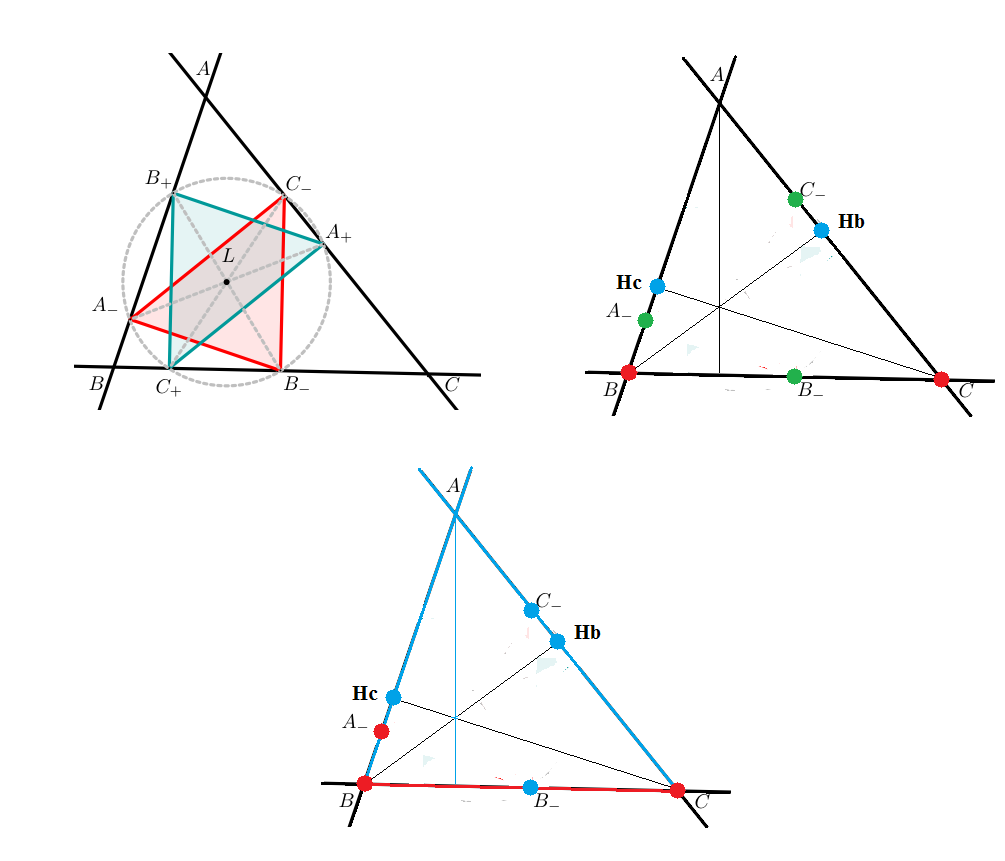
Gâteau 4Avec le point de Lemoine du triangle, on construit un des deux triangles auto projetants : #29 - 06-04-2014 10:01:38
Gâteu 74Si l'on inscrit un rectangle R dans le triangle T (1 coté C de R colinéaire avec 1 coté de T) alors un coté de R adjacent à C ne peut avoir les 2 sommets de même couleur. Sinon, avec 2 pts rouges sur un de ces cotés, l'autre coté doit forcément avoir 2 bleus, sinon on pourrait immédiatement tracer un triangle rectangle. Mais dans ce cas, on aurait un coté à 2 pts rouges et un coté à 2 pts bleus, tous les 2 adjacents à C, et dans ce cas avec un pt quelconque bleu ou rouge sur C, on peut dessiner un triangle rectangle. #30 - 06-04-2014 10:35:57#31 - 06-04-2014 18:58:04
Gâteaau 74Le principe est bien de prouver que deux sommets de même couleur autorisent une hauteur de couleur opposée ou il y a plus simple ? #32 - 06-04-2014 19:05:41#33 - 06-04-2014 19:07:18
fâteau 74Je donne ma solution qui ressemble beaucoup à celles de Gwen et Nodgim . #34 - 06-04-2014 19:52:03#35 - 06-04-2014 19:58:45
Gtâeau 74Vasimolo, le triangle bleu exterieur pourrait avoir ses cotés parallèles au triangle vert intérieur, ce serait plus lisible. C'est un peu comme ça que j'ai construit le triangle intérieur, mais bon la justification de son existence suffit. #36 - 06-04-2014 23:24:42#37 - 12-04-2014 18:17:23
Gâteau 744Bonjour à tous! #38 - 12-04-2014 18:29:58
gâtezu 74Bienvenu sur Prise2Tête, Tetris ! #39 - 12-04-2014 19:04:53
fâteau 74@Tetris : tu es sans doute resté coincé sur la première page , il y a pas mal de développements du problème sur la deuxième Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.