Hello,
Voici mes conclusions personnelles:



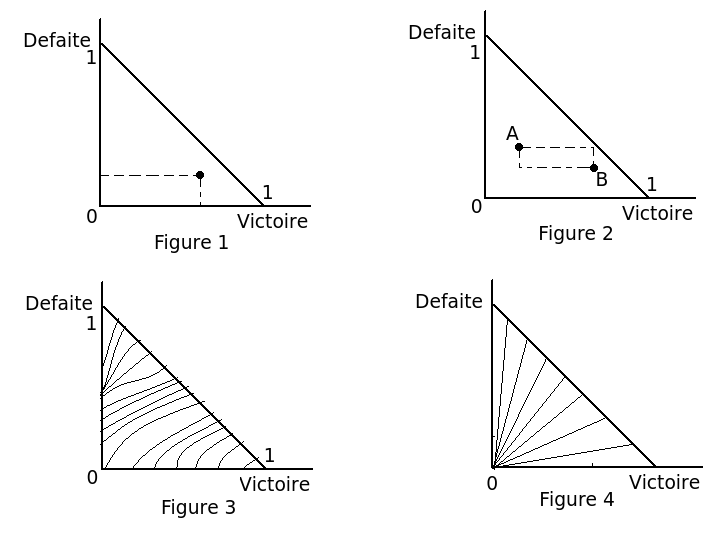
Ce qu'on aimerait expliciter c'est un ordre, pas nécessairement stricte, sur l'ensemble des statistiques possibles. Ci-dessus une illustration de cet ensemble, à un point de ce triangle correspond une statistiques (au point de la figure 1 correspond en gros (V=65%,E=15%,D=20%))

Invariant rationnel: ce qu'on aimerait c'est assurer que lorsque deux stats sont les coins haut gauche et bas droite d'un rectangle (figure 2), que la stratégie bas droite soit toujours considérée comme la meilleure. C'est simplement l’interprétation géométrique d'une statistique dominée par une autre (A défaite égale plus de victoires, à victoire égale moins de défaites ou plus de victoires et moins de défaites).

Après le reste est très subjectif il y a plein de manières légitimes de vouloir ordonner ces statistiques. On peut couvrir une large famille de relations d'ordre sur le triangle en imaginant une structure en strates/nervures (figure 3). Il suffit que chaque nervure soit une fonction croissante, et qu'on considère les stats sur les nervures en bas et/ou à droite comme meilleures et on a une relation d'ordre qui respecte l'invariant rationnel. Ce que vous avez proposé fait partie de cette famille.

Lorsqu'on considère un processus de classement en attribuant des récompenses ou des malus à la victoire à la défaite à l’égalité en fait on se trouve dans un cas particulier de la famille ci dessus ou les strates sont des droites parallèles. Avec les deux protocoles extrêmes strates verticales et strates horizontales. On sent bien implicitement que ne considérer que les victoires comme importantes n'est pas si générique et intuitif, penser au cas (V=29% E=71% D=0%) et (V=30% E=0% D=70%) . Je pense qu'entre deux telles stats la majorité des gens préfère celle qui pourtant gagne le moins souvent. Un exemple extrême juste pour montrer la limite du modèle.

Il y a d'autres manières d'ordonner nos stats: par exemple si on considère comme strates toutes les droites passant par l'origine (figure 4). Ça s’interprète facilement; c'est la proportion de victoire sur l'ensemble des non-nuls. Par exemple une équipe (V=30% E=60% D=10%) pourra sembler préférable à certains à équipe (V=40% E=30% D=30%) parce que cette première gagne 3 fois plus qu'elle ne perd. Une des limites de cette méthode c'est qu'une équipe du type (V=5% E=94% D=1%) est une très bonne équipe ce qui illustre le fait que cette méthode de classement ne pénalise pas l'anti-jeu.

Personnellement je pense que mon intuition irait vers des strates correspondant à un scoring agressif pour les valeurs faibles (pour pénaliser l'anti-jeu) mais une approche proportionnelle (paragraphe précédent) pour les valeurs fortes. Avec au sein d'une même strates les "meilleurs" considéré comme vers la droite.

On peut aussi remettre en cause le fait de ne considérer que des relations d'ordre. Car ce qu'implicitement dans notre tête on réalise c'est plutôt un processus d’élection: parmi un ensemble fini de stats on est capable de sélectionner celle qui nous parait la meilleure sans pour autant s'encombrer de devoir classer tout l'espace de stats possible. Ce qui peut donner lieu à pas mal de paradoxe sur le choix ou des équipes peuvent être classées différemment en fonction de la population dans laquelle on les inscrit pour les comparer, bref ce n'est plus une relation d’ordre mais ça n'en est pas moins un procédé rationnel.