|
#1 - 14-02-2015 11:01:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 14-02-2015 12:11:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteu 93
sin (18°) étant un "multiple" rationnel de rac(5) --> 1/4 (rac(5)-1)difficile de l'obtenir comme rapport des deux côtés avec deux nombres entiers.
#3 - 14-02-2015 12:12:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâtea u93
En fait, tu demandes si le sinus de Pi/10 est rationnel ?
Je dirais que non, pourtant celui de Pi/6 l'est....
#4 - 14-02-2015 12:30:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 9
Joli tir groupé de Gwen et Nodgim 
Si vous voulez vous occuper pour le week-end : il m'a montré aussi un heptagone avec les mêmes contraintes 
Vasimolo
#5 - 14-02-2015 19:47:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 39
Pour répondre aux MP
Bien sûr le pentagone régulier à côtés entiers convient mais ce n'est visiblement pas le gâteau présenté par le pâtissier .
J'ajoute que s'il y a deux bonnes réponses , les justifications laissent quelques abysses à combler .
Vasimolo
#6 - 15-02-2015 10:49:57
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteau 9

Soit le pentagone régulier de côté a ... e et b sont donc entiers
je prolonge en traçant des paralellogrammes (trais bleus),
on en déduit que c est entier aussi.
Puis on trace un trapèze régulier (côtés rouges) et on voit que c étant entier , d doit l'être.
Un simple calcul sur les angles montre que le triangle construit est isocèle (et de côtés entiers)
Donc 2d cos (36°) = e
e/2d est rationnel, pas cos (36°)
Ca ne marche que d=e=0 soit pour un pentagone régulier.
PS on peut aussi construire le second trapèze pour se convaincre que b=0
#7 - 15-02-2015 11:16:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 39
C'est bon Gwen , bravo !!!
On peut faire un peu plus simple en prolongeant les côtés b , c et e 
Vasimolo
#8 - 15-02-2015 11:16:53
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteu 93
salut.
un pentagone équiangle possède 5 angles de 108° .
si je pars d'un pentagone régulier ABCDE avec 5 côtés entiers et que je translate le côté AB de façon à conserver les 5 angles .
je dois diminuer les côtés BC et DA d'une quantité entière n . Alors il est impossible pour le côté AB de rester entier pour la raison suivante:
appelons z le nombre d'or . z = (V5 + 1)/2 est irrationnel.
et sin18° = m/n = (z-1)/2 est irrationnel et si n est entier alors m est irrationnel . le côté AB mesure après translation AB + 2m non entier.
#9 - 15-02-2015 11:46:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteu 93
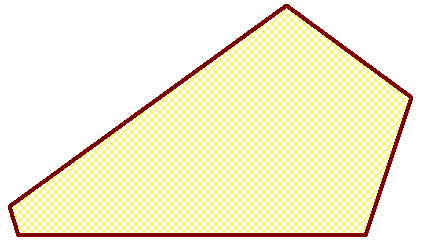
Ta réponse est juste Unecoudée mais la justification n'est pas correcte . On peut par exemple construire un gâteau équiangle non régulier à dix côtés entiers et pourtant les sinus des angles ne sont pas rationnels .
Vasimolo
#10 - 15-02-2015 12:22:24
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
GGâteau 93
salut vasimolo .
mais je m'en suis tenu uniquement au gâteau que ton pâtissier t'a montré .
c'est à dire un pentagone . je n'ai pas attaqué les autres polygones .
#11 - 15-02-2015 12:26:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtzau 93
Oui Unecoudée , mais l'argument de ta démonstration s'applique à l'identique pour un décagone , non ?
Vasimolo
#12 - 15-02-2015 15:21:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâtzau 93
En fait toute figure dont le nombre de côté n'est pas premier le permet.
Pour les autres, je ne sais pas même si j'ai l'intuition que c'est impossible.
#13 - 15-02-2015 17:36:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 93
Ton intuition est bonne Gwen et il y a une démonstration pas trop difficile . Pour le cas ou le nombre de côtés n'est pas premier il y a une petite variante assez amusante qui fera l'objet d'un prochain gâteau 
Vasimolo
#14 - 16-02-2015 09:59:41
- maahlaha
- Amateur de Prise2Tete
- Enigmes résolues : 20
- Messages : 1
fâteau 93
les angles sont de 108 degres
#15 - 16-02-2015 18:53:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâetau 93
J'ajoute un petit indice pour ceux qui pataugent dans le nougat 
Ne cherchez pas trop compliqué .
Vasimolo
PS : je rappelle que cos(72°) n'est pas rationnel .
#16 - 16-02-2015 21:20:15
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
gâteay 93
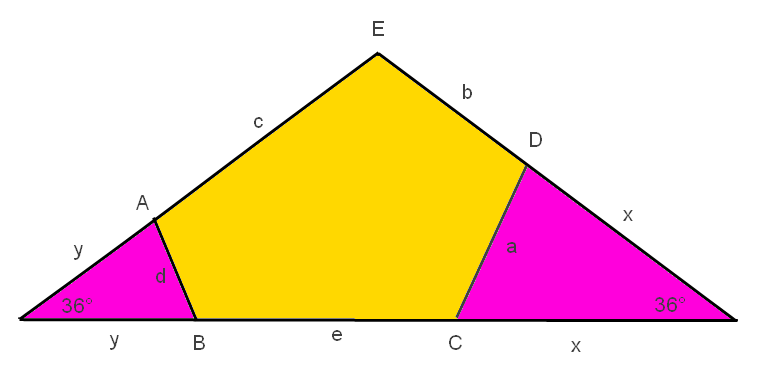
Aaarrrggghhh !
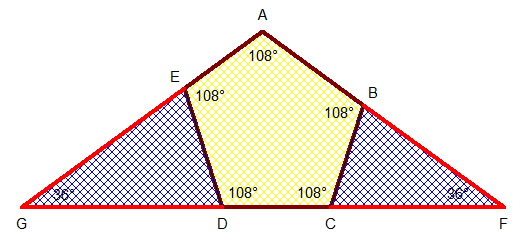
Lors d'une réunion ennuyante ce matin, j'avais justement pensé à prolonger les côtés du pentagone pour former un triangle. Et là, ça devient plus facile !
On a les relations: x = a / (2.sin18°), et: y = d / (2.sin18°)
De plus: c + y = b + x, ce qui donne: 2.sin18° = (a - d) / (c - b)
Or: 2.sin18° est irrationnel, alors que: (a - d) / (c - b) est rationnel
Donc on ne peut pas construire de pentagone équiangle avec des côtés entiers (sauf bien sûr si: a = b = c = d = e, ce qui donne le pentagone régulier).
#17 - 16-02-2015 22:04:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtzau 93
C'est ça Franky 
Vasimolo
#18 - 17-02-2015 18:24:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteauu 93
Il était amusant ce gâteau , non ?
Ma démonstration étant assez proche de celle de Franky , je vais vous épargner une deuxième lecture .
Un grand merci aux participants 
Gwen a levé un lièvre pour les polygones équiangles P à n côtés :
n premier <=> P nécessairement régulier
Une démonstration dans un sens ou dans l'autre ?
Vasimolo
#19 - 18-02-2015 15:40:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#20 - 18-02-2015 15:42:27
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Gteau 93
Je pense que: "n premier <=> P nécessairement régulier" n'est pas juste.
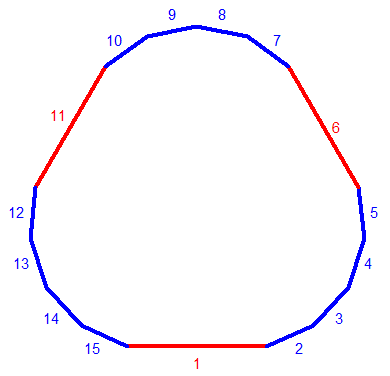
Je prends un octogone. Ses côtés entiers sont respectivement a, b, c, d, e, f, g et h
en tournant dans le sens des aiguilles d'une montre: ils sont parallèles deux à deux:
a//e, b//f, c//g et d//h. J'ai la relation: a.(V2/2)+b+c.(V2/2)=e.(V2/2)+f+g.(V2/2),
ce qui donne: (f-b)/(a+c-e-g)=V2/2, avec un membre rationnel et l'autre irrationnel.
Donc j'ai forcément: b=f, et je peux démontrer par rotation que: a=e, c=g et d=h.
Et l'octogone est forcément régulier, alors que 8 n'est pas premier.
Pour un décagone, il en va autrement et j'ai trouvé une petite astuce, mais cela fait l'objet d'une autre énigme.
Edit: Mon post contredit celui du pâtissier ci-dessus que je viens de lire. Mais le nombre 8 a la particularité de s'écrire 2³ et du coup, on n'aurait qu'un cercle sur le schéma.
#21 - 18-02-2015 15:49:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteu 93
Franky 
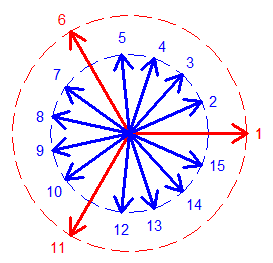
Tu reprends l'exemple précédent avec 4 flèches rouges et 4 flèches bleues et tu obtiendras un octogone equiangle non régulier .
Vasimolo
#22 - 18-02-2015 15:56:32
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gââteau 93
Côtés 1 2 1 2 1 2 1 2 par exemple.
Il est juste semi-régulier, si le terme existe...
#23 - 18-02-2015 16:11:42
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Gâteau 993
Au temps pour moi (ou autant pour moi, je n'ai jamais compris), avec a=e, b=f, c=g et d=h, j'ai simplement démontré que deux côtés parallèles sont égaux, mais pas du tout que l'octogone est régulier. Ma conclusion a été trop hâtive.
#24 - 18-02-2015 16:16:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea 93
Pas de problème Franky , seuls ceux qui osent proposer des solutions risquent de se tromper 
Vasimolo
#25 - 18-02-2015 16:19:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâreau 93
Oui, c'est pour ça que que c'est possible avec tout nombre de côtés non premier.
Multiple de 3 : on invente un truc avec n/3 côtés et on reporte sur un triangle équilatéral.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum