|
#1 - 25-02-2015 11:40:28
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Un décor qui mesuree
Bonjour à tous.
Une petite énigme pas bien méchante mais assez curieuse.
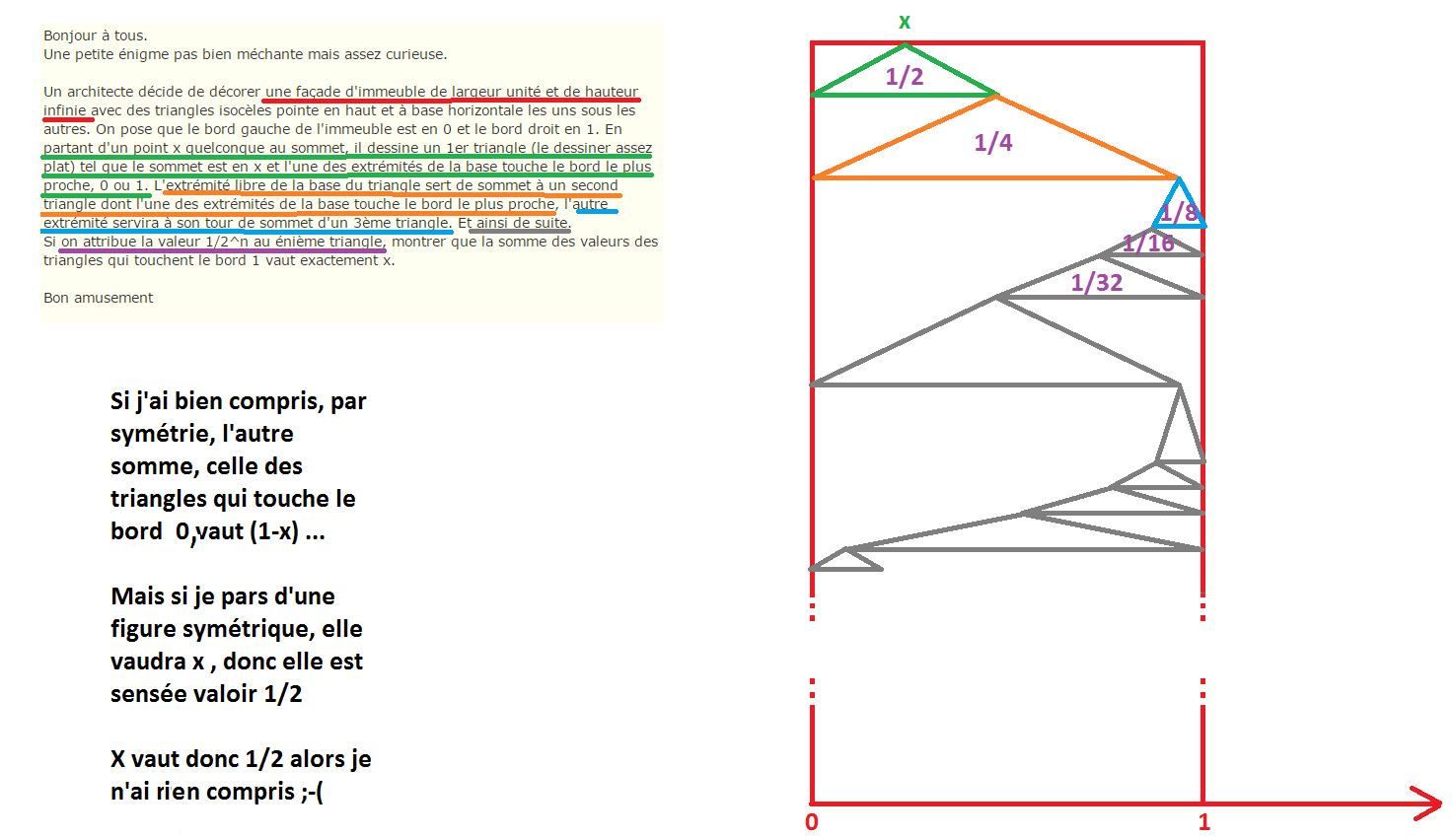
Un architecte décide de décorer une façade d'immeuble de largeur unité et de hauteur infinie avec des triangles isocèles pointe en haut et à base horizontale les uns sous les autres. On pose que le bord gauche de l'immeuble est en 0 et le bord droit en 1. En partant d'un point x quelconque au sommet, il dessine un 1er triangle (le dessiner assez plat) tel que le sommet est en x et l'une des extrémités de la base touche le bord le plus proche, 0 ou 1. L'extrémité libre de la base du triangle sert de sommet à un second triangle dont l'une des extrémités de la base touche le bord le plus proche, l'autre extrémité servira à son tour de sommet d'un 3ème triangle. Et ainsi de suite.
Si on attribue la valeur 1/2^n au énième triangle, montrer que la somme des valeurs des triangles qui touchent le bord 1 vaut exactement x.
Bon amusement
#2 - 25-02-2015 12:17:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
un décor qyi mesure
Rien compris non plus... Tu n'as pas un dessin ?
#3 - 25-02-2015 14:21:21
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
#4 - 25-02-2015 16:07:34
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Un décor qui mesre
Bravo Gwen pour le dessin, c'est exactement ça. De quelle manière puis je m'y prendre pour le copier et le mettre dans l'énoncé ?
#5 - 25-02-2015 16:09:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Un décor qqui mesure
Oui Gwen, si x est au milieu l'algorithme s'arrête immédiatement. Il y a d'autres cas particuliers, je ne veux pas en parler, je vous laisse les gérer. Mais l'idée est bien de chercher ce qu'il se passe pour un x quelconque.
PS: Gwen, ton dessin est peu encombrant en largeur, peux tu y faire quelque chose ?
#6 - 25-02-2015 17:07:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
un décor qui mesyre
Pas vraiment... C'était juste pour être sûr qu'on se comprenait bien. Et effectivement, la somme donne x. C'est d'ailleurs évident pour 1/2, 1/3 et 1/4
Je reviens plus tard...
#7 - 25-02-2015 17:45:49
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
nU décor qui mesure
Bonjour,
Je ne suis pas bien sûr d'avoir compris l'énoncé :
> les triangles isocèles successifs doivent-ils être semblables au premier ?
> que signifie la "valeur" d'un triangle ? est-ce l'abscisse de son sommet ?
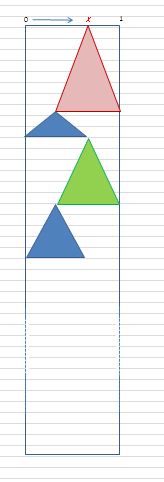
A suivre ! Merci !

Il aurait pu pleuvoir, con comme il est ! (Coluche)
#8 - 25-02-2015 18:05:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
yn décor qui mesure
Ca ressemble beaucoup à une écriture binaire du nombre x .
Un point x au sommet d'un immeuble infini : c'est le genre de phrase qui me décourage avant de commencer 
Vasimolo
#9 - 26-02-2015 09:37:01
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
un décor qui mequre
A NickoGecko: Ton dessin est correct. Les triangles isocèles peuvent prendre n'importe quelle forme pour la clarté de ton dessin. Ils pourraient être plats, mais ce serait vraiment illisible. Comme je l'ai dit dans l'énoncé, le 1er triangle en haut a pour valeur 1/2, celui en dessous 1/4, etc...Si le 1er triangle est collé contre le bord 1, alors 1/2 est à compter pour x.
A Vasimolo: ben oui, on calcule x en binaire. La hauteur est infinie pour beaucoup de valeurs de x. La hauteur est finie seulement pour les fractions dont le dénominateur est une puissance de 2 (vu qu'on additionne des puissances de 2).
A Titoufred: cette enigme est une partie de la réponse sur les mises à la banque.
C'est juste un petit problème d'arithmétique, cette énigme.
#10 - 28-02-2015 11:02:03
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Un décor qui mseure
Une autre présentation du problème:
Soit un segment [0;1], et un point x0 sur ce segment. On se propose d'ajouter les pts x1,x2,..xn de cette façon:
x(n+1) est le symétrique de 0 par rapport à xn si xn est plus proche de 0 que de 1.
x(n+1) est le symétrique de 1 par rapport à xn si xn est plus proche de 1 que de 0.
Si on attribue à xn la valeur 1/2^n, montrer que la somme des valeurs des xn symétriques de 1 est égale à x0.
#11 - 08-03-2015 16:16:27
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
#12 - 08-03-2015 19:04:56
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
un décor qui medure
Bonsoir Gwen,
J'ai proposé cette énigme sur un autre site, j'attends un peu pour donner une réponse ici. La démo est plutôt simple, ce n'est que de l'arithmétique de collège.
Indice: calculer et analyser les absisses des différents points successifs.
#13 - 10-03-2015 13:34:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Un déocr qui mesure
Dans le prolongement de la présentation du message 10:
Si x(n+1) est le symétrique de 0 par rapport à xn, alors x(n+1)=2xn
Si x(n+1) est le symétrique de 1 par rapport à xn, alors x(n+1)=xn-(1-xn)=2xn-1.
Remarquons que tous les x successifs sont dans l'ntervalle [0;1] c'est l'algorithme qui le veut comme ça.
Cela dit venons en tout de suite avec un exemple, où la suite des xn successifs est 0010.... (sous entendu symétrique de 0 ou 1).
x1=2x0
0<x1<1
0<2x0<1
0<x0<1/2.
x0<1/2, la valeur 1/2 est à compter dans 1-x0.
x2=2x1=4x0
0<4x0<1
0<x0<1/4=1-1/2-1/4 (borne inférieure inchangée).
la valeur 1/4 est à compter dans 1-x0
x3=2x2-1=8x0-1
0<8x0-1<1
1<8x0<2
1/8<x0<1/4 (borne supérieure inchangée)
la valeur 1/8 est à compter dans x0.
x4=2x3=16x0-2
0<16x0-2<1
2<16x0<3
1/8<x0<3/16=1/8+1/16 (borne inférieure inchangée)
la valeur 1/16 est à compter dans 1-x0.
etc...
On réduit l'intervalle de x0 à chaque itération:
Par un symétrique de 1,c'est la borne inférieure qui est modifiée.
Par un symétrique de 0, c'est la borne supérieure qui est modifiée.
Le cumul des valeurs des 1 successifs donne la valeur par défaut de x0.
Le cumul des valeurs des 0 successifs donne la valeur par défaut de 1-x0.
Dans notre exemple, le 1 au rang 3 dit que x0>1/8, et le zéro suivant que x0<1/8+1/16=3/16.
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum