Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 27-06-2015 22:12:26
Gâteau 010Bonjour à tous
#0 Pub#2 - 28-06-2015 02:28:16
Gâteau 1000J'espère que tu ne fais pas parti des correcteurs des oraux de mes concours "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #3 - 28-06-2015 12:33:41
fâteau 100Je n'ai pas le même résultat que toi , mais comme tu ne donnes pas ta stratégie je ne peux pas te dire s'il y a une erreur de méthode ou si le problème est mal compris . #4 - 28-06-2015 12:40:05#5 - 28-06-2015 13:03:12
Gâteu 100Excellente question Gwen #6 - 28-06-2015 16:13:54#7 - 29-06-2015 09:02:29#8 - 29-06-2015 17:44:20#9 - 30-06-2015 09:29:56
gâyeau 100Bonjour, Code:import sys
N=int(sys.argv[1])
ok={}; facto={}; tot=1
# ok[k] :
# Nb de cas où l'ensemble des lignes est connexe
# pour k couples de points.
# facto :
# Dictionnaire de factorielles, pour ne pas les
# recalculer.
# ko :
# Variable intermédiaire comptabilisant les cas
# à éliminer.
# Pour k couples de points, on élimine les
# permutations constituées d'un bloc
# connexe de moins de k lignes, suivi d'une
# permutation quelconque des autres points.
for k in range(1,N+1):
ko=0
tot*=k; facto[k]=tot
for k1 in range(1, k): ko+=ok[k1]*facto[k-k1]
ok[k]=tot-ko
print("N= %3d ok= %7d ko= %7d tot= %7d %7.3f %%"%(k,ok[k],ko,tot,(ok[k]/tot)*100))J'ai vérifié jusqu'à N=12 en simulant tous les cas possibles, mais le temps de calcul augmente très vite avec N (voir ci-dessous). Code:import sys
from itertools import permutations
N=int(sys.argv[1])
ko=tot=0
# permu :
# permu va parcourir toutes les permutations des
# nombres 0 à N-1.
# permu[i] est le n° du point de la ligne du bas
# relié au point n° i de la ligne du haut.
for permu in permutations(range(N),N):
tot+=1
jmax=-1
for i in range(N-1):
jmax=max(jmax,permu[i])
# jmax : n° du point le plus à droite de la ligne du bas
# parmi tous les points reliés aux points 0 à i
# de la ligne du haut (les numéros démarrent à 0).
# Si jmax=i, on a un bloc isolé de i+1 lignes.
if jmax==i: ko+=1; break
ok=tot-ko
print("N= %3d ok= %7d ko= %7d tot= %7d %7.3f %%"%(N,ok,ko,tot,(ok/tot*100)))Édité : Ajout de commentaires dans les scripts #10 - 30-06-2015 09:55:34#11 - 30-06-2015 18:04:22
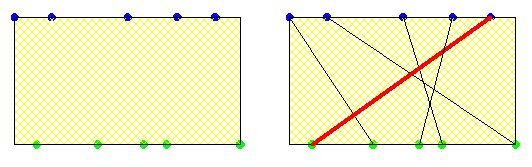
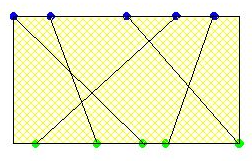
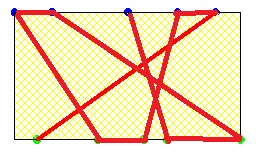
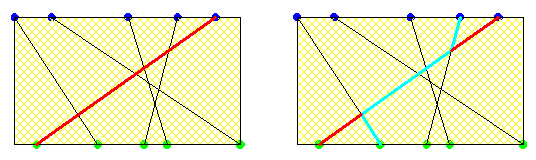
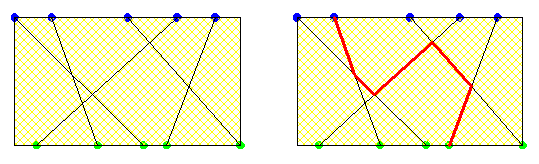
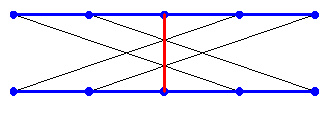
Gâteauu 100Si j'ai bien compris le problème la ligne rouge est la ligne qui se croise avec tous les autres lignes. #12 - 01-07-2015 20:23:55
gâteay 1001 chance sur 2500 : #13 - 01-07-2015 22:07:55#14 - 02-07-2015 00:30:29#15 - 02-07-2015 07:27:54
Gteau 100Dans mon message #9, j'ai supposé que l'on cherchait la probabilité que l'ensemble des lignes soit connexe. #16 - 03-07-2015 01:24:02
âteau 100Bonsoir à tous , j'ai été un peu en dessous de tout pour ce gâteau ( disons que j'ai eu des activités annexes #17 - 03-07-2015 06:46:14#18 - 03-07-2015 08:26:01
gâreau 100Voici un récapitulatif de ce que j'obtiens, pour N variant de 1 à 50 (voir mes messages #9 et #15) : Code:N= 1 proba_cas_1= 100.000 % proba_cas_2= 100.000 % N= 2 proba_cas_1= 50.000 % proba_cas_2= 50.000 % N= 3 proba_cas_1= 50.000 % proba_cas_2= 50.000 % N= 4 proba_cas_1= 41.667 % proba_cas_2= 54.167 % N= 5 proba_cas_1= 35.000 % proba_cas_2= 59.167 % N= 6 proba_cas_1= 30.000 % proba_cas_2= 64.028 % N= 7 proba_cas_1= 26.190 % proba_cas_2= 68.393 % N= 8 proba_cas_1= 23.214 % proba_cas_2= 72.155 % N= 9 proba_cas_1= 20.833 % proba_cas_2= 75.326 % N= 10 proba_cas_1= 18.889 % proba_cas_2= 77.969 % N= 11 proba_cas_1= 17.273 % proba_cas_2= 80.164 % N= 12 proba_cas_1= 15.909 % proba_cas_2= 81.992 % N= 13 proba_cas_1= 14.744 % proba_cas_2= 83.524 % N= 14 proba_cas_1= 13.736 % proba_cas_2= 84.819 % N= 15 proba_cas_1= 12.857 % proba_cas_2= 85.923 % N= 16 proba_cas_1= 12.083 % proba_cas_2= 86.875 % N= 17 proba_cas_1= 11.397 % proba_cas_2= 87.704 % N= 18 proba_cas_1= 10.784 % proba_cas_2= 88.431 % N= 19 proba_cas_1= 10.234 % proba_cas_2= 89.075 % N= 20 proba_cas_1= 9.737 % proba_cas_2= 89.650 % N= 21 proba_cas_1= 9.286 % proba_cas_2= 90.166 % N= 22 proba_cas_1= 8.874 % proba_cas_2= 90.632 % N= 23 proba_cas_1= 8.498 % proba_cas_2= 91.055 % N= 24 proba_cas_1= 8.152 % proba_cas_2= 91.441 % N= 25 proba_cas_1= 7.833 % proba_cas_2= 91.795 % N= 26 proba_cas_1= 7.538 % proba_cas_2= 92.121 % N= 27 proba_cas_1= 7.265 % proba_cas_2= 92.421 % N= 28 proba_cas_1= 7.011 % proba_cas_2= 92.699 % N= 29 proba_cas_1= 6.773 % proba_cas_2= 92.958 % N= 30 proba_cas_1= 6.552 % proba_cas_2= 93.198 % N= 31 proba_cas_1= 6.344 % proba_cas_2= 93.423 % N= 32 proba_cas_1= 6.149 % proba_cas_2= 93.633 % N= 33 proba_cas_1= 5.966 % proba_cas_2= 93.830 % N= 34 proba_cas_1= 5.793 % proba_cas_2= 94.015 % N= 35 proba_cas_1= 5.630 % proba_cas_2= 94.190 % N= 36 proba_cas_1= 5.476 % proba_cas_2= 94.354 % N= 37 proba_cas_1= 5.330 % proba_cas_2= 94.509 % N= 38 proba_cas_1= 5.192 % proba_cas_2= 94.657 % N= 39 proba_cas_1= 5.061 % proba_cas_2= 94.796 % N= 40 proba_cas_1= 4.936 % proba_cas_2= 94.928 % N= 41 proba_cas_1= 4.817 % proba_cas_2= 95.054 % N= 42 proba_cas_1= 4.704 % proba_cas_2= 95.173 % N= 43 proba_cas_1= 4.596 % proba_cas_2= 95.287 % N= 44 proba_cas_1= 4.493 % proba_cas_2= 95.396 % N= 45 proba_cas_1= 4.394 % proba_cas_2= 95.500 % N= 46 proba_cas_1= 4.300 % proba_cas_2= 95.599 % N= 47 proba_cas_1= 4.209 % proba_cas_2= 95.694 % N= 48 proba_cas_1= 4.122 % proba_cas_2= 95.785 % N= 49 proba_cas_1= 4.039 % proba_cas_2= 95.872 % N= 50 proba_cas_1= 3.959 % proba_cas_2= 95.955 % Pour le cas 1, j'ai le même résultat que scrablor en #17. Code:ok(1) = 1 ok(k) = k! - (Σ pour i=1→k-1)( ok(i) * (k-i)! ) #19 - 04-07-2015 20:40:59
Gâtea 100Enigmatus peut tu ajouter les commentaires sur tes programmes ? "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #20 - 04-07-2015 21:21:09
gâtrau 100Moi #21 - 05-07-2015 08:25:49#22 - 05-07-2015 09:06:19#23 - 05-07-2015 09:18:48#24 - 07-07-2015 23:20:21
Gâteua 100J'ai trouvé un peu de temps pour reprendre un peu de ce gâteau . #25 - 08-07-2015 06:41:53
gâreau 100@Vasimolo #24 : Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.