|
#1 - 17-09-2015 18:36:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 17-09-2015 19:10:34
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Gâtau 105
C'est impossible.
Si on donne une parité aux points, un trait de longueur impaire reliera un point pair à un point impair.
On a donc 5 points pairs et cinq points impairs qui restent.
Un trait de longueur paire reliera deux points de même parité.
On ne pourra donc jamais tracer le dernier trait.
#3 - 17-09-2015 21:01:33
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtea 105
Salut !
Je propose :
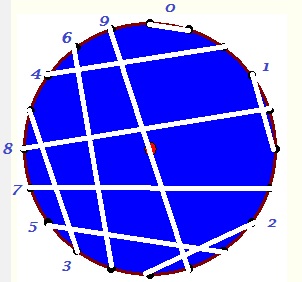
#4 - 17-09-2015 22:58:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 10
@Gwen : oui c'est l'idée 
@Golgot : il y a une petite erreur sur ton dessin .
Vasimolo
#5 - 17-09-2015 23:07:30
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 150
Ah oui, Zut ! 4 et 5 sont les mêmes... Mince, plus qu'à recommencer !
#6 - 18-09-2015 06:47:19
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtteau 105
Il n'y a pas de solution pour 20 parts.
Suite de Langford OEIS A014552
#7 - 18-09-2015 07:46:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtaeu 105
Tu peux préciser un peu Halloduda ? Je ne vois pas le rapport entre cette suite et notre problème .
Vasimolo
#8 - 18-09-2015 08:18:25
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteau 10
Il n'y a pas de solution pour 20 parts.
Si on numérote les positions successives sur le gâteau de 1 à 20,
les extrémités sont placées en x1, x1+1, x2, x2+2, ...x10, x10+10 toutes distinctes.
La somme des positions des 20 extrémités est égale à
2*somme des xi + 10*11/2, impair
Or elle est aussi égale à 20*21/2 = 210 pair
C'est impossible.
#9 - 18-09-2015 10:08:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 10
C'est ça Halloduda ( modulo 20 quand même  ) )
Vasimolo
#10 - 18-09-2015 11:25:11
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâtea u105
Salut !
Je ne comprends pas : ton gâteau pour 18 personnes compte 23 parts (en tout cas pas 18) !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#11 - 18-09-2015 13:00:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâeau 105
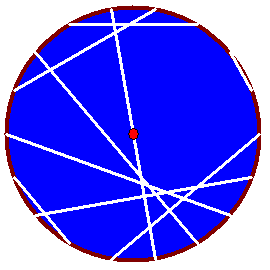
@Fix : les lignes blanches sont de simples décorations dont les extrémités indiquent les endroits où il faut couper .
Vasimolo
#12 - 19-09-2015 09:08:31
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
gâteai 105
Bonjour,
En numérotant les points sur la circonférence, on en a 10 de numéro impair, et 10 de numéro pair.
Les bâtons de sucre étant de tailles distinctes, leurs extrémités sont séparées respectivement par 1, 2, ... 10 intervalles (qu'on peut appeler la longueur du bâton).
Pour obtenir une longueur impaire (resp. paire), les numéros des extrémités doivent être de parité différente (resp. même parité).
Le dernier couple de points n'a pas la bonne parité, le gâteau pour 20 personnes n'est pas réalisable.
Un raisonnement analogue montre que :
- on ne peut pas réaliser des gâteaux pour 8k+4 ou 8k+6 personnes
- il est éventuellement possible (sans en être sûr) de réaliser des gâteaux pour 8k ou 8k+2 personnes
J'ai trouvé des solutions pour 2, 8, 10, 16 et 18 personnes.
#13 - 19-09-2015 11:57:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
hâteau 105
Bien vu Enigmatus 
Vasimolo
#14 - 19-09-2015 17:24:49
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
gâyeau 105
En numérotant les 20 points de 0 à 19 et en utilisant le même principe pour mesurer les angles orientés d'un cercle, mais on va remplacer modulo 2pi avec modulo 20
La plus grande distance entre deux points est 10 alors on a 10 distances différentes de 1 à 10
Une distance est la soustraction de deux nombres:
Si la distance est paire, ça implique que les deux nombres ont la même parité.
Si la distance est impaire, ça implique que les deux nombres ont une parité différente.
On a 20 nombres tel que 10 sont pairs et les 10 autres sont impairs.
On a 10 distances tel que 5 sont paires et les 5 autres sont impaires.
Une distance impaire va séparer un nombre pair et un nombre impair ce qui implique que 5 distances impaires vont séparer 5 couples (pair/impair)
Une distance paire va séparer 2 nombres pairs ou 2 nombres impairs.
Des 20 nombres du début il nous reste 10: 5 pairs et 5 impairs et il nous reste 5 distances paires, il n y a aucune répartitions des distances paires qui va lier les nombres restants car ces distances ne lient que couples du même parité donc le nombre des nombres pairs ou les nombres impairs doit être pair et puisque 5 est impair c'est impossible.
La réponse est impossible.
Bonne soirée.
#15 - 19-09-2015 19:26:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtteau 105
Oui Dbab 
Vasimolo
#16 - 20-09-2015 19:12:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtaeu 105
Je vous laisse lire les réponses , celle de Gwen résume bien le problème avec peu de moyen , mais les autres ne sont pas inintéressantes .
Merci aux participants .
Vasimolo
#17 - 21-09-2015 10:25:41
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#18 - 21-09-2015 16:26:04
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 1005
Lol, t'es pas tout seul, j'ai moi aussi chercher sans m'apercevoir que c'était impossible ! 
#19 - 21-09-2015 16:57:12
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gââteau 105
Perso, je ne comprends ni la question ni les réponses !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#20 - 21-09-2015 17:54:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 10
J'avais bien compris la question, mais je me suis vautré dans la recherche de la preuve de l'existence des solutions. J'aurais dû plus me méfier avec Vasimolo, car souvent ses énigmes trouvent une solution dans la parité...
Au fait, si ça ne marche pas avec des n différents de la forme 8n ou 8n+2, sait on prouver que ça marche tjs dans ces 2 cas là ?
#21 - 21-09-2015 18:21:54
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
Gâteau 015
Pour fix33:
En considérant que le cercle contient seulement 6 points, on numérote les points de 0 à 5 ,la distance entre les points est le bâton de sucre et c'est aussi la différence entre les valeurs des points en modulo 6, exemple pour une distance
5-0=5 c'est la distance entre 0 et 5 si on part de 0 vers 5 mais la vraie distance qu'on considère c'est 6-5=1 on change la valeur de 0 par 6 car on est dans un cercle et 0 vient juste après 5 dans ce cercle, on avait 1 et 5 comme distance mais on a choisi la plus petite.
En utilisant ce principe la plus grande distance est 3, alors les valeurs possibles pour une distance est 1 ou 2 ou 3
Une distance est la soustraction de deux nombres:
Si la distance est paire, ça implique que les deux nombres ont la même parité.
Exemple: 6-4=2 et 5-3=2
2 est une distance paire, on a 6 et 4 sont tous les deux pairs, 5 et 3 sont tous les 2 impairs
Si la distance est impaire, ça implique que les deux nombres ont une parité différente.
Exemple: 4-1=3 et 3-2=1
1 et 3 sont des distances impairs, on a 4 est pair et 1 est impair même chose pour 3 et 2
On a 0,2,4 sont des nombres pairs et 1,3,5 sont des nombres impairs
Donc on 3 nombre pairs et 3 nombres impairs
1,3 sont des distances impaires et 2 est une distance paire
Donc on a 2 distances impaires et une distance paire
Une distance impaire va lier un nombre pair avec un nombre impair
Alors 2 distances impaires vont lier 2 nombres pairs avec 2 nombres impairs
Après avoir utilisé les 2 distances impaires il va nous rester 2 nombres qui ne sont pas encore lié, ces deux nombres sont composé d'un nombre pair et un nombre impair. Il nous reste aussi une distance pair.
Le problème est qu'une distance paire ne peut pas lier un nombre pair et un nombre impair donc c'est impossible.
Vasimolo a précisé dans l'énoncé tous les bâtons de sucre étaient de tailles distinctes donc tous les distances doivent être différentes.
Le principe que j'ai utilisé pour le cercle de 6 points est le même qu'avec 20 points.
J'espère que j'étais assez clair.
Bonne soirée.
#22 - 21-09-2015 19:12:57
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
gâtzau 105
Merci dbab 
A vrai dire, je ne comprenais toujours pas le rôle des parts : c'est normal puisqu'elles n'en ont pas !
J'avais imaginé que les traits de sucre délimitaient les parts et je ne comprenaient pas que vous parliez de parité et de nombres entiers pour des longueurs de cordes...
Je vous rassure : la lumière s'est faite et j'ai compris ! 
Très astucieux de jouer sur la parité en effet !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#23 - 21-09-2015 19:15:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 1005
Et pourtant :
Vasimolo a écrit:@Fix : les lignes blanches sont de simples décorations dont les extrémités indiquent les endroits où il faut couper .
Vasimolo
#24 - 21-09-2015 19:31:53
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâtaeu 105
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#25 - 21-09-2015 20:45:12
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
gâteai 105
Sans vouloir t'offenser Vasimolo, c'est vrai que souvent tes explications nécessitent beaucoup de réflexions pour être comprises... Mais j'imagine que c'est volontaire et que c'est pour nous forcer à réfléchir encore un peu plus ! 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum