|
#1 - 12-10-2015 18:27:45
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
une énigme oour vous bluffer...
D'abord, désolé pour le titre racoleur, vous allez comprendre..
2 amis s'affrontent : Mr Rouge et Mr Bleu.
Chaque joueur met préalablement 10€ sur la table.
Puis, une boule (bleu ou rouge ) est retiré d'une urne contenant un grand nombre de boules . Si rouge est tiré, Mr Rouge gagne et inversement. En fonction de la répartition des boules dans l'urne, il y a une probabilité P connue de victoire pour Mr Rouge.
Avant que Mr Bleu prenne connaissance de la couleur de la boule, et pour compenser le fait que la probabilité de victoire P de Mr Rouge est inférieure à 50%, Mr Rouge est autorisé à prendre secrètement connaissance de la couleur de la boule. Il peut alors choisir d'ajouter une somme M préalablement définie sur la table pour "faire monter les enchères" ou pas.
S'il le fait, Mr Bleu a le droit d'abandonner la partie (Mr rouge emporte alors l'argent sur la table) ou bien "suivre la mise" en ajoutant cette même somme M sur la table. Dans ce cas, le "pot" constitué de l'ensemble des mises est attribué au vainqueur en fonction de la couleur de la boule.
Nos compères, qui sont des mathématiciens accomplis et savent jouer chacun de façon optimale constatent que pour M=6, le jeu est "équilibré", c'est à dire qu'aucun des joueurs n'est favorisé (leur espérance respective est nulle).
Quelle était donc la probabilité P de ce jeu ?
Réponse à exprimer en pourcentage ( cad. la probabilité multipliée par 100)
Question subsidiaire : Y a il des valeurs de P pour lesquelles aucune valeur de M ne permet d'équilibrer le jeu ?
#2 - 12-10-2015 23:09:37
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
une énigme pour vous bluffee...
Je ne comprends pas bien. Si Mr Rouge choisit d'ajouter la somme M préalablement définie sur la table, c'est parce qu'il sait que la couleur de la boule dont il a pris secrètement connaissance lui est favorable, sinon il ne le ferait pas. Dans ce cas, à chaque fois que Mr Rouge ajoute cette somme M, l'intérêt de Mr Bleu est d'abandonner et inversement.
#3 - 12-10-2015 23:16:59
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
une énigme pour vous blufder...
@Franky1103
Si l’intérêt de bleu est d'abandonner, pourquoi Rouge ne "miserait" pas quand il perd ? Ça lui ferait gagner plus, non ?
#4 - 12-10-2015 23:28:32
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
une énugme pour vous bluffer...
Ce n'est pas faux. Mr Rouge peut effectivement bluffer. Je réfléchis et je reviendrai.
#5 - 13-10-2015 12:03:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Une énigmee pour vous bluffer...
Pas compris l'énoncé. Rouge peut secrètement prendre connaissance de la couleur de la boule ?
#6 - 13-10-2015 12:18:10
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Une énimge pour vous bluffer...
Oui. Il peut alors :
- miser
* pour tenter d'augmenter son gain quand il a une boule gagnante (valorisation)
* tenter de faire abandonner son adversaire quand il est perdant : (mise en bluff)
- ne pas miser
Comme il a l'option de ne pas miser, on voit que cette option a une valeur positive au sens large. Mais a elle de la valeur ?
J'en ai profité pour essayer de clarifier l’énoncé : est ce mieux ?
#7 - 14-10-2015 09:59:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
une énigme pour vous bmuffer...
L'espérance de gain de B est donc égale à sa perte s'il passe son tour.
16x-16(1-x)=10
x=0,8125.
Ce n'est pas validé.
#8 - 14-10-2015 10:45:45
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Une énigme pour vous lbuffer...
@Nodgim
Au risque de dire moi même une bêtise, ce n'est pas validé car ce n'est pas juste...
Juste deux remarques :
-Le problème est plus complexe et nécessite en premier lieu la compréhension/résolution de la stratégie optimale des 2 joueurs.
Une petite piste : la stratégie des 2 joueurs est optimale si aucun des joueurs ne peut modifier sa stratégie de façon avantageuse par rapport à cette situation optimale d'équilibre.
- le gain / la perte et égale à ce que le joueur récupère moins ce qu'il a misé (ce qui ne semble pas correspondre à ta formule même si je ne comprends pas bien ce qu'elle signifie). C'est un jeu à somme nulle.
* Si il mise et est payé il gagne ou perds 16 suivant la boule tirée
* Si il mise mais n'est pas payé, il gagne 10 quelle que soit la boule tirée
* S'il ne mise pas, il gagne ou perd 10 suivant la boule tirée
#9 - 14-10-2015 22:36:20
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
une énigme pour vpus bluffer...
Comme Mr Rouge peut bluffer ou pas, il ajoutera la somme M une fois sur deux (et n’ajoutera donc rien une fois sur deux). De même, Mr Bleu suivra cette mise une fois sur deux (et abandonnera donc une fois sur deux).
Si une boule rouge est tirée, avec une probabilité P:
- Si Mr Rouge ajoute la somme M:
o Si Mr Bleu abandonne, alors Mr Rouge gagne 10, avec une probabilité P/4
o Si Mr Bleu suit la mise, alors Mr Rouge gagne 10+M, avec une probabilité P/4
- Si Mr Rouge n’ajoute rien, alors Mr Rouge gagne 10, avec une probabilité P/2
Si une boule bleue est tirée, avec une probabilité 1-P:
- Si Mr Rouge ajoute la somme M:
o Si Mr Bleu abandonne, alors Mr Rouge gagne 10, avec une probabilité (1-P)/4
o Si Mr Bleu suit la mise, alors Mr Bleu gagne 10+M, avec une probabilité (1-P)/4
- Si Mr Rouge n’ajoute rien, alors Mr Bleu gagne 10, avec une probabilité (1-P)/2
Le jeu est équilibré si l’espérance de gain est égale de part et d’autre:
P.(40+M)+(1-P).10 = (1-P).(30+M), soit P = (M+20)/(2.M+60)
Avec: M=6, on aura: P = 13/36, mais ma solution n’est pas validée.
J’ai dû me planter dans mes hypothèses de départ. Affaire à suivre …
#10 - 14-10-2015 23:37:29
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
unz énigme pour vous bluffer...
@Franky1103
plutôt bien raisonné...après la première hypothèse comme tu l'as deviné : pourquoi une fois sur 2 ?
En effet la probabilité optimale de bluff est variable. Par exemple : si la probabilité P=0, alors la fréquence de bluff optimale est trivialement 0. A l'inverse, si P=99% on voit bien qu'il peut bluffer 100% du temps sans qu'il ne puisse être rentable à son ami de suivre...La vérité est entre les 2...mais pas forcément au milieu, et a priori variable....
Si tu commences par déterminer les probabilités de bluff et de "suivi" en fonction de M et P tu pourras facilement conclure...
Si la méthode ne t’apparaît pas spontanément, je pense qu'une petite recherche sur les équilibres de Nash devrait aider...google est ton ami...
#11 - 15-10-2015 22:33:15
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
une énigme poyr vous bluffer...
Oh, j'avais pas vu, je m'y colle !
#12 - 16-10-2015 19:03:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
une énigle pour vous bluffer...
J'ai lu quelques articles intéressants sur l'équilibre de Nash, très utile en théorie des jeux. Mais je n'arrive même pas à construire la matrice du jeu entre Mr Rouge et Mr Bleu.
#13 - 16-10-2015 19:12:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
une énigme poue vous bluffer...
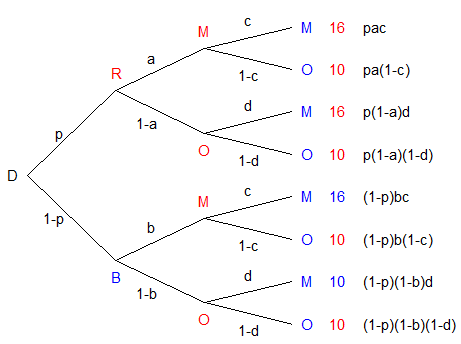
Je vais avoir un peu de temps pour chercher un peu , l'équilibre de Nash est souvent appliqué à l'économie et ça me gonfle un peu : heureusement il intervient aussi dans la théorie des jeux . Je ne sais pas si j'aurai le courage d'approfondir la chose mais j'ai fait un petit arbre de probabilité où l'on peut entrevoir certaines choses .
à suivre 
Vasimolo
#14 - 17-10-2015 19:01:54
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Une énigme pour vous bluffeer...
La methode est simple :
Il faut commencer par mettre en inconnues ( B et S par exemple) les probas respectives de bluffer et de suivre de nos amis pour construire le gain de Mr Rouge.(opposé à celui de Mr. Bleu )
A l'équilibre, aucun ne peut modifier sa proba de façon gagnante. Quelle implication en terme de dérivées partielles ?
Avec ca vous devriez pouvoir conclure facilement...
#15 - 18-10-2015 12:33:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Une éngme pour vous bluffer...
J'ai attaqué les calculs et j'arrive à une probabilité P=5/13 ( environ 38% ) qui n'est pas validée par la case réponse 
Vasimolo
#16 - 18-10-2015 19:26:41
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Une énigme pour vous buffer...
On appelle S la probabilité de suivre pour M. Bleu lorsque M. Rouge mise.
M. Bleu a intérêt à suivre suffisamment souvent pour qu'un bluff de M. Rouge devienne inefficace, mais pas trop car sinon il va perdre de l'argent lorsque M. Rouge mise pour valeur. A l'équilibre stratégique, rien ne doit changer quant à l'espérance de gain, que M. Rouge bluffe ou pas (sinon M. Rouge aurait intérêt a changer sa part de bluff).
Lorsqu'une boule bleue est tirée :
Si M. Rouge bluffe, son espérance de gain est égale à (1-S)10-S(10+M)
S'il ne bluffe pas, son espérance de gain est égale à -10
La résolution de l'équation (1-S)10-S(10+M)=-10 donne S=20/(20+M)
Dès lors, l'espérance de gain de M. Rouge sur une partie est égale à PS(10+M)+P(1-S)10-(1-P)10, ce qui donne après simplification P(MS+20)-10.
Si le jeu est équitable , on en déduit que P=10/(MS+20) et puisque S=20/(20+M), alors P=(20+M)/(40+4M)
Pour M=6, on trouve P=13/32=40,625%.
#17 - 18-10-2015 20:05:29
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Une énigmme pour vous bluffer...
J'ai un peu de mal à suivre le raisonnement, mais cette valeur est validée.
P = (20+M) / (40+4M) donne: M = (20-40P) / (4P-1)
Donc, pour P = 25%, aucune valeur de M ne permet d'équilibrer le jeu.
#18 - 18-10-2015 21:44:57
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Une éénigme pour vous bluffer...
Oui Franky, on peut ajouter que pour P>1/2 et P<1/4, la solution trouvée pour M est négative, ce qui ne fournit pas une solution acceptable dans le contexte du problème.
Remarque : Quoique, pour P<=1/4, le jeu pourrait être rendu équitable si l'on autorisait une mise négative à M. Rouge, la mise devant alors être égale à (20P-10)/(1-P). Cette mise négative étant alors interprétée comme la possibilité de reprendre de l'argent mis au milieu.
#19 - 19-10-2015 11:38:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Une énigme pour ous bluffer...
#20 - 19-10-2015 15:15:40
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Une énigme pour vous blufer...
J'ai un peu modifié mes explications, je ne sais pas si c'est plus clair. Sur quelle partie y a-t-il besoin d'eclaircissements ?
@Vasimolo : c'est ça mais tu peux simplifier ton arbre. Si la boule tirée est rouge, M. Rouge ne peut que miser, ne pas miser serait stupide. Et si la boule est bleue et que M. Rouge ne bluffe pas alors, M. Bleu gagne automatiquement.
#21 - 19-10-2015 18:00:37
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Une énigme pour vous bluffer....
Bravo @titoufred !!
Ta méthode de résolution est très synthétique et rapide. Ta remarque à @vasimolo est tout à fait juste.
Effectivement, les valeurs P=25% et P=50% ont une explication qualitative amusante :
Pour P<=25%, la « bluff equity » ne peut pas compenser le désavantage initial : on est trop loin de l’équilibre. Dans ce cas, il faut changer l’arbre et mettre une mise négative qui est toujours retenue dans le cas perdant, parfois dans le cas gagnant. Un concept pas si absurde, un peu à la manière d’une souscription d’assurance.
L’arbre général de @vasimolo est peut-être en fait très utile pour appréhender les cas frontières car on car on a, ou non, des solutions à M positif et négatif pour équilibrer le jeu en fonction de P, un M positif pour « bluffer » et un M négatif pour « assurer ». Je vais essayer de me plonger à ce cas général.
En avant-première, on voit trivialement que dans le cas M=-10, on arrive à surmonter le cas P=0…Cette solution est donc plus puissante que le mise en bluff pour des valeurs faibles de P…
Pour P>=50%, il est toujours mieux de rester avec P que de revenir à 50% donc ce cas n’est donc pas intéressant à étudier.
Perso, j’ai résolu le problème de manière plus générale et moins élégante dans ce cas particulier. La méthode est toutefois intéressante je donne l’idée :
- expliciter l’arbre de décision pour écrire l’équation paramétrée du Gain de A (= -Gain de B).
- L’équilibre implique que les dérivées partielle en %Bluff et %suivi soit nulles (et les dérivées secondes négatives mais il s’agit plus d’une vérification que d’une contrainte)
- Réinjecter ces valeurs dans l’équation initiale quand Gain=0 et conclure.
#22 - 19-10-2015 18:20:07
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
une énigme pour vous bliffer...
Un autre problème dans ton arbre, @vasimolo : dans le cas ou il n'y a pas de mise, il ne s'agit pas pour le deuxième joueur de suivre ou pas... On donne juste le pot au gagnant.
#23 - 19-10-2015 18:28:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Une énigme opur vous bluffer...
titoufred a écrit:@Vasimolo : c'est ça mais tu peux simplifier ton arbre. Si la boule tirée est rouge, M. Rouge ne peut que miser, ne pas miser serait stupide. Et si la boule est bleue et que M. Rouge ne bluffe pas alors, M. Bleu gagne automatiquement.
Non en fait les règles n'était pas claires et ne le sont toujours pas pour moi . Faut-il comprendre que si Rouge ne mise pas le jeu s'arrête avec gain pour Bleu ?
Vasimolo
#24 - 19-10-2015 18:32:29
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
unz énigme pour vous bluffer...
Quand pas de mise, le jeu s’arrête avec gain pour le Mr Bleu si boule bleue,gain pour Mr Rouge si boule rouge : pas de bluff, juste le meilleur gagne...
En pratique ,comme il mise toujours quand il a la bonne boule, ce cas ne s'applique effectivement que quand il perd
#25 - 19-10-2015 18:37:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Une énigme pour vous bluuffer...
@Portugal : nos messages se sont croisés 
Le jeu que je propose n'est pas complètement ridicule même s'il est loin du Poker .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum