 |
#1 - 17-09-2016 16:47:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facterus pour un milliard
Bonjour à tous,
Combien y a t'il de triplets distincts d'entiers naturels (a,b,c) a <= b <= c dont le produit vaut 1 milliard ?
Enigme inspirée par un problème scolaire légèrement modifié.
Comptez bien !
#2 - 17-09-2016 19:40:08
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
3 facteurs poir un milliard
10^9=2^9*5^9
Avec deux nombres formés à partir des puissances de deux on a :
(2, 2^8, 5^9) ; (2^2, 2^7, 5^9) ; (2^3, 2^6, 5^9) et (2^4, 2^5, 5^9)
Avec deux nombres formés à partir des puissances de cinq on a :
(2^9, 5, 5^8) ; (2^9, 5^2, 5^7) ; (2^9, 5^3, 5^6) et (2^9, 5^4, 5^5)
Et la tâche la plus délicate trouver les nombres en communs avec une puissance de 2 et une puissance de 5 :
(2, 2^8*5, 5^8) ; (2, 2^8*5^2, 5^7) ; (2, 2^8*5^3, 5^6) ; (2, 2^8*5^4, 5^5)
Ensuite on réitère l'opération jusqu'à 2^9 en premier ce qui donne au total 4*9 triplets et il faut faire fois deux avec les puissances de 5 pouvant varier comme celles de deux, entre 1 et 9.
Donc si j'ai bien compté ça nous fait 4*9*2 + 2*4 = 80 triplets distincts de nombres distincts. A mon avis il m'en manque encore quelques uns.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#3 - 17-09-2016 21:14:25
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
3 facteurs pouur un milliard
Bonjour,
[TeX]1 000 000 000 = 10^9 = 2^95^9[/TeX]
Pour répartir les 2 de manière ordonnée, on a:
1 manière avec un 9 pour plus grand nombre
1 manière avec un 8 pour plus grand nombre
2 avec un 7
2 avec 6
3 avec 5
2 avec 4
1 avec 3
Soit 12 manières en tout.
Parmi ces manières, il y en a une ou les trois facteurs possèdent autant de 2, 5 avec une paire (de 0 à 4, 5x2 dépassant 9)
Donc 0 tout pareil, 5 avec paire, 7 tout différent.
Si les 2 sont équirépartis, les 5 doivent être tous distincts, soient 7x1 possibilités
Si les 2 sont tous différents, les 5 peuvent être sous n'importe quelle configuration, soit 55x7 possibilités (1+2+...+10)
Si il y a une paire au niveau des deux, il ne doit pas y avoir de paire qui coïncide au niveau des 5, soit exactement 7 répartitions qui ne vont pas pour chaque. On a alors (55-7)*5 = 48*5
On trouve au final 7 + 55x7 + 48x5 = 632 sauf erreur de ma part.
Ca pourrait être utile de mettre une case réponse...
Edit:
J'ai trouvé mon erreur, j'ai compté le triplet (3,3,3) dans les paires, on a donc 7 + 55x7 + 48x4 = 584 en espérant qu'il n'y ait plus d'erreurs...
#4 - 17-09-2016 21:47:22
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
3 fcteurs pour un milliard
Bonsoir,
Sauf erreur, j'en trouve 517.
#5 - 18-09-2016 08:11:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs pour un miliard
@ Shadock: il t'en manque (beaucoup)
@ Caduk : tu dois avoir des redondances, c'est trop fort.
@ Enigmatus : C'est le bon nombre, et la 1ère bonne réponse, bravo !
#6 - 18-09-2016 09:15:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,033E+3
3 facteurs pour un imlliard
Il semble y en avoir (édit) 517.
#7 - 18-09-2016 11:44:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs pour un millaird
C'est une bonne réponse Gwen, bravo !
#8 - 18-09-2016 12:13:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,033E+3
3 facteurs puor un milliard
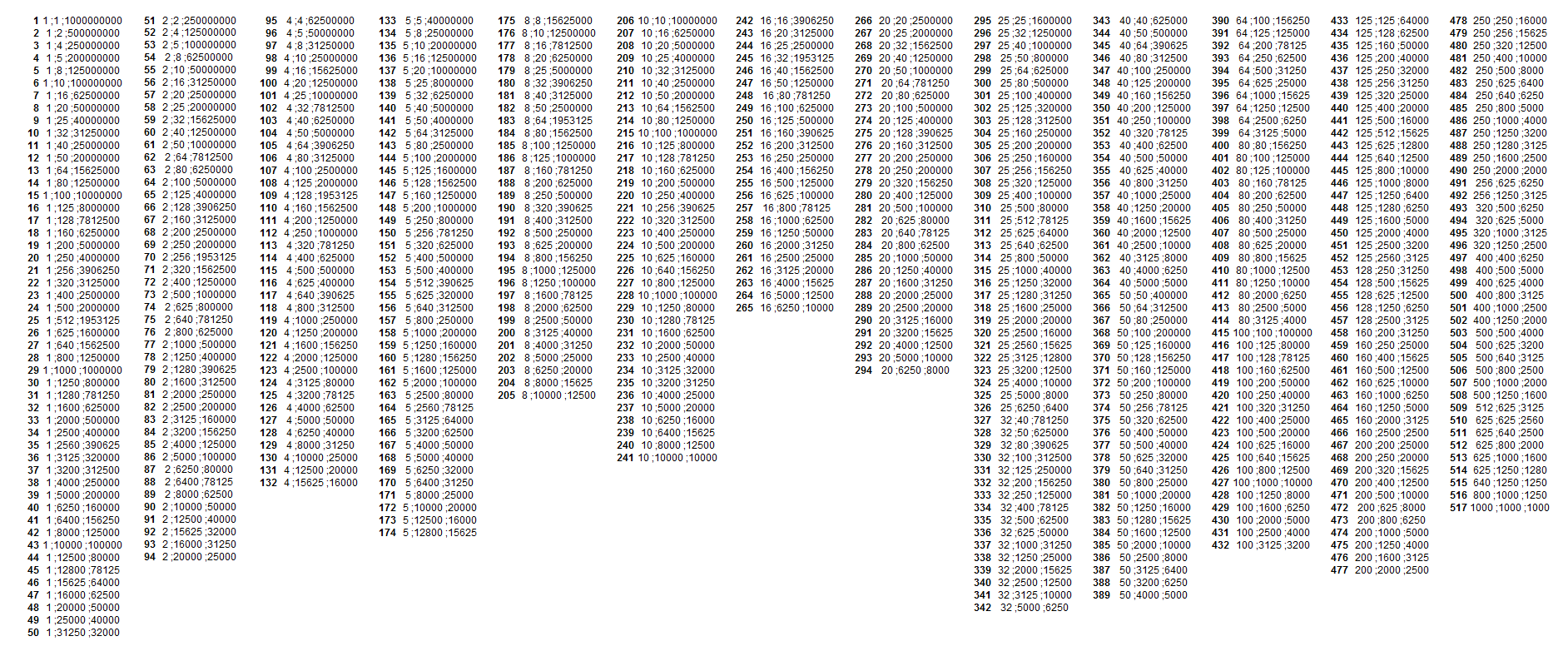
Le premier terme est un diviseur de 1 000 000 000 inférieur ou égal à 1000 , ce qui en laisse 29.
Le second est inférieur ou égal à la racine de ce qui reste et supérieur ou égal au premier, mais le plus simple est de lister les diviseurs du reste.
Par exemple : pour un premier terme égal à 20 , il reste 50 000 000 qui a 72 diviseurs allant par paire. Cela en laisse 36 potentiels auxquels il faut retirer ceux qui sont inférieurs à 20 : 1 2 4 5 8 10 16.
20 amène donc 29 triplets.
C'est assez rapide à faire. (j'avais juste négligé les carrés au début)
Pour les lister, excell est quand même bien pratique.
#9 - 18-09-2016 13:02:25
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs pour nu milliard
D'accord Gwen.
On peut envisager une généralité pour toutes les puissances d'un nombre ayant 2 facteurs premiers dans sa décomposition.....
#10 - 18-09-2016 16:53:03
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
3 facteurss pour un milliard
Bonjour nodgim,
J'en trouve 517.
#11 - 18-09-2016 18:54:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs pour un miliard
Francky, c'est bien ça bravo !
#12 - 18-09-2016 19:25:35
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
3 facteurs pour un illiard
Je trouve 517, par deux moyens différents mais fort peu élégants (programme, énumération manuelle).
Je suis curieux de voir une solution moins bourrin.
#13 - 19-09-2016 08:28:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs pour un millirad
Ebichu, c'est le bon nombre également, bravo !
@ tous :
Si je demande la même question avec 10^50, sauriez vous trouver la réponse dans un temps raisonnable (disons 1/4 heure) sans informatique ?
#14 - 19-09-2016 18:54:06
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,033E+3
3 facteurs pour un milliardd
Avec la formule, oui: 293 384 
#15 - 19-09-2016 19:36:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
3 facteurs oour un milliard
J'ai compris le truc.
Un diviseur de 10^n est de la forme 2^a.5^b. On recherche donc tous les triplets de couples (a1;b1) (a2;b2) (a3;b3) tels que a1+a2+a3=n et b1+b2+b3=n.
Reprenons l'exemple du milliard, pour lequel n=9. On peut partitionner 9 en 12 sommes différentes. Parmi ces 12 partitions, une est du type XXX (c'est 3+3+3), 4 sont du type XXY (0+0+9 ; 1+1+7 ; 2+2+5 et 4+4+1) et les 7 autres du type XYZ (0+1+8 ; etc).
Ensuite, il faut choisir une partition pour a1+a2+a3, et une partition pour b1+b2+b3, par exemple, 0+3+6 et 1+1+7 ; puis on se demande combien il y a de triplets correspondants qui donnent 1 milliard. Il y a 2^0.5^1 ; 2^3.5^1 ; 2^6.5^7, mais aussi 2^0.5^1 ; 2^3.5^7 ; 2^6.5^1, et enfin 2^0.5^7 ; 2^3.5^1 ; 2^6.5^1.
D'une manière générale, pour une partition du type XYZ et une partition du type XXY, il y a 3 triplets. Plus généralement, on peut établir une table :
XXX et XXX => 1 triplet
XXX et XXY => 1 triplet
XXX et XYZ => 1 triplet
XXY et XXY => 2 triplets
XXY et XYZ => 3 triplets
XYZ et XYZ => 6 triplets
Si maintenant on appelle x le nombre de partitions du type XXX, y le nombre de partitions du type XXY, et z le nombre de partitions du type XYZ (on a donc x=1, y=4 et z=7 pour le cas n=9), on va avoir en tout x(x+y+z)+y(x+2y+3z)+z(x+3y+6z) triplets. Par exemple, le terme z(x+3y+6z) provient de ce que chacune des z partitions possibles de type XYZ pour a1+a2+a3 peut rencontrer x partitions de type XXX pour b1+b2+b3, chacune donnant 1 triplet, y partitions de type XXY pour b1+b2+b3, chacune donnant 3 triplets, et z partitions de type XYZ pour b1+b2+b3, chacune donnant 6 triplets.
Ce qui donne après développement x²+2y²+6z²+2xy+2xz+6yz triplets, et on retrouve bien 517 en remplaçant x, y et z par 1, 4 et 7.
En général (pour n valant autre chose que 9), en notant E la fonction partie entière par défaut,
x vaut 1 si n est multiple de 3 et 0 sinon,
y vaut E(n/2)+1-x,
et z vaut E((n²+3)/12) (merci https://oeis.org/A001399 ).
Pour n=50, on a x=0, y=26, et z=208, et la réponse est 293384.
#16 - 20-09-2016 08:26:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs opur un milliard
Ebichu, c'est bien aussi comme ça que j'ai compté, bravo !
Pour le cas 10^50, je me demande si tu n'as pas donné par erreur pour z la valeur y + z ?
#17 - 20-09-2016 09:55:18
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
3 factrurs pour un milliard
Je ne pense pas qu'il y ait d'erreur, j'aurais dû plus détailler la fin.
https://oeis.org/A001399 donne que x+y+z = 1+E((n^2+6*n)/12), d'où z = 1+E((n^2+6*n)/12)-(x+y) = 1+E((n^2+6*n)/12)-(E(n/2)+1) = E((n²+3)/12).
Pour n=50, cela donne x+y+z=234, ce qui correspond bien au nombre de partitions donné par OEIS.
Et pour finir, en programmant ma formule sur le tableur, j'ai obtenu la suite des réponses pour toutes les valeurs de n, suite qui coïcide avec... https://oeis.org/A101427 ! On trouve tout sur OEIS, ça fait peur...
#18 - 20-09-2016 10:52:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facteurs pour un mliliard
C'est OK, Ebichu. Curieusement j'avais fait une erreur simple dans une somme qui donnait étrangement 208 au lieu de 234 (on peut facilement trouver z sans OEIS, à condition de ne pas se planter dans les opérations..)
#19 - 20-09-2016 15:00:33
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
3 facteurs pour yn milliard
Voici mes résultats:
1 : 1
10 : 2
100 : 8
1000 : 19
10000 : 42
100000 : 78
1000000 : 139
10000000 : 224
100000000 : 350
1000000000 : 517
10000000000 : 744
100000000000 : 1032
1000000000000 : 1405
10000000000000 : 1862
100000000000000 : 2432
1000000000000000 : 3115
10000000000000000 : 3942
100000000000000000 : 4914
1000000000000000000 : 6067
et puis en cherchant OEIS, on trouve: A101427
Donc la solution est 517.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#20 - 20-09-2016 15:38:47
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
3 faxteurs pour un milliard
Si on poursuit un peu plus loin pour 10^n:
0: 1
1: 2
2: 8
3: 19
4: 42
5: 78
6: 139
7: 224
8: 350
9: 517
10: 744
11: 1032
12: 1405
13: 1862
14: 2432
15: 3115
16: 3942
17: 4914
18: 6067
19: 7400
20: 8954
21: 10729
22: 12768
23: 15072
24: 17689
25: 20618
26: 23912
27: 27571
28: 31650
29: 36150
30: 41131
31: 46592
32: 52598
33: 59149
34: 66312
35: 74088
36: 82549
37: 91694
38: 101600
39: 112267
40: 123774
41: 136122
42: 149395
43: 163592
44: 178802
45: 195025
46: 212352
47: 230784
48: 250417
49: 271250
50: 293384
51: 316819
52: 341658
53: 367902
54: 395659
55: 424928
56: 455822
57: 488341
58: 522600
59: 558600
60: 596461
61: 636182
62: 677888
63: 721579
64: 767382
65: 815298
66: 865459
67: 917864
68: 972650
69: 1029817
70: 1089504
71: 1151712
72: 1216585
73: 1284122
74: 1354472
75: 1427635
76: 1503762
77: 1582854
78: 1665067
79: 1750400
80: 1839014
81: 1930909
82: 2026248
83: 2125032
84: 2227429
85: 2333438
86: 2443232
87: 2556811
88: 2674350
89: 2795850
90: 2921491
91: 3051272
92: 3185378
93: 3323809
94: 3466752
95: 3614208
96: 3766369
97: 3923234
98: 4085000
99: 4251667
100: 4423434
101: 4600302
102: 4782475
103: 4969952
104: 5162942
105: 5361445
106: 5565672
107: 5775624
108: 5991517
109: 6213350
110: 6441344
111: 6675499
112: 6916038
113: 7162962
114: 7416499
115: 7676648
116: 7943642
117: 8217481
118: 8498400
119: 8786400
120: 9081721
121: 9384362
122: 9694568
123: 10012339
124: 10337922
125: 10671318
126: 11012779
127: 11362304
128: 11720150
129: 12086317
130: 12461064
131: 12844392
132: 13236565
133: 13637582
134: 14047712
135: 14466955
136: 14895582
137: 15333594
138: 15781267
139: 16238600
140: 16705874
141: 17183089
142: 17670528
143: 18168192
144: 18676369
145: 19195058
146: 19724552
147: 20264851
148: 20816250
149: 21378750
150: 21952651
151: 22537952
152: 23134958
153: 23743669
154: 24364392
155: 24997128
156: 25642189
157: 26299574
158: 26969600
159: 27652267
160: 28347894
161: 29056482
162: 29778355
163: 30513512
164: 31262282
165: 32024665
166: 32800992
167: 33591264
168: 34395817
169: 35214650
170: 36048104
171: 36896179
172: 37759218
173: 38637222
174: 39530539
175: 40439168
176: 41363462
177: 42303421
178: 43259400
179: 44231400
180: 45219781
181: 46224542
182: 47246048
183: 48284299
184: 49339662
185: 50412138
186: 51502099
187: 52609544
188: 53734850
189: 54878017
190: 56039424
191: 57219072
192: 58417345
193: 59634242
194: 60870152
195: 62125075
196: 63399402
197: 64693134
198: 66006667
199: 67340000
200: 68693534
201: 70067269
202: 71461608
203: 72876552
204: 74312509
205: 75769478
206: 77247872
207: 78747691
208: 80269350
209: 81812850
210: 83378611
211: 84966632
212: 86577338
213: 88210729
214: 89867232
215: 91546848
216: 93250009
217: 94976714
218: 96727400
219: 98502067
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#21 - 20-09-2016 16:12:22
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facturs pour un milliard
Merci pour cette liste, Dhrm77.
Dans ma réponse, je te montrerai que le nombre de triplets se déduit du nombre de zéros par un polynome de degré 4.
#22 - 20-09-2016 18:49:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3812
3 facreurs pour un milliard
Le temps imparti est maintenant écoulé, vous pouvez tous regarder la méthode d' Ebichu, qui permet d'arriver rapidement au résultat sans gros calcul ni informatique. On peut facilement retrouver le calcul de x + y + z sans même se servir de la formule donnée par OEIS.
Sinon, le résultat demandé était bien 517, ce que vous avez tous trouvé.
Pour le fun, je m'étais amusé à calculer le nombre de triplets quand la puissance vaut 6 k : 54 k ^ 4 + 54 k ^ 3 + 24 k ² + 6 k + 1.
On peut le faire pour les 5 autres valeurs, de 6k+1 à 6k+5, mais ce n'est pas très intéressant.
Merci de votre participation, et à la prochaine énigme.
#23 - 20-09-2016 19:05:10
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
3 facteurs pour un mikliard
Pour ma part, j'utilise la formule suivante:
Etant donné les 8 premiers nombres de la serie (A(0)=1.... A(7)=224),
on a A(8) = A(7) + 2A(6) - A(5) - 2A(4) - A(3) + 2A(2) + A(1) - A(0) + 12
ou pour un element quelconque:
A(n) = A(n-1) + 2A(n-2) - A(n-3) - 2A(n-4) - A(n-5) + 2A(n-6) + A(n-7) - A(n-8) + 12
on peut egalement etendre la serie a l'envers....
A(0) = A(7) + 2A(6) - A(5) - 2A(4) - A(3) + 2A(2) + A(1) - A(8) + 12
et on voit que la serie est reflétée:
8 = a(-5)
2 = a(-4)
1 = a(-3)
0 = a(-2)
0 = a(-1)
1 = a(0)
2 = a(1)
8 = a(2)
ce qui n'a pas forcement un sens logique...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
|
 |

 Accueil
Accueil
 Forum
Forum







