Enigme 100 coffres (logique et probas) @ Prise2Tete

scarta · #1

Dans une salle se trouvent 100 coffres numérotés (de 1 à 100).
A l'intérieur de chacun se trouve une certaine somme, entre 1 et 100€.
Toutes les sommes sont différentes et le coffre N ne contient pas nécessairement N €.

Une première personne entre dans la salle. Elle peut ouvrir tous les coffres. Elle peut aussi choisir 2 coffres et échanger leur contenus. Deux coffres, pas plus.
Ensuite elle ressort.

Une deuxième personne entre derrière. On lui demande d'ouvrir le coffre qui contient X euros. Elle a bien sûr défini une stratégie avec la première personne pour trouver ce coffre le plus vite possible.

Partie logique :
- quelle est cette stratégie ?
- combien de coffres à ouvrir cela fait il, au pire des cas ?

Partie probabilités :
- quelle est l'espérance de la variable aléatoire "nombre de coffres à ouvrir"?
(Plus simplement, combien de coffres faudra t'il ouvrir en moyenne)
- quelle est l'espérance de la variable aléatoire "nombre maximal de coffres à ouvrir"?
(Autrement dit, la moyenne de tous les pire cas)

Édit: je pensais avoir la réponse mais en fait non ... je cherche encore.
Edit2: j'ai la réponse
Maintenant, si quelqu'un aune formule qui évite 40 minutes de calculs informatisés je prends !
La case réponse valide ab,cd-ef,gh avec ab,cd le nombre de coffres moyen à ouvrir; et ef,gh la moyenne des pires cas; à chaque fois arrondi au centième.

gwen27 · #2

Pour la partie "logique" , je dirais pas plus de 50 coffres à ouvrir, vu qu'en échangeant deux contenus judicieusement choisis, on peut diviser une "boucle" par 2, avec l'assurance que chaque coffre soit dans sa propre boucle.

Au pire, donc 100/2 = 50 s'il n'a vraiment pas de bol ! (il commence bien sûr par ouvrir le coffre dont le numéro est la somme qu'il cherche, pour s'assurer d'être dans la bonne boucle, puis se laisse guider par les sommes trouvées.)

Pour la partie proba, je laisse ça à d'autres mais on doit être autour d'une trentaine de coffres en moyenne.

Un exemple pour 13 coffres :

Code:

1  2  3  4  5  6  7   8  9  10  11  12 13
5  7  6 10  1  8  4  13  2  12  11   9  3

Donne les boucles :

Code:

(1 5)  (2 7  4 10 12 9)  (3 6  8 13)  (11)
(5 1)  (7 4 10 12  9 2)  (6 8 13  3)  (11)

ce qui en suivant la stratégie « j'ouvre le coffre portant le numéro de ma somme, puis celui de la somme trouvée dedans ….etc » oblige à ouvrir jusqu'à 6 coffres presque une fois sur 2, soit une moyenne de 4,75 coffres ouverts.

On voit que chaque numéro de coffre est obligatoirement dans la boucle du coffre qui contient cette somme.
Il suffit de couper en 2 la plus grande boucle.

(2 7 4 10 12 9)
(7 4 10 12 9 2)

Et on la réduit de moitié :

Code:

(1 5)  (2 7 4) (10 12  9)  (3 6  8 13)  (11)
(5 1)  (7 4 2) (12  9 10)  (6 8 13  3)  (11)

Le maximum de coffres ouverts passe à 4 , à peine une fois sur 3, pour une moyenne qui passe à 3,25 coffres ouverts.

scarta · #3

Bravo pour la partie logique c'est bien ça.
Edit: bon c'est pas gagné pour les probas, je viens de me rendre compte qu'il y a possibilité d'incompréhension... j'ai corrigé ça. Du coup, si tu as quasi bon pour la moyenne des pires cas, ce n'est pas ça du tout pour la moyenne globale

caduk · #4

Bonjour,
Je pense que la meilleure stratégie est de suivre le cycle formé en ouvrant le coffre dont le numéro est la valeur du dernier coffre ouvert.
Le pire des cas est celui ou le cycle ne se referme que après avoir visité tout les coffres. Une transposition permet de se ramener à deux cycles de 50, ce qui ramène le pire des cas à 50 coffres ouverts. De même, si le plus grand cycle dans la décomposition en cycles est supérieur à 50, on pourra le diviser en deux cycles plus petit.
Même si j'ai la forte intuition que c'est la meilleure stratégie, je n'en suis pas totalement convaincu, mais j'ai des pistes pour le démontrer.

Dr.Robotnik · #5

Partie logique :
Une stratégie qu'ils pourraient utilisé serais de
déplacer un billet de valeur V prévu à l'avance
dans un coffres C prévu à l'avance , ainsi
si on lui demandais V euros cette personne trouverais imédiatement
le billet dans le coffre C , et pour toutes les autres valeurs
cette personne au pire ouvrira 99 coffres .

Partie probabilité :
- quelle est l'espérance de la variable aléatoire "nombre de coffres à ouvrir"?
E(X)=((99*100)/2)*(99/100^2)+(1/100)=49.015
la seconde question n'est pas très clair , les pires cas
sont considérés comme 99 coffres à ouvrir avec cette stratégie
ou comme la somme de tout les cas où le nombre de coffres
à ouvrir est supérieur à 1 ?

scarta · #6

@caduk, la stratégie est la bonne. Aux probabilités maintenant
@Dr.R, il y a plus efficace

Dr.Robotnik · #7

40 minutes de calcul ?

scarta · #8

Avec une bonne couche d'optimisation, oui c'est le temps qu'il a fallu pour calculer le nombre d'essais moyen

Dr.Robotnik · #9

Personne n'as trouvé la réponse ?

scarta · #10

Pour la méthode, si.
La première personne doit bien ouvrir tous les coffres, regarder quel est le plus long cycle en 2, comme l'a expliqué gwen27 dans son exemple.
La seconde est donc sûre de trouver le coffre en 50 essais au plus, en commençant par le coffre N puis en suivant le cycle.

Le calcul est plus penible.
Il y a 100! arrangements, ça fait beaucoup. On peut les regrouper en "partitions" (ensemble d'entiers dont la somme fait 100, correspondant à tous les arrangements ayant pour longueur de cycle le même ensemble d'entiers). Sauf que pour 100, il y en a 109 millions et des poussières différents...

Au final, je n'ai pas trouvé mieux que de coder ça. Au final, il faut ouvrir en moyenne 28.95 coffres, contre 50.5 sans permutation (logique)
Et de la même manière j'ai aussi la moyenne des plus grandes longueurs de cycle : 35.19

Je ne donne pas la formule de calcul ni le code, ça permettra de ne pas polluer les réflexions de ceux qui pourraient trouver une règle générale

enigmatus · #11

Bonsoir scarta,
Je n'avais pas trouvé comment améliorer le tirage en permutant le contenu de 2 coffres, mais je me suis attaqué aux probabilités.

Je suppose au départ une permutation aléatoire des contenus, et une valeur X également aléatoire.
Pour le pire des cas, la permutation est aléatoire et je suppose que je tombe dans la boucle la plus longue.

Voici ce que j'obtiens pour 10 coffres, en 20 secondes environ :

Code:

Sans optimisation :
nb moyen de coffres à ouvrir = 13/4 = 3.250000
nb moyen dans le pire des cas = 23759791/3628800 = 6.547561

Avec optimisation :
nb moyen de coffres à ouvrir = 75781001/36288000 = 2.088321
nb moyen dans le pire des cas = 1382077/362880 = 3.808634

Je n'ai pas l'impression que ça concorde avec tes résultats. Pourrais-tu montrer tes valeurs pour 10 coffres ?

nodgim · #12

@ Enigmatus: je ne crois pas que tes résultats soient corrects pour le nb moyen de coffres à ouvrir, tu ne peux pas diviser par 3 par l'inversion d'un coffre. En fait, tu ne peux diviser au mieux que par 2. Les chiffres annoncés par Scarta me semblent plausibles.

enigmatus · #13

@nodgim #12 :
Inverser 2 coffres me fait passer en moyenne de 3.250 à 2.088, et en moyenne dans le pire des cas de 6.548 à 3.809. On divise le nombre d'essais par moins que 2.

nodgim · #14

Pardon Enigmatus, j'ai fait une mauvaise lecture de ton algo.
Pourquoi dans ce cas remets tu en cause les données de Scarta ?
Perso, je ne sais pas trop comment ça évolue, c'est sûr que ça tend vers une limite quand le nombre de coffres augmente, mais laquelle ?

enigmatus · #15

@nodgim #14 :

scarta #10 a écrit:
contre 50.5 sans permutation

C'est juste cette valeur qui me paraît bizarre, à moins que ce ne soit le plus mauvais cas (une seule boucle de 100).
Pour le reste, je ne remets pas en cause son algorithme, et j'aimerais comparer nos valeurs pour 10 coffres.

nodgim · #16

@ Enigmatus: si tu as regardé pour 10 coffres, sans doute aussi pour moins de 10. Tu dois donc trouver une tendance pour la moyenne des coffres à ouvrir.

Le nombre de boucles de 100 coffres est 99!, soit 1% du nombre total des codes possibles.

enigmatus · #17

@nodgim #16 :
J'ai trouvé des erreurs dans mon algorithme, et certains résultats présentés en #11 étaient erronés.
Voici les valeurs corrigées, de 2 à 10 coffres :

Code:

                                       Pire cas
                                    ----------------
                  Sans     Avec     Sans     Avec
                  échange  échange  échange  échange

  2 coffres =>    1.500    1.000    1.500    1.000
  3 coffres =>    2.000    1.222    2.167    1.333
  4 coffres =>    2.500    1.479    2.792    1.708
  5 coffres =>    3.000    1.770    3.425    2.108
  6 coffres =>    3.500    2.047    4.043    2.400
  7 coffres =>    4.000    2.329    4.675    2.787
  8 coffres =>    4.500    2.609    5.296    3.103
  9 coffres =>    5.000    2.894    5.925    3.475
 10 coffres =>    5.500    3.177    6.548    3.809

nodgim · #18

Merci Enigmatus.
Pour la 1ère colonne, ça confirme donc le résultat de Scarta, puisque le nombre moyen de coffres à ouvrir est (n+1)/2, formule qui reste à prouver.

scarta · #19

Pour la moyenne avec échange , de tête je me rappelle le résultat du 5 (qui tombe pile: 1.77)
Sans permutation, le résultat est bien (n+1)/2, prouvé en une seule ligne: les n coffres sont équiprobables, l'espérance vaut donc n(n+1)/2/n = (n+1)/2

C'est la que c'est intéressant en fait. Sans permutation, ça revient à ouvrir les coffres au pif. Ceux qui pensent le contraire sont, en général, ce qui sont sûrs de pouvoir faire fortune au casino et qui repartent fauchés.

Pour le cas avec permutation, il faut sommer, pour chaque partition de N, le produit "nb d'occurences de la partition" x "somme des carrés des longueurs de cycles après permutation"
On divise ensuite le tout par n.n!

Le nombre d'occurences d'une partition {a_k,l_k}, où l_k sont les longueurs de chaînes et a_k le nombre de fois où cette longueur est utilisée, est :
n!/produit(l_k)/produit(a_k!)
Je vous laisse le trouver si vous voulez

Pour n=5 par exemple, sans permutation
5 ==> 5!/5 * 25 = 600
4-1 ==> 5!/4 * (16+1) = 510
3-2 ==> 5!/6 * (9+4) = 260
3-1-1 ==> 5!/3/2 * (9+1+1) = 220
2-2-1 ==> 5!/4/2 * (4+4+1) = 135
2-1-1-1 ==> 5!/2/6 * (4+1+1+1) = 70
1-1-1-1-1 ==> 5!/5! * (1+1+1+1+1) = 5
Total: 1800, divisé par 5.5!=600, ça fait 3
Ça valide donc bien le résultat (n+1)/2

Pareil, avec permutation (ça change la somme des carrés)
5 ==> 5!/5 * (9+4) = 312
4-1 ==> 5!/4 * (4+4+1) = 270
3-2 ==> 5!/6 * (4+4+1) = 180
3-1-1 ==> 5!/3/2 * (4+1+1+1) = 140
2-2-1 ==> 5!/4/2 * (4+1+1+1) = 105
2-1-1-1 ==> 5!/2/6 * (1+1+1+1+1) = 50
1-1-1-1-1 ==> 5!/5! * (1+1+1+1+1) = 5
Total: 1062/600, soit 1.77 tout pile

En mémorisant les factorielles, on peut itérer recursivement sur les différentes partitions. Mais comme le nombre de partition d'un entier croit plutôt vite, je doute qu'on puisse aller beaucoup plus loin que 100...

enigmatus · #20

Pour 5 coffres, j'obtiens bien les mêmes valeurs que scarta en #19.
Après amélioration de mon script, le résultat pour 50 coffres est obtenu en un peu plus de 3 minutes :

Code:

                                       Pire cas
                                    ----------------
                  Sans     Avec     Sans     Avec
                  échange  échange  échange  échange
 50 coffres =>    25.500   14.624   31.527   17.756

Édité :
Et 18 minutes 30 secondes pour 60 coffres :

Code:

 60 coffres =>    30.500   17.490   37.771   21.242

nodgim · #21

@Scarta: j'avais bien retrouvé l'évident (n+1)/2 après coup, et ai adopté le même mode de calcul à la main, avec cette somme de carrés.

Maintenant, avec ton algo, peux tu exhiber une limite du ratio (nb de coffres à ouvrir après permut) / (nb de coffres à ouvrir avant) ?

Cette limite existe forcément.

scarta · #22

Le problème, c'est que ça risque d'être coton à calculer.
On peut toujours faire tourner le script pour voir comment ça converge, mais mon bout de code ne permet pas de réutiliser les résultats calculés pour n à l'étape n+1
Du coup, même s'il est sensiblement plus rapide que celui d'enigmatus (6s pour calculer n=60), les dernières étapes risquent d'être assez longues...
Et pour l'instant, c'est calculé en valeur exacte (je fais la division tout à la fin, mais c'est des entiers de taille non contrainte sur tout le long): il faudrait que j'essaye avec des doubles, moins précis mais plus rapide peut-être ?

scarta · #23

nodgim a écrit:
Cette limite existe forcément.

Je tiens à dire que je désapprouve le forcément.
Ce ratio pourrait avoir une croissance logarithmique très faible et ne pas converger du tout.

Là pour l'instant, je sors "n"/"moyenne du nombre de coffres à ouvrir après permutation" (de toutes façons le nb de coffre à ouvrir avant est (n+1)/2 donc ça change pas des masses...)
Et graphiquement, je serais bien embêté de dire si c'est convergent ou pas, pour l'instant.
Comme je le disais, mon code reprend tout à 0 après chaque taille n, et chaque itération prend plus de 30 minutes maintenant, donc je doute avoir beaucoup de nouveaux points significatifs prochainement...
Résultat graphique

scarta · #24

Bon, j'ai tout réécrit pour encore optimiser un peu (en C cette fois, avec libgmp pour les grands entiers)
Le code

Code:

#include <sys/time.h>
#include <time.h>
#include <stdlib.h>
#include <stdio.h>
#include <gmp.h>

typedef struct timeval timer;
mpz_t *factorial;
int max_size = 500;
int size;

void compute(mpz_t res, int remaining_size, int max, int* stack, int stack_index)
{
    if(remaining_size == 0 || max == 1)
    {
        for(int i=0; i<remaining_size; i++)
            stack[stack_index + i] = 1;
        mpz_t local_res, partition_count;
        mpz_init_set_si(local_res, 1+(stack[0] * stack[0] - 1) / 2);
        mpz_init_set(partition_count, factorial[size]);
        for(int i=0; i<stack_index + remaining_size && stack[i] != 1; i++)
            mpz_cdiv_q_ui(partition_count,partition_count,stack[i]);
        int same_length_cycle_count = 1;
        for(int i=1; i<stack_index + remaining_size; i++)
        {
            mpz_add_ui(local_res, local_res, stack[i]*stack[i]);
            if(stack[i] == stack[i-1])
                same_length_cycle_count++;
            else
            {
                mpz_cdiv_q(partition_count, partition_count, factorial[same_length_cycle_count]);
                same_length_cycle_count = 1;
            }
        }
        mpz_cdiv_q(partition_count, partition_count, factorial[same_length_cycle_count]);
        mpz_addmul(res, partition_count, local_res);
        mpz_clear(partition_count);
        mpz_clear(local_res);
        return;
    }
    for(int cycle_length = max > remaining_size ? remaining_size : max; cycle_length >= 1; cycle_length --)
    {
        stack[stack_index] = cycle_length;
        compute(res, remaining_size - cycle_length, cycle_length, stack, stack_index + 1);
    }
}

int main(int argc, char *argv[])
{
    factorial = malloc((max_size+1)*sizeof(mpz_t));
    mpz_init_set_si(factorial[0],1);
    double s;

    for(int i=1; i<=max_size; i++)
    {
        mpz_init(factorial[i]);
        mpz_mul_si(factorial[i], factorial[i-1], i);
    }

    for(size = 2; size <= max_size; size++)
    {
        timer start;
        gettimeofday(&start, NULL);
        mpz_t numerator, compute_result;
        
        mpz_init(compute_result);
        mpz_init_set_si(numerator, size*size);
        
        mpz_mul(numerator, numerator, factorial[size]);
        mpz_mul_ui(numerator, numerator, 1000000);
        
        int* array = malloc(sizeof(int)*size);
        compute(compute_result, size, size, array, 0);
        
        timer stop;
        gettimeofday(&stop, NULL);
        s=difftime(stop.tv_sec, start.tv_sec) + ((double)stop.tv_usec - (double)start.tv_usec)/1000000.0;
        
        mpz_cdiv_q(numerator, numerator, compute_result);
        
        printf("%d\t%s\t(%.5fsec)\n", size, mpz_get_str(NULL, 10, numerator), s);
        
        mpz_clear(compute_result);
        mpz_clear(numerator);
    }
}

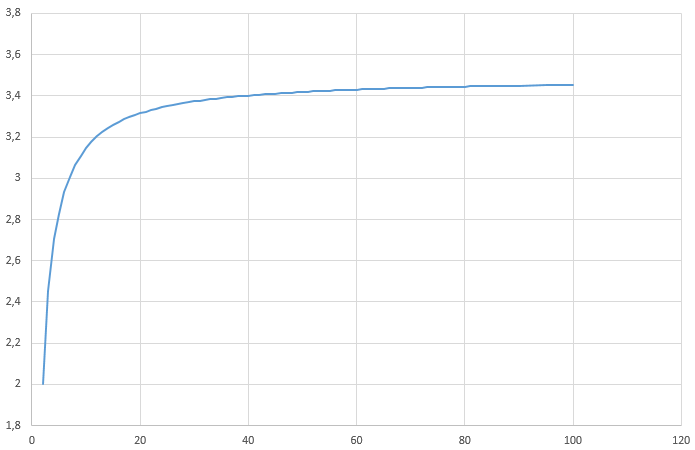
Les résultats

Code:

2    2000000    (0.00032sec)
3    2454546    (0.00000sec)
4    2704226    (0.00000sec)
5    2824859    (0.00001sec)
6    2931464    (0.00001sec)
7    3005770    (0.00001sec)
8    3066240    (0.00001sec)
9    3109529    (0.00001sec)
10    3147978    (0.00002sec)
11    3177389    (0.00002sec)
12    3203466    (0.00003sec)
13    3224175    (0.00004sec)
14    3243165    (0.00006sec)
15    3258971    (0.00008sec)
16    3273472    (0.00011sec)
17    3285569    (0.00013sec)
18    3296934    (0.00019sec)
19    3306748    (0.00026sec)
20    3315903    (0.00032sec)
21    3323859    (0.00041sec)
22    3331411    (0.00054sec)
23    3338073    (0.00071sec)
24    3344388    (0.00088sec)
25    3350003    (0.00070sec)
26    3355366    (0.00139sec)
27    3360199    (0.00391sec)
28    3364818    (0.01100sec)
29    3368984    (0.00809sec)
30    3372995    (0.00328sec)
31    3376657    (0.00848sec)
32    3380174    (0.01561sec)
33    3383394    (0.00626sec)
34    3386507    (0.01293sec)
35    3389374    (0.02011sec)
36    3392145    (0.03047sec)
37    3394705    (0.03608sec)
38    3397188    (0.04315sec)
39    3399497    (0.04983sec)
40    3401736    (0.06640sec)
41    3403819    (0.07488sec)
42    3405847    (0.08422sec)
43    3407746    (0.11873sec)
44    3409591    (0.15425sec)
45    3411321    (0.19212sec)
46    3413008    (0.18688sec)
47    3414595    (0.21655sec)
48    3416143    (0.24483sec)
49    3417602    (0.29722sec)
50    3419027    (0.42788sec)
51    3420375    (0.34802sec)
52    3421692    (0.39035sec)
53    3422938    (0.49760sec)
54    3424159    (0.54944sec)
55    3425317    (0.61576sec)
56    3426451    (0.69368sec)
57    3427528    (0.78667sec)
58    3428585    (0.89454sec)
59    3429591    (1.04672sec)
60    3430578    (1.13582sec)
61    3431518    (1.44800sec)
62    3432442    (1.66220sec)
63    3433324    (1.95147sec)
64    3434190    (2.16669sec)
65    3435018    (2.64504sec)

Je vais laisser tourner toute la nuit, on verra bien demain

scarta · #25

Les résultats suivants
66 3435832 (2.89729sec)
67 3436612 (3.37375sec)
68 3437379 (3.87795sec)
69 3438114 (4.51573sec)
70 3438837 (5.15969sec)
71 3439531 (6.38357sec)
72 3440214 (7.33236sec)
73 3440871 (8.40440sec)
74 3441517 (9.41990sec)
75 3442139 (11.29256sec)
76 3442752 (12.79537sec)
77 3443342 (14.63209sec)
78 3443923 (16.66970sec)
79 3444484 (19.57218sec)
80 3445037 (22.23323sec)
81 3445570 (25.78765sec)
82 3446096 (29.62653sec)
83 3446603 (34.53361sec)
84 3447104 (39.46415sec)
85 3447588 (53.91956sec)
86 3448066 (55.99537sec)
87 3448528 (63.54074sec)
88 3448984 (72.56975sec)
89 3449426 (82.99825sec)
90 3449862 (95.02699sec)
91 3450284 (108.36027sec)
92 3450701 (124.85596sec)
93 3451105 (143.49297sec)
94 3451505 (165.11290sec)
95 3451892 (190.05570sec)
96 3452275 (215.39312sec)
97 3452647 (245.31375sec)
98 3453014 (321.18667sec)
99 3453371 (315.29751sec)
100 3453723 (363.69596sec)
101 3454066 (414.90384sec)
102 3454405 (471.83509sec)
103 3454735 (545.55016sec)
104 3455061 (619.08741sec)
105 3455378 (699.74846sec)
106 3455691 (791.70062sec)
107 3455997 (893.68834sec)
108 3456299 (1025.08472sec)
109 3456593 (1141.01855sec)
110 3456884 (1289.56628sec)
111 3457168 (1471.71688sec)
112 3457449 (1668.62292sec)
113 3457723 (1907.62177sec)
114 3457994 (2149.19385sec)
115 3458258 (3624.31828sec)
116 3458520 (2747.65911sec)
117 3458775 (3077.22442sec)
118 3459028 (3461.87625sec)
119 3459275 (3912.87264sec)
120 3459519 (4408.41504sec)
121 3459758 (6244.78433sec)
122 3459994 (5633.33250sec)

La nouvelle version graphique, avec en orange une courbe basée sur ln(ln(ln(ln(x)))) (avec quelques multiplicateurs). Pas sûr à 100% que ça converge...
Mais bon, l'écart commence (de manière à peine perceptible) à s'agrandir passée la barre des 100, donc je pense que ça converge au final

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 21-10-2017 22:54:58

100 codfres (logique et probas)

#0 Pub

#2 - 22-10-2017 14:23:51

100 coffres (logiqeu et probas)

Code:

Code:

Code:

#3 - 23-10-2017 15:42:46

100 coffres (logiqu eet probas)

#4 - 23-10-2017 15:57:16

100 coffers (logique et probas)

#5 - 23-10-2017 20:35:06

100 coffrse (logique et probas)

#6 - 24-10-2017 06:01:30

100 coffres (olgique et probas)

#7 - 26-10-2017 16:37:09

010 coffres (logique et probas)

#8 - 26-10-2017 17:49:08

100 coffres (logiquee et probas)

#9 - 26-10-2017 22:29:41

100 coffres (ligique et probas)

#10 - 27-10-2017 07:55:08

100 ccoffres (logique et probas)

#11 - 27-10-2017 22:34:38

100 coffres (logique et probass)

Code:

#12 - 28-10-2017 08:00:22

100 coffres (logiquue et probas)

#13 - 28-10-2017 08:54:14

100 coffres (logique et probas))

#14 - 28-10-2017 09:58:19

100 coffres (loggique et probas)

#15 - 28-10-2017 10:31:31

100 coffres (logique et probbas)

scarta #10 a écrit:

#16 - 28-10-2017 14:45:26

100 cofdres (logique et probas)

#17 - 28-10-2017 17:11:01

100 coffres (logiqie et probas)

Code:

#18 - 28-10-2017 18:14:19

100 coffres (logique et ptobas)

#19 - 28-10-2017 22:00:24

100 coffres (logiqu eet probas)

#20 - 28-10-2017 22:45:55

100 ccoffres (logique et probas)

Code:

Code:

#21 - 29-10-2017 06:54:05

100 coffres (logique et porbas)

#22 - 30-10-2017 09:40:36

100 coffres (kogique et probas)

#23 - 30-10-2017 11:31:49

100 coffres l(ogique et probas)

nodgim a écrit:

#24 - 30-10-2017 16:54:14

100 coffres (logique et pronas)

Code:

Code:

#25 - 31-10-2017 08:28:53

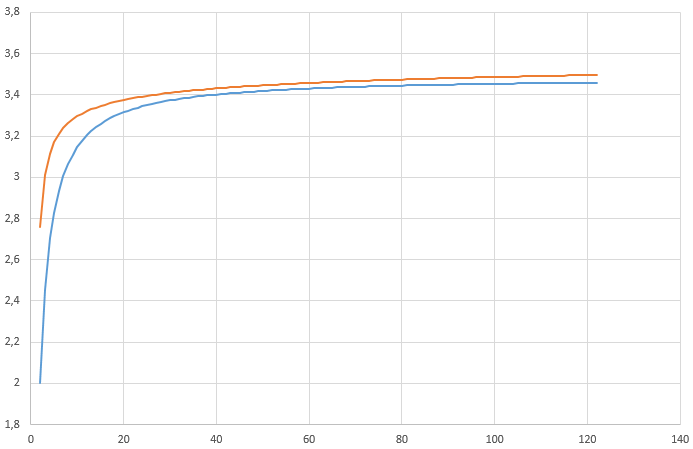
100 coffres (ogique et probas)

Réponse rapide

Sujets similaires

Pied de page des forums