 |
#1 - 05-04-2020 10:23:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
quadrilatère, careé et rectangle
Bonjour @ tous.
On place 1 point au hasard sur chaque coté d'un carré ( pas les sommets). Peut-on toujours inscrire un rectangle à cotés parallèles à ceux du carré dans le quadrilatère reliant les 4 points ?
Bonne réflexion.
#2 - 05-04-2020 15:07:32
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Quadrilatère, carré et rectangl
Non, voici un contre-exemple étudié de manière analytique.
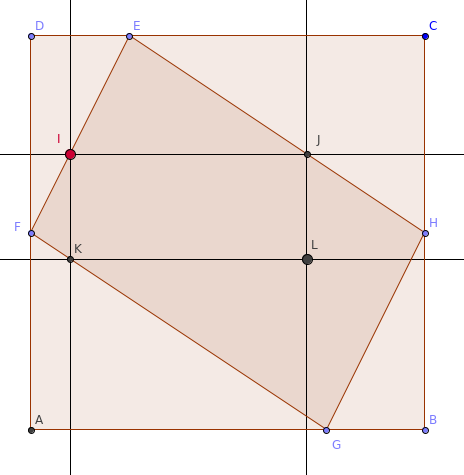
Dans le repère (A,B,D), on a E(1/4;1), F(0;1/2), G(3/4;0), H(1;1/2).
On place I sur [EF] d'abscisse a, alors :
yI=yJ=2a+1/2
yK=yL=1/2-2a/3
xJ=xL=1-3a
Donc L(1-3a;1/2-2a/3), or l'équation de (GH) est y=2x-3/2.
Si on veut que L appartienne à (GH), cela donne 1/2-2a/3 = 2*(1-3a)-3/2 donc a=0 : ce n'est pas possible.
#3 - 05-04-2020 16:25:47
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrilatère,, carré et rectangle
Oui, Ebichu.
Peux-tu trouver une règle générale sur la contrainte du placement des points à respecter pour l'inscription ?
C'est un peu le but de la question.
#4 - 06-04-2020 20:51:19
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
uadrilatère, carré et rectangle
Bonjour Nodgim,
Considérons que notre carré d’origine, de côté 1, est placé dans un repère centré sur un des coins et orienté sur ses côtés. Les quatre points sont placés sur ses cotés successifs : A1 (X1,0) , A2 (0,Y2), A3(X3,1), A4(1,Y4).
Considérons A1 et A2 positionnés. 4 cas
Cas 1 (particulier) : une infinité de solution si X3=X1 et Y4=Y2 (trivial par symétrie)
Cas 2 (particulier): une solution singulière, sans surface, si X3=X1 ET Y4<>Y2 (une droite, en somme). Pareil si Y4=Y2 ET X3<>X1 bien sûr.
Cas 3 (général): une unique solution si X3>X1 ET Y4<Y2, ou si X3<X1 ET Y4>Y2
Cas 4 (général): aucune solution si X3>X1 ET Y4>Y2, ou si X3<X1 ET Y4<Y2
Pour se convaincre du cas 3, on peut raisonner par ‘suite de rebonds’ en partant de A1.
Supposons que X3>X1 (dans le cas contraire, je retourne la figure et revient à cette situation). Donc on a aussi Y4<Y2 par construction du cas 3. Et on va ‘tourner’ dans le sens anti-trigonométrique (1er rebond sur la droite A2A3) car X3>X1.
P0, point de départ, en (XP0, YP0) avec XP0=X1, YP0=0
Donc P1, sur la droite A2A3 est en (X1, YP1), et P2 sur A3A4 est en (XP2, YP1), avec X1<X3<XP2<1
Puis P3, sur la droite A4A1 est en (XP2, YP3), et enfin P4, sur la droite A1A2 est en (XP4, YP4), avec donc 0<XP4<X1 (0<XP4 car Y2<Y4)
Donc 0<XP4<XP0. On peut faire un tour de plus et montrer que 0<XP8<XP4<XP0.
On a une suite strictement décroissante et bornée. Donc convergente. Par exemple en X0 sur A1A2.
On peut ensuite montrer par la même méthode que, si on part d’un P0 tel que XP0<X0, alors XP0<XP4<X0, puis XP4<XP8<X0… la suite est croissante. Donc la solution est unique.
Voilà voilà.
Bon je sais Nodgim, tu vas me dire ‘et les cas 2 et 4 ?’. Et tu as raison. Seulement voilà, si c’est clair graphiquement, il faut sans doute faire un raisonnement par l’absurde en supposant qu’une solution (ou une solution non singulière dans le cas 2) existe. Mais pas eu le temps de trouver le truc. Bon, comme graphiquement c’est clair, j’imagine que ça suffit ? 😉
#5 - 06-04-2020 22:17:41
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Quadrilatère, carrré et rectangle
On place un repère tel que le carré devient le carr unité à la base du repère. On nomme c1 le côté du carré entre (1,0) et (1,1), c2 entre (0,0) et (1,0), c3 entre (0,1) et (1,1) et c4 entre (0,0) et (0,1)
On nomme s1 le sommet du quadrilatère sur c1 (resp s2, s3, s4).
On nomme p12 un point libre sur [s1 s2]
On nomme p13 la projection de p12 sur [s1 s3) parallèlement à c1
p12 et p13 ont donc les mêmes ordonnées
On nomme p24 la projection de p12 sur [s2 s4) parallèlement à c2
On nomme p34 la projection de p13 sur [s3 s4) parallèlement à c2
(quitte à prolonger les axes)
Supposons sans perte de généralité que l'abscisse de s4 est supérieure à celle de s2.
Soit l1 la longueur p12p24 et l2 la longueur p13p34.
Plaçons p12 en s1. On a alors p13 = p12 = s1
On remarque facilement que p24 est dans le carré et p34 hors du carré. (C'est du au choix que l'abscisse de s4 est supérieure à celle de s2). On en déduit que l1 < l2.
Maintenant, si l'ordonnée de s3 est supérieure à celle de s2, plaçons p12 et p13 sur la même ordonnées que celle de s3.
On a alors l2 = 0 < l1
Inversement, si l'ordonnée de s2 est supérieure à celle de s3, plaçons p12 et p13 sur la même ordonnées que celle de s2.
On a alors l1 = 0 < l2
On déplace p12 et p13 continument à partir de s1 sur [s1, s2] et [s1, s3] en gardant ces deux points parallèles par rapport à c1 (leurs ordonnées respectives restent donc égales). On s'arrête lorsque l'ordonnée de p12 et p13 devient égale à la plus grande entre celle de s2 et s3 (autrement, l'un des points sortirait du carré.
La quantité l1 -l2 varie continument et monotonement par rapport au déplacement de p12 et p13.
On a au départ l1 - l2 < 0.
On a à l'arrivée l1 - l2 < 0 si l'ordonnée de s2 est supérieure à celle de s3 et l1 - l2 > 0 si l'ordonnée de s3 est supérieure à celle de s2
D'après le théorème de la bijection, il existe une unique position ou les valeurs l1 et l2 sont égales ssi l'ordonnée de s3 est supérieure à celle de s2
De plus, il est facile de vérifier que si il y a croisement, les quatre sommets du rectangle sont dans le carré.
Dans le cas où l'ordonnée de s3 est supérieure à celle de s2, on voit bien que les longueurs se croisent et qu'on obtient un rectangle à cet instant
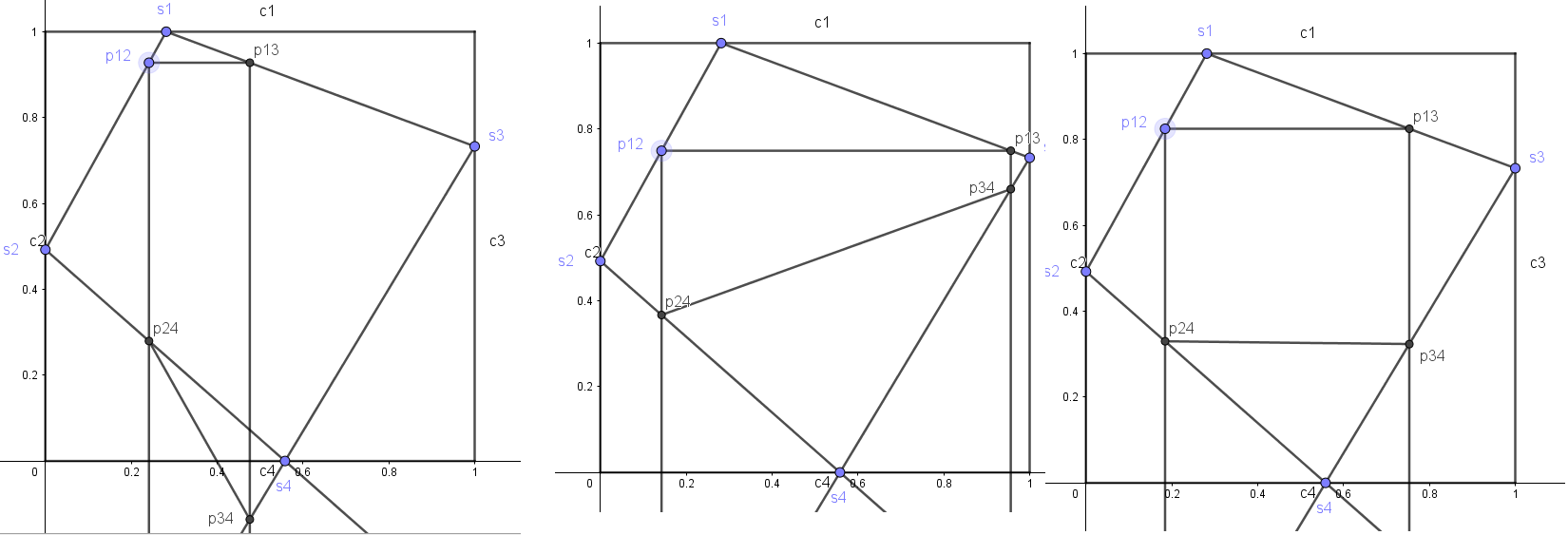
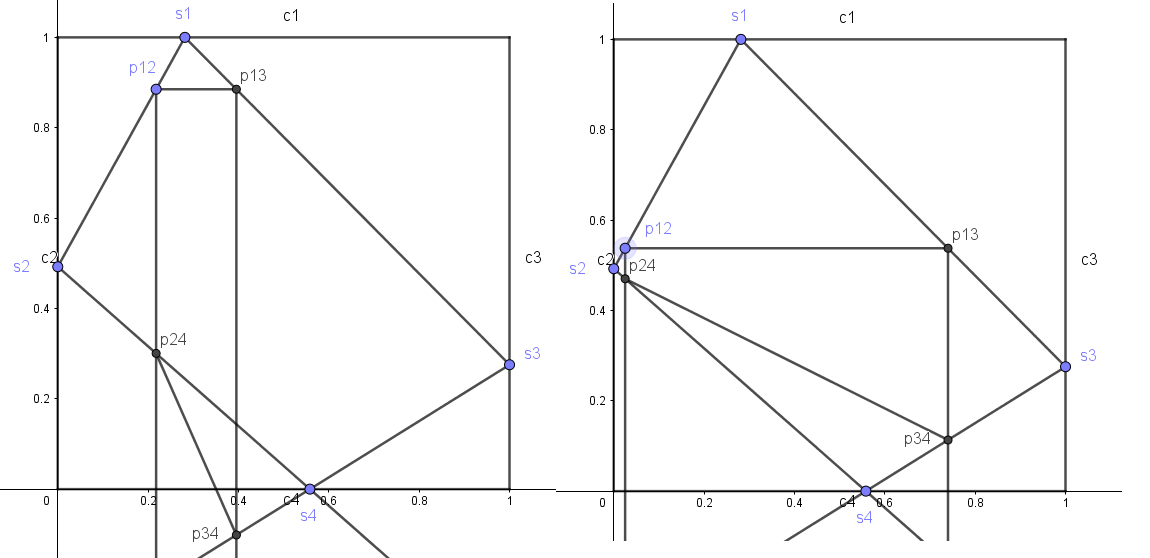
Dans le cas où l'ordonnée de s2 est supérieure à celle de s3, on voit bien que l2 restera toujours supérieure à l1, il n'y aura donc jamais de rectangle...
#6 - 07-04-2020 17:35:06
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrilatère, carré et reectangle
@ Toufau : En effet, ce n'est pas encore percutant comme argument de preuve.
Il faudrait continuer de creuser.
@ Caduk : y a de l'idée je crois, mais oui j'aimerais bien un petit dessin, comme tu le proposes. Je redonne du temps de toute façon, ce n'est pas facile.
Perso, j'ai un argument dit à la Vasimolo, avec ses gâteaux infernaux qui nous manquent un peu. Un argument à la Vasimolo, pour ceux qui ne voient pas ce que je veux dire, est un dessin qui se passe presque de commentaires....
Bon courage.
#7 - 07-04-2020 22:18:47
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Quadrilatère, carré et rectanlge
J'ai édité pour rajouter les images, et j'ai un peu modifié pour clarifier (en tout cas j'espère)
#8 - 08-04-2020 09:33:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrillatère, carré et rectangle
ça me semble correct, caduk. Bravo @ toi !
J'ai une preuve plus courte, mais bon, le but est atteint.
#9 - 08-04-2020 23:20:46
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 644
- Lieu: Ville 2/N près 2*i
Quadrilatère, carré et rcetangle
Coucou,
J'ai peut-être raté qqch dans l'énoncé mais je tombe sur un contre-exemple
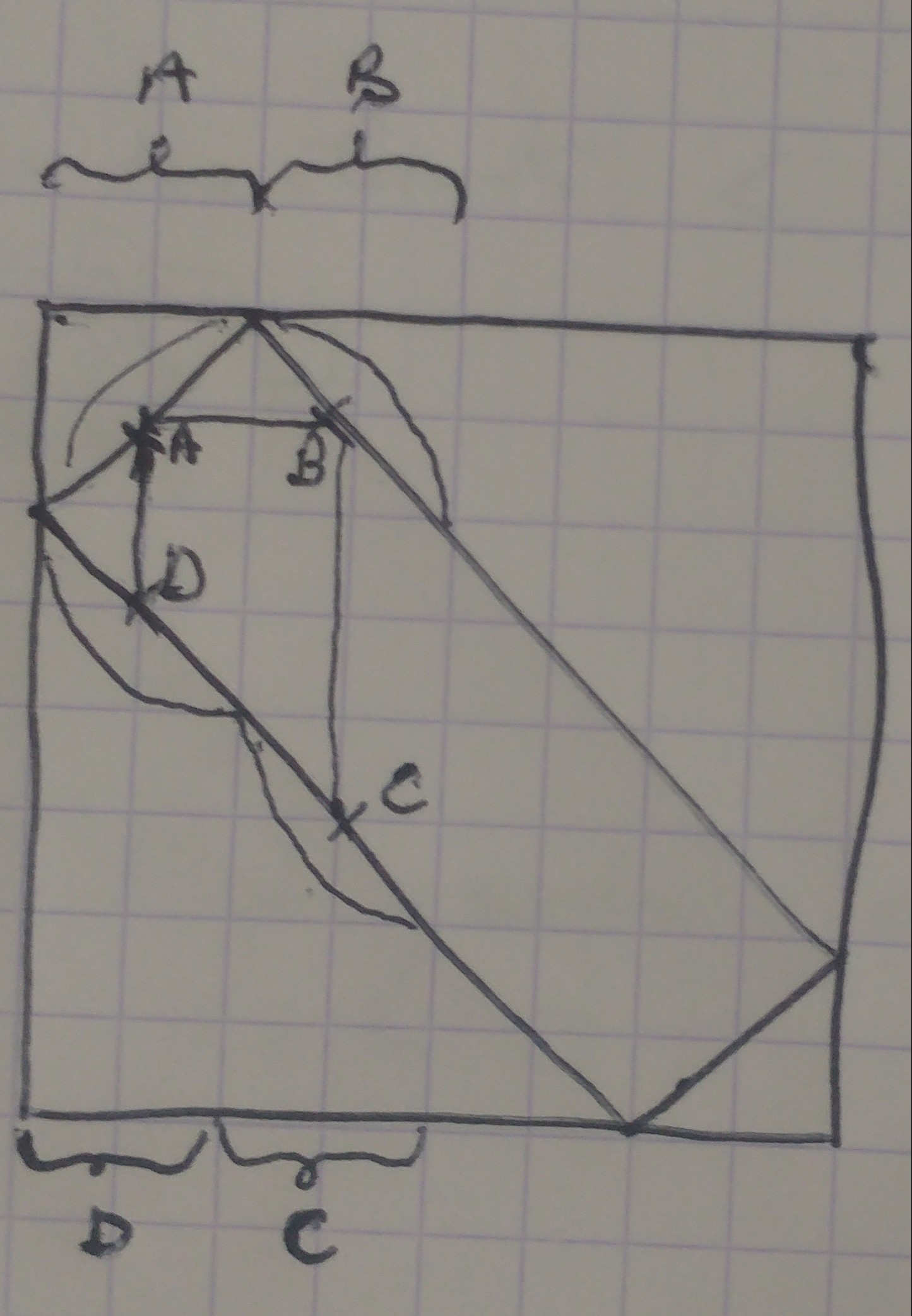
En résumé, si les 4 points choisis sur le carré forment un quadrilatère relativement étroit. Il est impossible d'atteindre le 4e côté en traçant des lignes horizontales et verticales.
#10 - 09-04-2020 08:03:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrilatère ,carré et rectangle
C'est tout à fait juste, Migou, il y a des contre-exemples.
La question sous-jacente est tout de même, maintenant, de se demander s'il existe une règle pour le placement des points telle que certaines configurations accepteront le rectangle et d'autres non.
Par exemple, si les points à droite et à gauche sont à la même hauteur, et ceux en haut et en bas sont à la même abscisse, alors il y a toujours des solutions.
#11 - 09-04-2020 08:56:59
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Quadrilatère, carré ett rectangle
Ci-dessous traduction graphique de mon premier post, et traitement du cas 4, où aucune solution n'existe.

#12 - 09-04-2020 10:40:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
quadrilatère, catré et rectangle
@ Toufau : je ne l'avais pas exprimé clairement lors de ma réponse à ton premier message, ton analyse sur les différents cas est correcte et comprise. Là où ça pêche tout de même encore dans ton second message, c'est une preuve bien propre, bien construite. Tout le monde la voit cette suite convergente, mais il faut la justifier correctement, sinon trouver une autre voie de preuve.
#13 - 09-04-2020 12:15:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Quadrilatrèe, carré et rectangle
Bonjour Nodgim
J'ai une solution construite du rectangle quand les coordonnées des quatre points respectent un certain ordre mais j'ai complètement oublié comment on joint une image sur ce site .
Vasimolo
#14 - 09-04-2020 16:25:03
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
quadrilatère, carré et rectangke
Ah là là, ça va nous manquer si tu ne le donnes pas Vasimolo, le dessin de ton gâteau. Pour moi, ce sera aux cerises et à la crème chantilly, merci. 
#15 - 09-04-2020 16:53:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
quadrilatère, carré et rectanhle
J'ai retrouvé comment faire ( c'est quand même un peu tordu  ) )
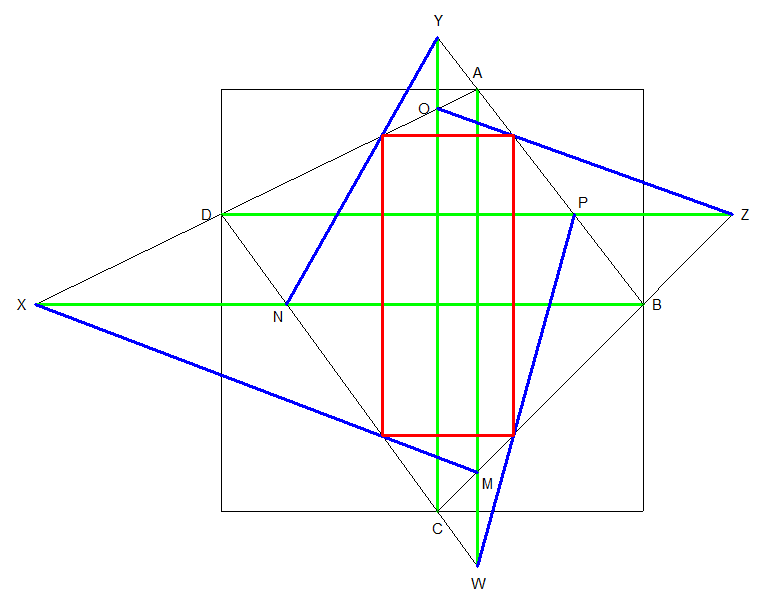
ABCD donné , on place les points W , X , Y , Z puis M , N , O , P . On obtient alors Le rectangle rouge .
La construction ne fonctionne que si W , X , Y et Z sont à l'extérieur des segments [CD] , [AD] , [AB] et [BC] ce qui se traduit aisément en termes de coordonnées dans un repère supporté par les côtés du carré .
Vasimolo
#16 - 10-04-2020 08:18:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrilatère, craré et rectangle
Tiens ! Une construction directe. Voilà bien une troisième solution. Vasimolo, tu ne donnes pas clairement le critère de constructibilité.
Et si, au lieu d'un carré, c'était un rectangle ?
#17 - 10-04-2020 09:19:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Quadrilatère, carré et retangle
La condition me semblait claire : (xC−xA)(yB−yD)>0 .
La construction et les conditions sont les mêmes pour un rectangle .
Vasimolo
#18 - 10-04-2020 09:34:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Quadrilatère, carré et retcangle
Illustration
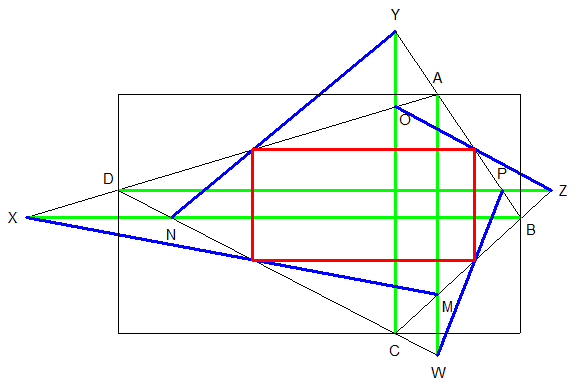
Vasimolo
#19 - 10-04-2020 09:42:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrilatère, carréé et rectangle
Bravo, Vasimolo !
Et la crème Chantilly, alors ?
#20 - 10-04-2020 19:34:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
quadrilatère, carré et rectanfle
Pour la chantilly j'ai du mal à m'approvisionner en ce moment mais je peux apporter un petit plus à ton problème . On peut vérifier par un système de coordonnées que rouge est bien un rectangle . En fait il suffit de vérifier que les côtés opposés du quadrilatère rouge sont parallèles à ceux du rectangle initial . C'est loin d'être beau mais ça montre que le problème est affine c'est à dire qu'on peut poser la même question pour un parallélogramme parallèle à un parallélogramme initial et avec la même réponse .
On doit pouvoir se passer des coordonnées mais ce n'est pas évident à priori .
Vasimolo
#21 - 10-04-2020 22:45:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Quadrilatère, carré et rectanglle
Voici une proposition de solution, mais j'imagine qu'il y a plus élégant. Dans chaque cas, je pars d'un point I situé sur le côté supérieur droit du quadrilatère, puis je trace une horizontale, une verticale, une horizontale, et je regarde si le quadrilatère inscrit obtenu est un rectangle.
Premier cas : si les points sur le carré sont "en face", quelle que soit la position de I, on obtient un rectangle. Ceci se démontre avec le théorème de Thalès utilisé trois fois : a1/b1 = a2/b2 = a3/b3 = a4/b4.
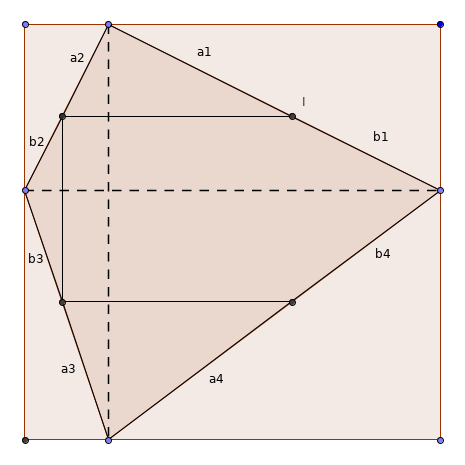
Deuxième cas : si les points en haut et en bas du quadrilatère sont "en face", mais que le point de gauche est plus haut que le point de droite, alors a1/b1 < a2/b2 = a3/b3 < a4/b4 donc comme a1/b1 est différent de a4/b4, le 4e point du quadrilatère inscrit n'est pas en face de I. On ne peut pas former de rectangle inscrit. D'une manière générale, il se passe la même chose dès lors que deux points sont en face, et pas les deux autres.
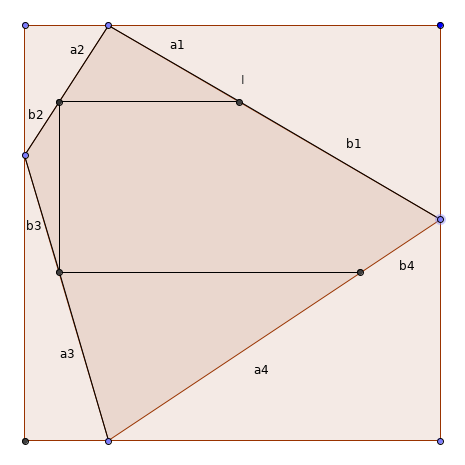
Troisième cas : si le point du haut est à gauche du point du bas, et le point de gauche est plus haut que le point de droite, alors a1/b1 < a2/b2 < a3/b3 < a4/b4, donc le 4e point du quadrilatère inscrit n'est pas en face de I, sinon on aurait a1/b1 > a4/b4. On ne peut pas former de rectangle inscrit. D'une manière générale, il se passe la même chose dès lors l'angle orienté formé par la verticale et la droite passant par les points du haut et du bas est de signe opposé à l'angle orienté formé par l'horizontale et la droite passant par les points de gauche et de droite.
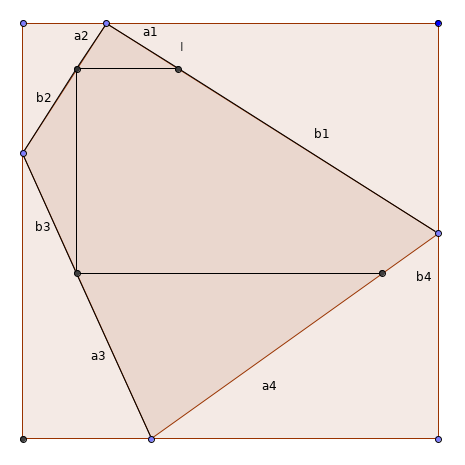
Quatrième cas : l'angle orienté formé par la verticale et la droite passant par les points du haut et du bas est de même signe que l'angle orienté formé par l'horizontale et la droite passant par les points de gauche et de droite. Entre les deux situations extrêmes illustrées sur les 2 figures ci-dessous, où le point I est une fois à droite, et une fois à gauche du 4e point, il existe une situation intermédiaire où les deux points sont en face, et où le quadrilatère inscrit est un rectangle.
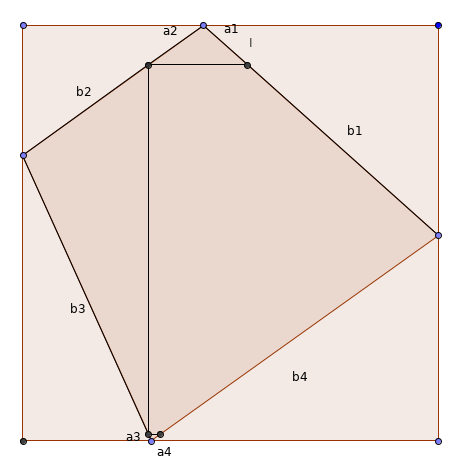
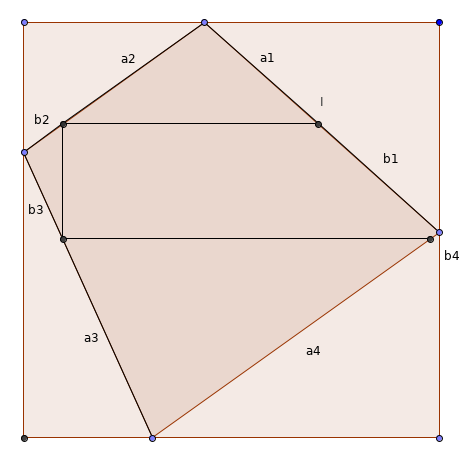
#22 - 11-04-2020 09:34:55
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Quadrilatère, carré t rectangle
@ Ebichu : ce n'est pas mal du tout, j'en était arrivé au même point à un moment donné. Cela cependant ne me satisfaisait pas vraiment, trop de cas en jeu. Ton quatrième cas est une vraie rupture de raisonnement par rapport aux autres cas. Curieusement, j'avais trouvé plus facilement la preuve du rectangle possible, toi tu as bien géré les cas impossibles. Sinon, c'est correct.
L'idéal serait maintenant de trouver, si possible, une preuve plus synthétique.
NB :
@ tous
Je ne dois pas être le seul à avoir tenté un essai d'analyse pure, avec 4 équations de droite, mais si on arrive bien à trouver un résultat, c'est pratiquement impossible d'en déduire les cas possibles et les cas impossibles.
#23 - 11-04-2020 11:45:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Quadirlatère, carré et rectangle
@Nodgim
Le problème avec ces longs dialogues en aveugle , c'est qu'on a la vision des autres uniquement à travers le filtre de celui qui a posé le problème .
Il y a pas mal de choses dans l'exercice qui masquent le fond du problème . Globalement on a deux directions de droites et un quadrilatère dans lequel on veut inscrire un parallélogramme dont les côtés suivent ces directions .
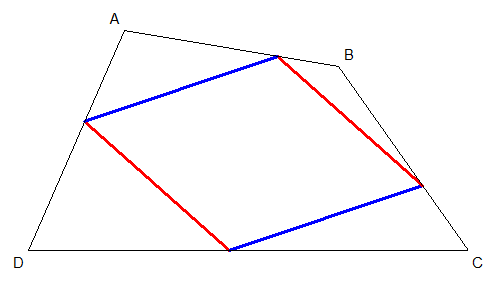
Je ne suis pas allé voir plus loin mais on voit tout de suite les limites de la construction et qu'avec quelques transformations bien senties , elle risque de tomber toute seule .
Vasimolo
#24 - 11-04-2020 16:31:36
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Quadrilatre, carré et rectangle
Oui, je m'attendais à cette réponse 
#25 - 11-04-2020 17:54:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Quadrilatère, crré et rectangle
J'ai une construction simple du parallélogramme :
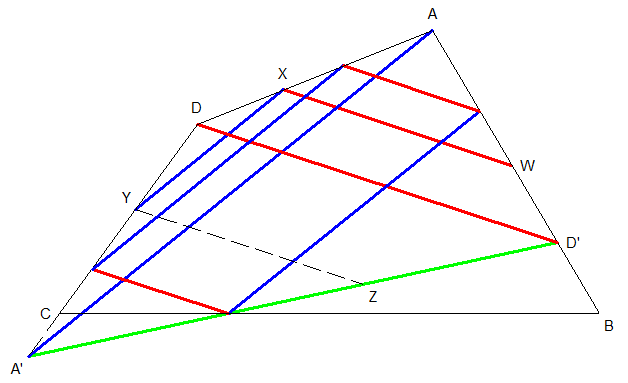
ABCD est le quadrilatère dont les sommets sont sur les côtés d'un parallélogramme aux directions rouges et bleues . Quand le point W décrit la droite (AB) , le quatrième sommet du parallélogramme WXYZ décrit la droite (A'D') en vert . Il n'y a plus qu'à choisir Z sur [BC] pour obtenir la solution .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum




















