@ Vasimolo : dans l'une des pistes que j'avais suivies, il était aussi question de parallélogramme, mais c'était seulement pour montrer l'impossibilité de construction du rectangle. J'avais une autre preuve pour la constructibilité.

Ta réponse est un peu légère Nodgim :"moi aussi j'ai essayé les parallélogrammes" , et le saut à l'élastique , non

Le problème est clairement affine , donc parallélogrammes , rectangles ou carrés , c'est la même approche . Si on demande simplement que la figure à construire ait ses sommets sur les côtés prolongés du quadrilatère , la solution existe et est unique . Après il reste à trouver les conditions pour que la figure reste à l'intérieur du rectangle/parallélogramme initial et la réponse est clairement établie même s'il manque peut-être une preuve formelle .




Vasimolo

Bon le temps est écoulé.

Je donne ma propre solution, qui est donc la 4ème, les 3 autres étant validées.

----------------------------------

On peut considérer la figure comme l’association de 2 systèmes : Les 2 cotés gauche du quadrilatère et son sommet ( le point placé sur le coté gauche du carré ) d’une part, son homologue à droite d’autre part. On suppose que le sommet du système de gauche est plus haut que son homologue de droite. Si l’on fait glisser horizontalement le système de gauche vers la droite, alors la droite qui passe par les 2 intersections des systèmes pivote dans le sens contraire des aiguilles d’une montre pour finir par une pente nécessairement négative. Or, si,dans ce pivotement, l’on passe par la verticale, celle-ci est assimilable au rectangle que l’on cherche. Donc, si au départ la pente de cette droite est déjà négative, on ne passera pas par la verticale et pas de rectangle possible.

Même raisonnement si le sommet de gauche est moins haut que le sommet de droite ( pivotement inverse dans ce cas).

En résumé, si les pentes des diagonales du quadrilatère au départ sont de même signe : pas de rectangle possible. Si les pentes sont de signe contraire, rectangle possible.

Si les sommets sont à la même hauteur : rectangle dégénéré en 1 ligne ( pas de pivotement ). Si en plus la droite est verticale au départ, infinité de rectangles possibles.

NB1 : le pivotement de la droite est exactement identique si on déplace le système de gauche vers le haut ( sommet du système au dessus de son homologue ) ou vers le bas ( sommet en dessous de son homologue). Cette assimilation permet de mieux visualiser le pivotement. 

NB2 : si, au lieu d’un carré comme base de la figure, on choisit un rectangle, le résultat est identique.

@ Caduk: rassure-toi...moi non plus, je ne sais pas le justifier complètement.

Il a dit qu'il l'avait retrouvé, il connaissait donc depuis longtemps.

En effet je ne connaissais pas le problème

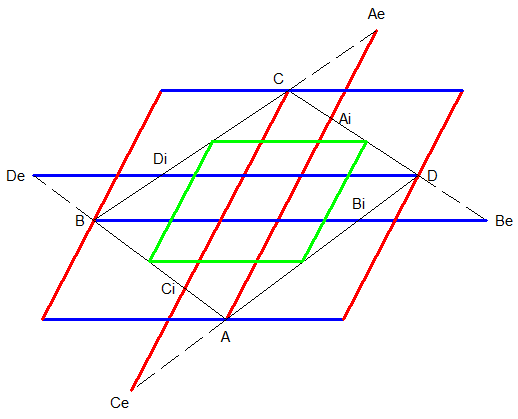
La construction n'est pas si mystérieuse que ça , en fait j'en ai donné deux . La première est un peu tordue car je me suis laissé entraîner par les angles droits qui ne servent vraiment à rien dans le problème . La deuxième construction est assez facile à imaginer si on considère les droites à la place des segments , j'en ai donné le schéma dans le message #25 . On promène un point X sur le côté (AD) du quadrilatère , on place ensuite les points W et Y sur (AB) et (CD) de façon à ce que (XW) et (XY) suivent les directions données par les côtés du parallélogramme . On termine le parallélogramme WXYZ et Z décrit une droite qui vient couper (BC) là où l'on veut .

La construction fonctionne quelles que soient les positions des points A , B , C , et D mais les points W , X , Y et Z ne sont pas forcément à l'intérieur des côtés .

Vasimolo