|
#1 - 08-07-2011 11:08:40
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
dissection de recrangle
Hello p2tétiens et p2tétiennes! (d'ailleurs il y a des p2tétiennes? :p je rigole).
J'ai de quoi vous faire griffonner ce weekend!
Seriez vous capable de me découper savamment un rectangle (celui que vous voulez) uniquement en plusieurs carrés tous de tailles différentes?
Bonne chance.
(Faire la même chose avec un carré est réservé aux grandes personnes, mais le cas du rectangle est tout à fait abordable)
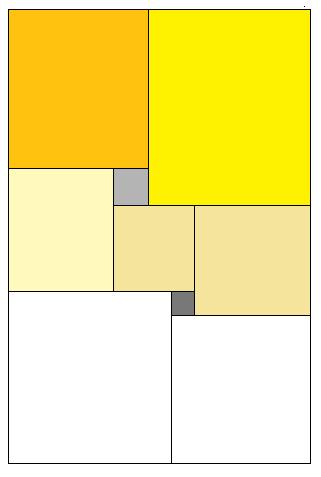
SOLUTION:
Spoiler : [Afficher le message] La partie intéressante du problème est de trouver comment l'aborder.
L'astuce consiste dans un premier temps à faire une sorte de croquis imparfait, vous partez d'un dessins de rectangle et vous le remplissez "au pif" avec des carrés en tentant d'arriver le plus vite possible à le remplir et sans dessiner quelque chose qui implique des carrés de même taille (par exemple il est évident que si vous joignez deux carrés par un bord ils sont de même taille). Une fois votre croquis imparfait achevez (ou si vous préférez votre pavage avec des rectangles que vous déclarez être des carrés) il est temps de vérifier qu'il est valable et pour ceci il suffit de résoudre les quelques équations très simple que votre croquis pose. Si vous posez naïvement le système vous tomberez généralement sur un système avec autant d'inconnues que de carrés mais facile à résoudre et wolfram peut vous aider, plutôt que de poser naïvement le système il est généralement possible d'exprimer de proche en proche la taille de chaque carré en tant que combinaison linéaire de deux carrés judicieusement choisis ce qui ne fait donc que deux inconnues.
Il y a deux solutions à ce problème faisant intervenir 9 carrés (le minimum)
Voir #12 de FRIZMOUT
Pour la méthodologie détaillée voir #13 de looozer
PS: Pour la culture la version "pour adultes" avec un carré fait intervenir au minimum 21 carrés ^^ pour plus d'information sur le sujet "squaring the square" "perfect square" "squared square" etc...
http://mathworld.wolfram.com/PerfectSqu … ction.html
Merci à tous les participants.
#2 - 08-07-2011 12:02:22
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Dissection d erectangle
C'est chaud, je viens de m'y frotter un peu, et le fait q'il y ait une réponse m'intrigue...
Bon, déjà, le plus petit des carrés ne peut pas être dans un angle du rectangle ni sur un bord, ça c'est sûr, mais après... 
Bon, je continue de chercher ! 
#3 - 09-07-2011 01:56:05
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Dissection de rcetangle
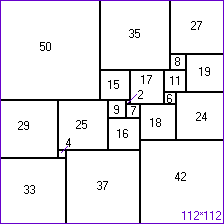
Le carré c'est facile 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#4 - 09-07-2011 08:44:22
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Dissection dde rectangle
1. rectangle 176x177
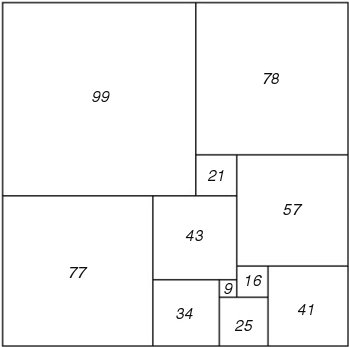
2. carré
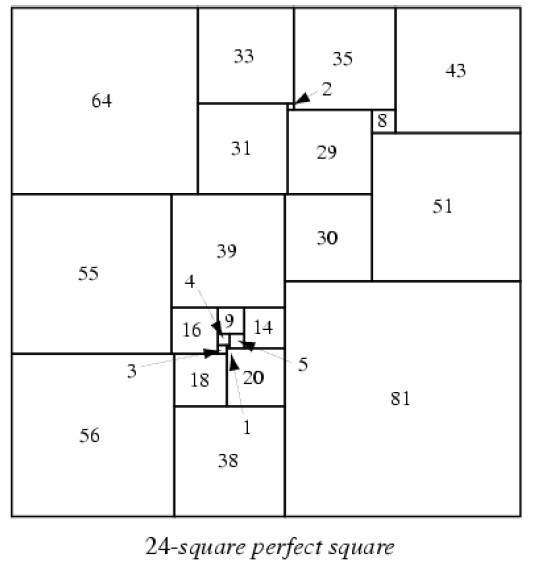
#5 - 09-07-2011 10:19:19
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
didsection de rectangle
@halloduda: Ce ne sont même pas les solutions minimales que tu as trouvé sur le net (Je n'aurais pas posé le problème s'il n'y avait pas plus simple pour le rectangle) c'est intéressant à chercher autrement qu'avec google faut trouver la méthodologie c'est le meilleur moment dans un problème trouver comment l'aborder ^^
#6 - 09-07-2011 11:10:12
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
dissection dz rectangle
@nodgim: Si ça t'aide tu peux faire toutes les assomptions que tu veux sur les rapports de longueur mais je n'ai rien précisé tu es totalement libre.
#7 - 09-07-2011 11:23:57
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,097E+3
dossection de rectangle
Déjà, je verrai bien un truc du genre :
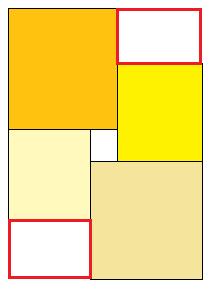
Mais les deux rouges sont des rectangles. Le carré "imbriqué" est bien pratique pour des dimensions différentes.
Il faut en mettre d'autres ? Parce que ça va faire un paquet de carrés à force !
#8 - 09-07-2011 11:34:04
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
dissection dr rectangle
@Gwen27: Spoiler : [Afficher le message] Tu es sur la bonne voie, la bonne méthodologie, même si tes carrés rouge pouvait être carré on voit qu'ils seraient de la même taille que leur voisin (car collé par un bord) donc continue à construire un croquis en faisant en sorte que a n'arrive pas ^^ (et oui il en faut des carré un certain nombre mais avec méthode on peut trouver (j'ai trouvé)
#9 - 09-07-2011 11:48:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,097E+3
#10 - 09-07-2011 14:41:07
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,097E+3
dissection fe rectangle
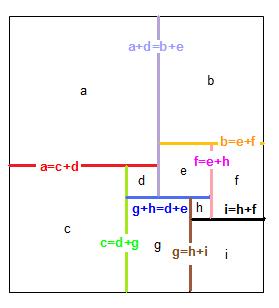
Fait suer, wolfram aide un peu :

Grrrrr .... g=b i=d, on oublie wolfram.... Ou ma solution amène à des carrés de même taille !
#11 - 09-07-2011 15:31:47
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Disection de rectangle
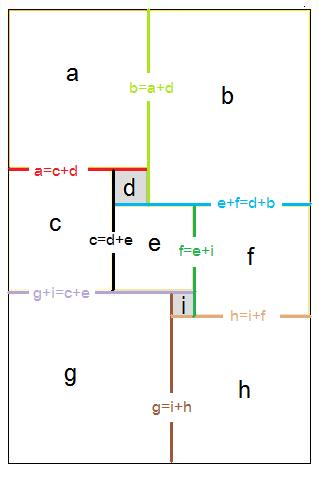
@gwen37: oui ta solution est symétrique dommage ^^. Petite astuce pour calculer plus vite:
Spoiler : [Afficher le message] Tu remarqueras que ton système peut se résoudre à la main si on le pose initialement de maniére futé ^^, par exemple dans ton cas tu peux tout exprimer en fonction de C et de E (de proche en proche) et du coup ça ne fait que 2 inconnus
#12 - 09-07-2011 17:01:00
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
#13 - 09-07-2011 20:34:15
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
dissection de rectanglz
En chipotant avec un crayon on se rend vite compte qu'il n'y a pas de solution avec peu de carrés.
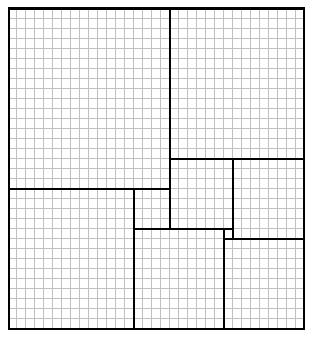
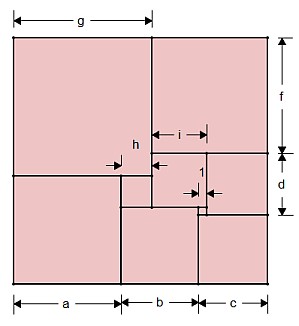
Au bout d'un moment j'arrive à un dessin qui tient la route (avec 9 rectangles qui semblent carrés). En l'absence de longueur de départ, j'attribue une longueur 1 au plus petit des carrés et j'appelle les autres a,b,c,d,f,g,h,i.
J'obtiens un paquet de petites équations que je donne à manger (séparées par des virgules) à WolframAlpha :
a+b+c=f+g
a+g=f+d+c
c=d+1
d=i+1
b=c+1
b+1=i+h
b+h=a
a+h=g
i+d=f
Bon c'est vrai qu'il y a plus d'équations que d'inconnues, mais WA n'est pas gêné et me répond : a = 14, b = 10, c = 9, d = 8, f = 15, g = 18, h = 4, i = 7
#14 - 09-07-2011 21:23:41
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Dissection de rectangl
Bravo loozer!
Tu as une des deux solutions minimales que je connaisse.
#15 - 09-07-2011 21:32:08
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
dissevtion de rectangle
Peut-on avoir un petit indice sur l'aire du rectangle ? Ou le nombre de carrés ? Ou les côtés minimaux et maximaux des carrés ?
Parce que là, je sèche, et je vois pas de méthodologie pour commencer 
#16 - 09-07-2011 22:04:21
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
dissectipn de rectangle
@L00ping007:
Spoiler : [Afficher le message] Essaye de dessiner un croquis de rectangle et remplit l'intérieur de carré (pas forcément parfait juste au pifomètre) en faisant en sorte de ne pas ajouter de carré de même taille que ceux déjà présent. Ensuite une fois l'intérieur remplis tu pourras trouver la taille des choses par calcul, et vérifier si ce croquis pifometrique correspond ou pas à une solution réelle acceptable. On se rend vite compte qu'il en faut un certain nombre mais ce nombre n'est pas si gros.
#17 - 10-07-2011 08:23:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,097E+3
#18 - 10-07-2011 09:34:35
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Dissection de rectaangle
Bravo à Gwen27!
"Même à la main, la solution symétrique aboutissait à deux carrés de même taille."
Marrant cette remarque :p comme si deux réalité mathématiques existaient entre wolfram et la main :p
PS: comme je disais plus haut il y a 2 solutions minimales.
#19 - 10-07-2011 15:39:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,097E+3
dissecrion de rectangle
Oui, bah j'en ai une, ça me suffit... Je ne suis pas trop fan des équations) Mais ce problème était bien sympa dans le genre casse-tête . Bravo. Je ne suis pas trop fan des équations) Mais ce problème était bien sympa dans le genre casse-tête . Bravo.
#20 - 10-07-2011 22:25:24
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
dissectipn de rectangle
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#21 - 11-07-2011 09:00:39
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1984
Dissection de recctangle
Il me semble que c'est ce qu'on appelle en géométrie un "rectangle parfait". C'est constructible donc (même si je n'ai plus d'exemple en tête)
#22 - 11-07-2011 09:49:58
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
dissection de recyangle
@scarta:oui c'est ca, la partie intéressante consiste à trouver comment ca se construit, ca peut se trouver avec un papier et un crayon. le cas du rectangle est abordable.
#23 - 17-07-2011 09:48:47
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Dissection de rectaangle
SOLUTION maintenant ajoutée au post de départ.
Merci à tous les participants.
#24 - 17-07-2011 10:34:40
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Dissection de recttangle
Je maintiens que pour le problème que tu nous as proposé, la proposition "prendre n'importe quel rectangle"n'était pas valable. Il y a des rectangles parfaits (qui vérifient les conditions dont on a besoin ici) et des rectangles imparfaits. On ne peut pas 'paver' un rectangle imparfait avec des carrés tous de taille différente et en nombre fini.
Si on avait décidé de partir d'un rectangle de dimensions fixées numériquement (on avait le droit a priori), on aurait pu tomber sur un cas de rectangle imparfait.
Bien que ton énoncé sous-entende qu'on aborde un cas général sans fixer de dimensions au départ pour ensuite établir un système d'équations, je pense qu'il aurait plutôt fallu aborder directement un cas particulier, en fixant les dimensions du rectangle. D'une part, ça t'aurait permis de choisir un cas non répertorié sur le net; et d'autre part, impossible de partir d'un rectangle imparfait...
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#25 - 17-07-2011 19:06:45
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
dossection de rectangle
@STHF47: Mais tu as simplement mal compris ce que j'ai écris dans l'énoncé original pourtant il y a peu de place au quiproquo.
Je n'ai jamais demandé de trouver une méthode pour étant donné un rectangle quelconque le paver de carrés j'ai laissé le choix du rectangle, voulant dire par la "prenez celui pour lequel vous pensez pouvoir le faire", ce qui n'a bien sur strictement rien à voir.
D'autre part partir d'un rectangle est une très mauvaise méthode, il fait parti du croquis comme tout le reste et intervient trivialement dans le système d’équations on détermine ses dimensions tout comme les dimensions des carrés internes si notre croquis se révèle par calcul être une solution valable.
Le système d’équations qui régit les dimensions des divers segments du croquis (y compris donc les cotés du rectangle) est très clairement linéaire à coefficients entiers. Ainsi donc tous les rapports de couples de longueurs de segments sont des rationnels et toutes solution à un facteur multiplicatif prêt est équivalente à une solution avec toutes les longueurs entières, ce que tu sembles dire et ce avec quoi j'ai toujours été parfaitement d'accord.
C'est plus clair?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum