Enigmes

Forum dédié aux énigmes et à toutes formes de jeux de logique.

Déconnexion

Tu n'es pas identifié sur Prise2tete : s'identifier.

accueil Accueil forum Forum
[+]

Pages: 1

Écrire une réponse

 #1 - 30-06-2011 21:38:35

Jackv
Elite de Prise2Tete
Enigmes résolues : 34
Messages : 3500
Lieu: 94110

Commnet faire un rectangle avec 3 lignes ? (suite)

Il existe différentes solutions pour tracer un rectangle à l'aide de 3 lignes à l'intérieur d'une feuille rectangulaire, de telle manière que ce rectangle reste symétrique par rapport au centre de la feuille.
(voir http://www.prise2tete.fr/forum/viewtopic.php?id=9137 )

En supposant que la feuille a une longueur de 29.7 cm, quelle doit être sa largeur pour obtenir un rectangle dont tous les cotés sont distants de 1 cm du bord de la feuille en employant :

- une méthode déduite de celle proposée par looozer (pas trop dur)
http://www.prise2tete.fr/upload/looozer-rectangle.jpg

- la méthode proposée par gwen (un peu plus délicat ... et je n'ai pas trouvé de j'ai maintenant la démonstration smile )
http://www.prise2tete.fr/upload/gwen27-rectangle.png

Un grand merci à tous les deux smile pour leur participation (involontaire, mais très visuelle) à cette énigme.

(Il paraitrait que pour son 500ème message, il est d'usage de proposer une énigme ? alors ... wink )

    • |
  • Répondre

#0 Pub

 #2 - 30-06-2011 21:46:12

kosmogol
Banni
Enigmes résolues : 49
Messages : 11,928E+3

Commen faire un rectangle avec 3 lignes ? (suite)

Bienvenue à un nouvel expert big_smile

http://enigmusique.blogspot.com/

 #3 - 30-06-2011 22:52:11

gwen27
Elite de Prise2Tete
Enigmes résolues : 49
Messages : 5,996E+3

comment faire un rectanhle avec 3 lignes ? (suite)

Le premier :
http://www.prise2tete.fr/upload/gwen27-pliage1.jpg

Le second :
http://www.prise2tete.fr/upload/gwen27-pliagecalcul.png

Le problème devient alors abordable 2 équations et deux inconnues ( même si je n'ai toujours pas la réponse ).

 #4 - 01-07-2011 16:03:24

Jackv
Elite de Prise2Tete
Enigmes résolues : 34
Messages : 3500
Lieu: 94110

Comment faire un rectaangle avec 3 lignes ? (suite)

Bravo à gwen big_smile pour la solution du premier problème.

En ce qui concerne le second, j'ai maintenant la solution, pas si difficile que cela, à condition de bien remarquer une particularité de la construction. wink

 #5 - 01-07-2011 16:10:23

gwen27
Elite de Prise2Tete
Enigmes résolues : 49
Messages : 5,996E+3

Comment faire un rectangle avec 3 lgines ? (suite)

Effectivement, on peut aussi se dire que la diagonale du rectangle est le double de sa largeur

l^2 + L^2 = 4l^2

Donc L= rac(3) l

Je tombe sur 18 cm de largeur à quelques centièmes près.

 #6 - 02-07-2011 09:15:07

Jackv
Elite de Prise2Tete
Enigmes résolues : 34
Messages : 3500
Lieu: 94110

Cmment faire un rectangle avec 3 lignes ? (suite)

Bravo, gwen big_smile , nous avons le même résultat pour le deuxième problème, (à partir de 2 remarques différentes mais qui conduisent à la même formule).

 #7 - 03-07-2011 22:26:50

looozer
Expert de Prise2Tete
Enigmes résolues : 49
Messages : 697
Lieu: Belgique

comment faire un revtangle avec 3 lignes ? (suite)

Bien vu smile
J'avais les dimensions mais pas la méthode de pliage, pas très utile roll

 #8 - 04-07-2011 09:24:48

Jackv
Elite de Prise2Tete
Enigmes résolues : 34
Messages : 3500
Lieu: 94110

Comment faire un rectangle ave c3 lignes ? (suite)

Bravo encore à gwen big_smile ; dommage qu'il ait été le seul à apporter une réponse à cette énigme... neutral

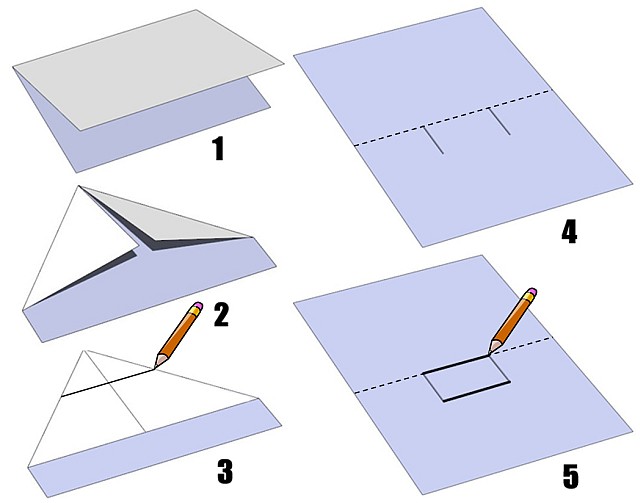
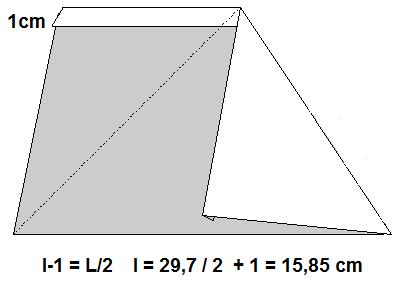
Pour le 1er pliage,  l = L/2 + 2 = 15.85 cm.

En ce qui concerne le 2ème pliage, l'idée de base est de considérer les dimensions du rectangle plutôt que celles de la feuille.
Soient L1 = L - 2 = 27.7 cm sa longueur et l1 = l - 2 sa largeur.

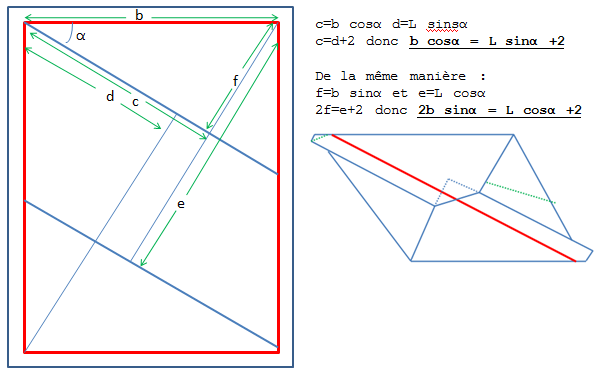
La 2ème chose à voir, c'est que le parallélogramme formé par ce rectangle plié est aussi un losange puisque ses diagonales sont perpendiculaires.

L'étape suivante est de s'apercevoir que, sur la figure de gwen dans son message 3, l'angle [latex]a[/latex], compte tenu de la symétrie due au pliage, vaut 30°.
Dans ce triangle rectangle, le petit coté de l'angle droit est donc égal à la moitié de l’hypoténuse et la somme de ces 2 cotés est égale à L1.

Pythagore nous donne :
[TeX]l1 = \sqrt (4/9 - 1/9) *L1[/latex]     donc     [latex]l = \sqrt (3)/3 * L1 + 2[/TeX]
                                 l =  17.99 cm

 

Écrire une réponse

Pages: 1

Réponse rapide

Rédige ton message
| | | | Upload | Aide
:) :| :( :D :o ;) :/ :P :lol: :mad: :rolleyes: :cool:
Sécurité

Répondez (numériquement) à la petite énigme suivante : 

Si il y a 88 pommes et que vous en prenez 44, combien vous en avez ?

Mots clés des moteurs de recherche

Mot clé (occurences)
Dessiner un rectangle avec 3 traits (26) — Comment faire un rectangle avec 3 traits (22) — Rectangle avec 3 traits (18) — Enigme a faire sur papier (15) — Comment faire un rectangle (13) — Faire un rectangle avec 3 traits (13) — Dessiner un rectangle avec 3 lignes (11) — Les lignes dans le rectangle (9) — Dessiner un rectangle avec trois traits (9) — Rectangle avec 3 lignes (9) — Comment tracer un rectangle au sol (9) — Un rectangle avec 3 traits (8) — Rectangle avec trois traits (8) — Rectangle a 3 traits (8) — Dessine un rectangle avec trois traits (7) — Comment faire un carre avec 3 traits (7) — Rectangle 3 traits (6) — On considere une feuille de papier de dimensions 21 cm et 29.7 cm (6) — Comment faire un rectangle avec 3 lignes (6) — Comment tracer un rectangle (6) — Comment faire les trois traits (6) — Dessiner un rectangle avec trois lignes (5) — Comment dessiner un rectangle avec 3 traits (5) — Comment faire un rectangle avec trois lignes (5) — Rectangle 3 lignes (5) — Faire un rectangle avec trois traits (4) — Rectangle a 3 lignes (4) — Enigme visuelle avec reponse (4) — Dessiner un carre avec 3 traits (4) — Rectangle a trois trait (4) — Comment faire les 3 traits (4) — Rectangle avec 3 ligne (4) — Comment faire un rectangle avec trois traits (4) — Devinette a faire sur papier (4) — Enigme a faire sur feuille (4) — Tracer un rectangle avec 3 traits (3) — Comment dessiner un rectangle avec trois traits (3) — Rectangle en 3 lignes (3) — Faire un losange avec une feuille (3) — Probleme pythagore pliage feuille 21 cm large (3) — Faire un rectangle avec 3 trait (3) — Dessiner un rectangle en 3 traits (3) — Dessiner rectangle avec 3 traits (3) — E rectangulaire a fabriquer (3) — Carre a 3 traits (3) — Devinette sur feuille (3) — Un rectangle avec 3 lignes (3) — Les enigmes avec solution (3) — Faire un rectangle avec 3 lignes (3) — Comment dessiner un rectangle avec 3 lignes (3) — Solution dessiner un rectangle avec trois traits (3) — Comment fair rectangle 1*2 (3) — Faire un carre en trois trait (2) — Dessiner 2 rectangles different avec 22 (2) — Construction par pliage d un parallelogramme (2) — Triangle.avec 3 trait (2) — Faire un rectangle avec trois lignes (2) — Comment dessiner un rectangle au centre d une feuille (2) — Rectangle au 3 (2) — Comment fait le carre de 3 (2) — Rectangle avec trois ligne (2) — La feuille avec rectangle (2) — Faire un carre en trois traits (2) — Comment faire le symetrique d un cercle (2) — Main tenant une feuille (2) — Comment faire un carre (2) — Longueurs possibles des cotes du rectangle symetrique (2) — Comment faire une enigme (2) — Faire un carre en 3 ligne sur une feuille (2) — Rectangle a 3lignes (2) — Trace un rectangle avec 3 traits (2) — Comment former un carre avec 3 allumettes (2) — Comment dessiner un rectangle en trois lignes (2) — Pour faire un rectangle sur le sol (2) — Construire un rectangle avec 3 traits (2) — Comment faire rectangle avec 3 traits (2) — Comment fabriquer 1 carre avec 3 triangles et un losange (2) — Comment dessiner un carre avec trois trait (2) — Faire un message enigme (2) — Carre trois trait (2) — Faire un carre avec 3 traits (2) — Comment faire un rectangle au milieu d une feuille (2) — Dessiner un carre avec trois barres (2) — Problemes equations a 2 inconnues. (2) — Dedans le rectangle contenant 4 triangles1 carre et 1 losange (2) — Faire un carre avec 3 feuilles (2) — Carre 3 lignes (2) — Feuille a4 faire des losanges 3 cm (2) — Comment faire des enigmes (2) — Fair un carre avec 3 trait (2) — Enigme du rectangle en 3 traits (2) — Carre avec 3 traits (2) — Longueur et largeur d un rectangle (2) — Rectangle avec trois lignes (2) — Comment faire un carre avec des rectangles (2) — Faire un carre en 3 ligne (2) — Comment faire un rectangle en papiere 10 cm (2) — Avec 7 lignes tracer un losange un rectangle et un carre (2) — Dessiner un rectagle avec 3 lignes (2) — Comment on fait un rectangle avec 3 lignes (2) — Enigme solution carre avec trois lignes (2) — Comment tracer un carre au sol (2) — Rectangle a 4 lignes (2) — Comment construire un rectangle (2) — Comment construire un rectangle en 3 (2) — Reponse un rectangle avec 3 traits (2) — Dissection losange en triangle equilateral (2) — Comment faire un rectangle avec trois lignes droites (2) — Comment faire un triangle avec 3 traits (2) — Enigme rectangle (2) — Tracer un rectangle avec 3 lignes (2) — Rectangle a trois ligne (2) — Fabriquer un carre en papier (2) — On considere une feuille de papier de dimension 21 cm et 29.7 cm (2) — Enigme a faire sur papier dessin (2) — Demonstration de faire un carre avec la feuille (2) — Comment tracer un rectangle au centre d une feuille (2) — Ecrire en rectangle en 3 lignes (2) — Dessinez un rectangle avec trois traits (2) — Comment faire un carre enigme (2) — Comment tracer une suite (2) — Quelle sont les differents rectangle (2) — Comment faire les trois traits sur (2) — Comment tracer un rectangle de 18 cm (2) — Pliage faire 1/3 dans un rectangle (2) — Comment dessiner un rectangle avec trois lignes (2) — Comment faire un carre en papier (2) — Former un carre avec un rectangle (2) — Enigme un carre avec 3 l a l interieur (2) — Rectangle trois lignes (2) — +rectangle en 3 trai (2) — Enigme 8 triangles dans un rectangle a partir de 3 lignes (1) — Rectangle en 3 tres (1) — Solution un trait rectangle (1) — Comment desinerun triangle rectangle a engle droit (1) — Dessinee un tectangle avec trois traits (1) — Dessiner un triangle aves 3 traits (1) — Comment rectangle avec 3 lignes solution (1) — Comment faire un carre a 4 ligne (1) — Solution comment faire un rectangle en 3 trait (1) — Comment faire 3 lignes (1) — Comment dessiner un rectangle avec 3 trait (1) — Recatngle avec 3 traits (1) — Comment faire un carre centre dans une feuille (1) — Dessiner 8 carre avec 12 lignes (1) — Comment construire des diferent rectangle (1) — Comment faire un carre avec des formes (1) — Enigme a faire (1) — Tracer un rectangle a partir de ses diagonales (1) — Comme faire des traits sur un (1) — Triangle 3 traits probleme (1) — 8 avec 3 traits (1) — Tracer un carre au centre de la feuille (1) — 3 carres devenant rectangle (1) — Dessiner un carre avec trois traits (1) — Comment faire un rectangle en papier (1) — Enigme carre avec 3 cotes (1) — Solution dessiner un rectangle avec 3 lignes (1) — Enigme rectangle avec 3 trait (1) — Test carre avec 3 lignes (1) — Differente solutions du trait carre (1) — Comment faire un carre a partir de deux (1) — Tracage du trait carre avec la formule 3 4 5 (1) — Comment situer de trait symetrique dans un carre de 12 cm (1) — Comment faire le s avec les 3 traits (1) — Dessinez un rctangke avec trois traits (1) — Faire un carre avec trois trait (1) — Dessinez+un+rectangle+avec+trois+traits (1) — Comment faire un rectangle a 3 (1) — Dessiner rectangle avec 3 lignes solution (1) — Solution du probleme des 3 triangle moins 2 trait (1) — Faire un losange avec deux traits (1) — Comment tracer la symetrie d un rectangle avec un trait (1) — Comment faire les lignes sur la feuille de papier (1) — Comment faire un carre avec 5 trait (1) — Dessinez rectangle avec 3 traits (1) — Dessiner un rectangle abec 3traits (1) — Reponse dessiner un rectangle avec trois lignes (1) — Comment tracer un rectangle sur une feuille (1) — Un carre avec 3 barres (1) — Dessiner rectangle en ligne (1) — Comment obtenir avec trois carre obtenir un rectangle (1) — Enugme a faire avec une feuille (1) — On considere une feuille de papier de dimensions 21 cm et 29.7cm.on plie cett (1) — Fabriquer un carre par pliage (1) — Probleme math : aire d un rectangle inscrit dans un triangle (1) — Comment faire trois traits (1) — Comment faire un rectangle avec 3 trait (1) — Comment faire un carre avec des trinagles (1) — Carre avec trois trait (1) — Faire un carre en 3 trait (1) — Comment faire un carre avec 2 lignes dans le milieu (1) — Avec deux traits dessiner un triangle (1) — Comment faire un rectangle en java (1) — La devinette des traits (1) — Enigmes visuelles avec solution (1) — Formuler enigme en ligne (1) — Comment creer des enigmes (1) — Enigme ligne dans un rectangle (1) — Un retangle et 4 lignes (1) — Carre a trois trait (1) — Creer des enigmes .3 (1) — Faire un carre avec un trait (1) — On considere une feuille de papier de dimension 21 cm et 29.7 on plie cette feuille (1) — Enigme feuille pliage (1) — Comment faire un rectangle avec deux donne (1) — Dessiner carre 3 trait solution (1) — Un rectangle a trois ligne (1) — Comment faire 1 carre avec plusieur triangle rectangle different (1) — Dessiner un rectangle avec 3 traits solution (1) — Enigme un rectangle avec 3 lignes (1) — Test dessiner un carre avec 3 ligne (1) — Comment faire un carre avec 3 allumettes (1) — Comment commencer un rectangle sur (1) — Enigme carre par 3 lignes (1) — Un rectnagle avec trois traits (1) — Comment faire un rectangle avec trois ligne (1) — Tracer un rectangle en 3 lignes (1) — Comment faire un rectangle en 3 d en mn en cm (1) — Enigme dessine un rectangle avec 3 traits (1) — 2 rectangle 2triangles 4points 10traits (1) — Enigme rectangle trais (1) — Comment faire un rectangle en trois lignes (1) — Enigme dessiner rectangle 3 lignes (1) — 4 manieres de trouver le meme resultat dans un rectangle (1) — Avion papier dessin (1) — Dessiner un triangle avec deux traits (1) — Comment fabrique une avion avec les feulle (1) — Losange avec 3 trait (1) — 1 rectangle avec 3 traits (1) — Construire un carre avec trois (1) — 1 rectangle avec 1 carre et3 rectangles a l interieur aire construction geogebra (1) — Dessiner un rectangle en trois traits (1) — Redctagle avec double ligne (1) — Dessiner un carre avec ses (1) — Un carre avec 3 traits (1) — Rectangle avec trois trait (1) — Comment construire ?3 (1) — Suite logique et rectangle avec 3 trait (1) — Enigme dessiner.un rectangle avec3 lignes solution (1) — Carre 3traits (1) — Dessinez un rectangle avec trois lignes (1) — Un triangle rectangle avec trois trai (1) — Comment construire un triangle rectangle avec 3 allumettes (1) — Comment faire un carre avec un triangle (1) — Faire le tour du carre avec 3 ligne (1) — Trace un carre au sol (1) — Fabriquer un carre avec trois traits (1) — Losanges... (1) — Faire un carre zvec trois trzit (1) — Tracer un triangle rectangle avec 3 allumettes (1) — Comment trouver la longueur d un cote qui est a l interieur d un rectagle (1) — Enigme visuelle avec solution (1) — Comment tracer un rectangle en utilisant le bord de la feuille (1) — Comment faire un losange avec 4 carre a linterrieur sans repasser sur les trait (1) — Comment faire carre avec trois ligne (1) — Comment faire un carre avec trois a (1) — Enigme avec rectangle (1) — Comment faire un regtangle (1) — Enigme mathematique dessiner un triangle avec trois ligne (1) — Faire 2 rectangles et 3 triangles avec une forme (1) — Comment en trois lignes (1) — Rectangle avec 3 trait (1) — Test logique : dessiner un rectangle en 3 lignes (1) — Rectangle en trois des (1) — Un triangle en 3 lignes (1) — Solution de devinette en ligne (1) — Enigme comment tracer un rectangle en trois trats (1) — Devinette tracer un rectangle avec 3 traits (1) — Enigme avec losange (1) — Rectangle avec 3 barres (1) — Comment faire un carre avec 3 triangle rectangle (1) — Test rectangle avec trois trait solution (1) — Test dessiner un carre avec 3 trai (1) — Faire un rectangle avec un carre (1) — Comment construire triangle rectangle aire =18cm (1) — Avec une ficelle de 18cm comment construire un rectangle d une aire la plus grande (1) — Comment dessiner un carre (1) — Faire un triangle avec un rectangle (1) — Creer un rectangle au sol (1) — Dessinee rectangle trois lignes (1) — Desiner un carre avec 3 lignes (1) — Dessiner un resctangle avec 3 ligne (1) — Enigme dessin (1) — Triangle rectangle avec traits de construction (1) — Trace un rectangle avec 3 trait (1) — Comment fabriquer 46 avec 3 -2-6-3-6 (1) — Comment tracer un carre de 3 cm de cote dans un rectangle (1) — Carre avec trois traits (1) — Rectangle en 3 traits (1) — Rectangle en trois ligne (1) — Comment fabrique des avion de papier (1) — Differente facon de plier une feuille pour ecrire son nom (1) — Dessiner un rectangle sur 3 lignes (1) — Rectangle a trois trai (1) — Comment tracer un rectangle avec 3traits (1) — Enigme carres et lignes (1) — Tracer un rectangle avec 3 donnee (1) — (1) — Faire un triangle a partir de trois traits (1) — Faire un rectangle de 18cm avec 8 triangle (1) — Rectangle trois traits (1) — Comment trace en 9 traits un losange un rectangle et un carre (1) — Faire un carre avec trois lignes (1) — Comment faire un losange avec du papier (1) — Faire un carre avec trois allumettes (1) — Enigme rectangle 3 trait (1) — Test de logique faire 2 carres avec 3 cotes (1) — Tracer un rectangle avec trois traits (1) — Faire+un+rectangle+avec+trois+traits (1) — Egimes faire un tracer dans 12 carres (1) — Comment faire 1 rectangle (1) — Devinette carrer 3 ligne (1) — Comment bien faire un rectangle (1) — Dessiner un triangle avec trois lignes (1) — Devinette comment faire un carre avec (1) — Rectangle avec 3 trait enigme (1) — Formule trai carre (1) — Enigme comment faire un carre avec trois traits (1) — Comment faire un trait carre (1) — Rectangle en 3 trait (1) — Dessiner un carre avec trois traiy (1) — Feuille avec carres et des rectangles (1) — Comment dessiner un rectangle huit carre (1) — Enigme difficile construire un rectangle avec une figure (1) — Faire un carre avec trois traits (1) — Comment faire une tour rectangle avec une feuille a4 (1) — Solution trace un carre (1) — Comment tracer un rectangle avec 3 traits (1) — Tracer un carre au sol (1) — On considere une feuille de papier de dimensions 21 cm et 29.7cm. (1) — Tracer un suite (1) — Enigme deux carre en 3 traits (1) — Methode du trait carre (1) — Rectangle a 3 trait (1) — Comment fair des devinette (1) — Comment tracer un rectangle connaissant une diagonale (1) — Comment faire des s avec des feuilles rectangulaires (1) — Comment tracer un triangle avec un feuille (1) — Un carre avec 3 trait (1) — Logique dessine une carre avec 3ligne (1) — Math faire un triangle rectangle avec 3 carre (1) — Enigme ligne carre (1) — Trace au sol rectangle (1) — Comment faire un carre en 3 traits (1) — Enigme rectangle trait (1) — Plier un rectange en losange (1) — Dessiner un rectangle et trois traits (1) — Dessiner rectangle avec trois traits (1) — Dessiner un triangle avec 2 barres (1) — Tracer un rectangle avec un trait enigme (1) — Solution d un carre avec 3 lignes (1) — Comment faire 1 carre avec 3 trai (1) — Faire un losange avec 3 traits (1) — Dessiner un carre avec 3 traits la solution (1) — Enigmes comment tracer un rectangle (1) — Enigme dessiner un rectangle avec trois traits (1) — Triangle avec deux traits enigme (1) — Enigme dessiner un carre barre (1) — Comment dessiner un rectangle (1) — Methode pour tracer un rectangle (1) — Comment faire un losange avec trois traits (1) — Solution carre a 3 trait (1) — Faire u n restangle avec 3 traits (1) — Comment faire un carre en papier (1) — Pour faire 3 lignes (1) — Faire trois rectangles en un (1) — Dessine un rectangle avec 3ligne (1) — Rectongle avec trois traits (1) — Methode la plus simple pour tracer un rectangle au sol (1) — Reponse rectangle en trois traits (1) — Comment faire pour que 3 rectangles aient le meme perimetre dans un rectangle (1) — Dessinez un rectangle avec 3 traits (1) — Comment faire un rectangle avec 3traits (1) — Tracer un rectangle avec 3 trait (1) — Fais un carre avec 3 trai (1) — Carre 3 lignes enigme (1) — Logique comment faire un carree avec trois traits (1) — Comment faire un carre avec une feuille rectangulaire (1) — Devinette pliage feuille (1) — Formee un losange avec un triangle rectangle (1) — Tracer rectangle carre losange cm2 (1) — Comment fair rectangle avec 3 carre (1) — Comment faire un carre avec trois traits (1) — Solution avec 3 droites (1) — Rectangle trois traits donne 14 rectangle (1) — J ai un rectagle de longueur 12 cm et de largeur 4 cm methode pour trouver tous les rectangles qui passent par la diagonale (1) — Faire un rectangle (1) — Dessiner un rectangle avec 3 traits en c (1) — Comment faire 3ligne (1) — Trace trois rectangles differents 18cm (1) — Comment obtenir un carre avec 49 (1) — Coment faire un carre avec 3 (1) — Faire un carre avec 3 trais (1) — Comment faire trois lignes (1) — Former un carre avec 3 ligne (1) — Rectangle3 d comment faire (1) — Dessins devinettes avec feuille de papier (1) — On considere une feuille de dimensions 21 cm et 29.7 cm. on pile cette feuille (1) — Enigme comment faire un losange avec trois lignes (1) — Construire un carre avec trois trait (1) — Creer des enigme par pliage (1) — Comment faire un losange avec 3 trait (1) — Comment tracer un carre avec trois traits (1) — Faire 1 carre en 3 traits (1) — Devinette dessin avec rectangle triangle trait (1) — Comment un rectangle rectangle un un 3 3 (1) — Rectangle avec trois traits solution (1) — Comment faire un rectangle en trois d (1) — Comment faire un carre avec trois triangle et un carre (1) — Rectangle avec 3lignes (1) — Enigme a dessiner (1) — Dessiner un rectangle avec une aire de 20 cm2 et 1 perometre de 18 cm (1) — Comment dessiner un carre sur le sol (1) — 1 carre avec 3 lignes (1) — Un rectangle avec trois traits (1) — Devinette comment faire un 7 en employant trois 6 (1) — Enigme rectangles 3 lignes (1) — Rectangle 3 droites (1) — Tracer des rectangle jeu en ligne (1) — Losanges carres rectangles (1) — Dessine un rectangle avec 3 traits (1) — Un rectangle avec trois lignes (1) — Trois traits pour faire carre (1) — Pliage pour faire un rectangle (1) — Comment dessiner un losange avec des carres dedans (1) — Un rectangle a trois tres (1) — Comment dessiner un carre a troi traiy (1) — Methode tracer un carre (1) — Comment obtenir un rectangle (1) — Triangle avec 3 lignes (1) — Faire un trace avec trois traits (1) — Retangle 3 traits (1) — Comment tracer un rectangle? (1) — Un carre avec trois traits (1) — Enigme mathematique un rectangle en trop (1) — Aire 10cm2 (1) — Carr? 3 (1) — Jeux reflexion carre en 3 traits (1) — Comment tracer au sol un rectangle pour construction (1) — Logique avec 1 trait (1) — Comment faire un rectangle avec 3 ligne (1) — Faire un triangle avec 3 trai (1) — Tracer rectangle et carre ausol (1) — Comment tracer un carre (1) — Comment faire un carre avec 5 tr ait (1) — Enigme des 3 rectangles en faire qu (1) — Feuille avec 21 rectangle (1) — Enigme expert avec reponse (1) — Faire losange sur feuille a 4 (1) — Differentes facons de faire un avion en papier (1) — Enigme dessiner un rectangle avec 3 trait (1) — Faire un rectangle au sol (1) — Comment plier un rectangle pour avoir un losange (1) — Enigme carre avec 3 traits (1) — Comment faire un rectangle avec 3 allumettes (1) — Enigme faire un cochon avec 3 lignes (1) — Un rectangle avec ses formules (1) — Comment tracer un rectnagle avec 3 dimensions (1) — Enigme rectangle avec 3 trais (1) — Faire un carre trois traits droits ? (1) — Enigme avec des traits trop dure (1) — Carr? ? 3 traits (1) — Tracer un carre et un rectangle avec 5 droites (1) — Dessin un retangle (1) — Faire une enigme (1) —

Pied de page des forums

P2T basé sur PunBB
Screenshots par Robothumb

© Copyright 2002–2005 Rickard Andersson
Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact
© Prise2tete - Site d'énigmes et de réflexion.
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.
Flux RSS de Prise2Tete Forum Jeux & Prise2Tete Test & Prise2Tete Partenariat et Publicité sur Prise2Tete