 |
#1 - 25-08-2022 10:57:58
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
Décimales de ip
Saurais tu donner
donner les cents premiers billions des décimales de pi avec une erreur de moins de 1/100 000
?
Lélio Lacaille - Du fagot des Nombreux
#2 - 25-08-2022 11:45:57
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
décumales de pi
Ben non. c'est au dessus du record actuel
(Je viens de vérifier, en effet c'est 62,8 billions)
#3 - 25-08-2022 17:52:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
écimales de pi
Je vais être gentil , je vais te donner les cent premiers quadrilliards de décimales de [latex]\pi[/latex] avec une erreur de moins de 1 , après tu en feras ce que tu voudras : [latex]\pi\approx 3,0000\cdots[/latex]
Vasimolo
#4 - 25-08-2022 21:02:15
- ptitours63
- Habitué de Prise2Tete
- Enigmes résolues : 49
- Messages : 32
Décimales d pi
Pas sûr d’avoir bien compris la question…mais je tente 3,14159 suivi de n’importe quels chiffres jusqu’à faire cent billions de décimales (par exemple que des 0) ??
En utilisant les 5 premières décimales de Pi, je devrais avoir un écart inférieur à 1/100’000.
#5 - 26-08-2022 10:32:00
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
Décimales de p
Il paraitrait que c'est possible en fait. Alors je précise pourquoi je ne suis pas d'accord : si la question est en fait "donner les cents premiers billions des décimales de <pi avec une erreur de moins de 1/100 000>" et pas "donner les <cents premiers billions des décimales de pi> avec une erreur de moins de 1/100 000", alors il y a une réponse bien entendu, c'est 3.14160000....000 par exemple, mais ça ne rentre pas (à mon sens) dans la catégorie "énigme mathématiques"
#6 - 27-08-2022 01:47:58
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
Décimales ed pi
Je précise qu'il s'agit ne s'agit pas d'une erreur sur pi (la solution serait triviale et donnée par certains avec le jugement qu'elle mérite (sourire)², et le défi serait inexistant), mais bien concernant les décimales données.
Lélio Lacaille - Du fagot des Nombreux
#7 - 27-08-2022 18:54:51
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
décimalrs de pi
Certains ont évoqué qu'il était possible de comprendre l'énoncé d'une façon triviale (concernant pi et non pas ses décimales), tout en reconnaissant que tel quel, il s'agit bien des décimales.
Mais effectivement l'exigence n'était peut-être (sourire) pas celle qu'ont ajouté ceux qui se sont frottés à la question.
Nul part on ne demande un ordre précis.
Ceci clarifié, tout devient plus simple :
Il y a deux réponses possibles.
Elles s'appuient sur le fait
(merci de démontrer le contraire, je suis toujours heureux de congédier une erreur)*
que les décimales de pi peuvent s'apparenter du point de vue de leurs collections de chiffres, à un tirage aléatoire.
Ainsi
on peut proposer
1) Dans le cas où toutes les décimales connues sont accessibles :
toutes ces décimales, suivies d'un tirage aléatoire des autres décimales
dans ce cas la mystification ne sera pas détectable.
2) Plus simplement pour ces décimales demandées
on peut se contenter de proposer
"il y a parmi ces 100 billions de décimales
10 billions de 0
10 billions de 1
10 billions de 2
10 billions de 3
...
10 billions de 9"
Le nombre important de décimales demandées assurant une répartition proche de cette proposition de réponse
avec un écart très inférieur à 1/100 000ème
(Je suis certain que quelqu'un ici saura donner l'écart entre le nombre respectif de décimales pour un tirage de 100 billions de chiffres. (sourire)²
ou une borne pour parvenir sous cet écart))
Merci à ceux qui ont participé.
___
*bis
Lélio Lacaille - Du fagot des Nombreux
#8 - 29-08-2022 07:52:44
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
Décimales de pii
Elles s'appuient sur le fait
(merci de démontrer le contraire, je suis toujours heureux de congédier une erreur)*
que les décimales de pi peuvent s'apparenter du point de vue de leurs collections de chiffres, à un tirage aléatoire.
Alors d’une on ne peut pas prouver le contraire d’un fait. C’est un fait.
De deux, on ne peut pas non plus énoncer un constat comme étant un résultat prouvé. C’est donc plutôt à toi de prouver ton résultat.
De trois, aléatoire ne signifie pas équiprobable. Et là encore rien ne le prouve. Je renvoie les sceptiques à se documenter sur la loi de Benford par exemple : c’est certes un constat empirique mais enfin ça montre bien que parfois l’intuition concernant l’aléatoire est fausse.
Pour ne pas rester dans l’abstrait : tu poses en constat que Pi serait un « nombre normal en base 10 » - phrase qui correspond peu ou prou à ton affirmation, en l’espèce que tout chiffre est équiprobable.
Je te renvoie donc à la page Wikipedia de Pi. Il y est justement mentionné « Par ailleurs, le développement décimal de π ouvre le champ à d'autres questions, notamment celle de savoir si π est un nombre normal, c’est-à-dire que ses successions finies de chiffres en écriture décimale sont équiréparties. A fortiori, π serait alors un nombre univers, ce qui signifie qu'on pourrait trouver dans son développement décimal n'importe quelle suite finie de chiffres. En 2006, il n'existait pas de réponse à ces questions »
Je te confirme qu’en 2022 non plus.
Alors ok, pour être 100% formel et factuel, je sais que je n’ai pas prouvé que ton résultat est faux 
Mais enfin si tu as une démonstration de la normalité de Pi, je connais une ou deux revues dans lesquelles tu pourrais publier un article qui fera date !
Edit : merci ceci dit. Grâce à cette page Wikipedia je viens de retrouver le nom de Jean-Luc Delahaye, que je n’arrivais pas à retrouver depuis deux mois ! 
#9 - 29-08-2022 15:02:40
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
décimaleq de pi
Grand merci à Scarta
Cette précision que tu donnes corrige très justement ma réponse
Ce n'est pas un fait, c'est une hypothèse .
[Je te remercie pour la proposition de publication.
Je me contente modestement d'avoir quelques suites dans l'OEIS, cela c'est encore à ma portée (sourire)²]
Il y a deux choses dans ma question
-1- le jeu qui est fait sur le pari perceptif (certains ont dû ajouter la notion d' "ordre" qui n'est pas dans la question)
-2- et cette hypothèse qui attend son Andrew Wiles,
Ma proposition n'avait que la prétention de faire sourire
en rapport avec la raison 1
(suis curieux de savoir si, ne serait-ce que quelques secondes, tu t'y es laissé prendre)
et la réponse est ... "probablement" valide (sourire)² si on considère que quelques billions de décimales l'ont testée.
(Mais tu as parfaitement raison de dire que le doute 2 meurt)
Cordialement
PS : Tu devrais ne faire qu'une bouchée de l'énigme "L'horloge qui fait plaisir"
Lélio Lacaille - Du fagot des Nombreux
#10 - 30-08-2022 01:09:04
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
Décimales de ip
En réfléchissant encore à propos de la réponse de Scarta
j'ai pensé à la fourmi de Langton et à ce qui finit par "émerger" de son "comportement"
On peut effectivement imaginer que de cette régularité dans l'équipartition des chiffres de 0 à 9 dans l'écriture de pi en base 10, puisse émerger ici aussi une singularité non apparente dans les 64 billions premières décimales.
Je penche pour l'inexistence d'une telle singularité, pour une raison qui s'éloigne un peu de la rigueur mathématique (quoique), à savoir le sens même du nombre pi, rapport de deux grandeurs qui n'ont rien du monde "numérique", lieu de la discontinuité par excellence, et qui ont tout du monde analogique, qui lui n'est pas en rupture.
Là aussi, cela m'enrichirait que l'on conteste cet argument.
...
Lélio Lacaille - Du fagot des Nombreux
#11 - 30-08-2022 10:32:14
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
Décimmales de pi
Avec plaisir sauf que j’ai rien compris 
Quoique… le rapport 2.pi / pi fait bien intervenir des grandeurs que tu qualifies d’analogiques (j’aurais dit non algébrique personnellement) et pourtant c’est une constante entière.
#12 - 30-08-2022 11:11:38
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
Décimales d pi
(Où se situe ce rien ?)
L'analogie dont je parle
réside dans la définition de pi
l'essai de traduction de ce "rapport" qu'il y a entre le cercle et le carré
par un nombre que l'on ne parvient pas à cerner par un calcul aussi compliqué qu'il soit
ne me semble pas pouvoir faire émerger une singularité (indice en est les billions de décimales "mornes")
Nous sommes là dans ce qui précède la conjecture, laquelle précède la preuve
à savoir l'intuition (sourire)²
___
Pas plus que la théorie de l'émergence de la conscience, à partir d'automatismes très compliqués, ne me semble plausible. (passage du compliqué au complexe)
(En espérant ne pas avoir exabusé par des propos borderline /mathématiques)
Lélio Lacaille - Du fagot des Nombreux
#13 - 30-08-2022 12:20:13
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
Décimaales de pi
scarta a écrit:Avec plaisir sauf que j’ai rien compris 
Quoique… le rapport 2.pi / pi fait bien intervenir des grandeurs que tu qualifies d’analogiques* (j’aurais dit non algébrique personnellement) et pourtant c’est une constante entière.
Tout à fait et c'est bien naturel
Deux grandeurs parfaitement analogues vont précisément avoir un rapport réduit à une constante entière
Pi* révèle les différences de "nature" (de haut niveau)
du carré et du cercle qui lui est relatif
En fait le nombre qui traduit ce rapport est pi/4
(Le rapport entre l'aire d'un cercle et le volume qu'il engendre par sa révolution dit tout de "leur rapport" (sourire)²
Le rapport entre le périmètre du plus grand triangle équilatéral inscrit dans un carré et le périmètre de celui-ci n'est pas transcendant (sourire)²²)
C'est tout le principe des rapports
faire disparaitre des dimensions du même ordre.
Et mettre en évidence celles qui ne le sont pas.
Le rapport est précisément l'outil de base de l'analogie
On dit parfois "cela n'a aucun rapport"
C'est un raccourcis de "le rapport de ces deux ... n'est pas simplifiable"
(ils n'ont rien en commun qui permet de simplifier leur rapport)
___
J'utilise analogique et numérique en rapport avec complexe et compliqué
c'est plus général
et permet de faire le joint au-delà du cadre des mathématiques.
Un airbus est compliqué
un cheveux est complexe
Lélio Lacaille - Du fagot des Nombreux
#14 - 30-08-2022 20:45:57
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
décimales de oi
ok j'ai compris ce que j'avais pas compris : en fait, je fais des maths 
Attention, je n'ai rien contre la poésie hein. C'est juste que c'est pas mon truc, au même titre que la calligraphie ou le saut à la perche.
Mais... si je puis me permettre, tu auras tout autant de mal à cerner toutes les décimales de "racine de deux" que celles de Pi, et c'est pourtant la diagonale d'un bête carré de côté 1.
#15 - 30-08-2022 21:22:06
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
décimales de po
Et pour revenir à la question initiale : je n'ai malheureusement pas l'espace disque nécessaire pour calculer le résultat sur 10^11 décimales 
Je l'ai fait pour un milliard ceci-dit. Et ce que je vois me pousse à te donner raison statistiquement parlant pour 100 milliards avec moins de 1/100000 erreurs (soit moins d'un million d'erreurs).
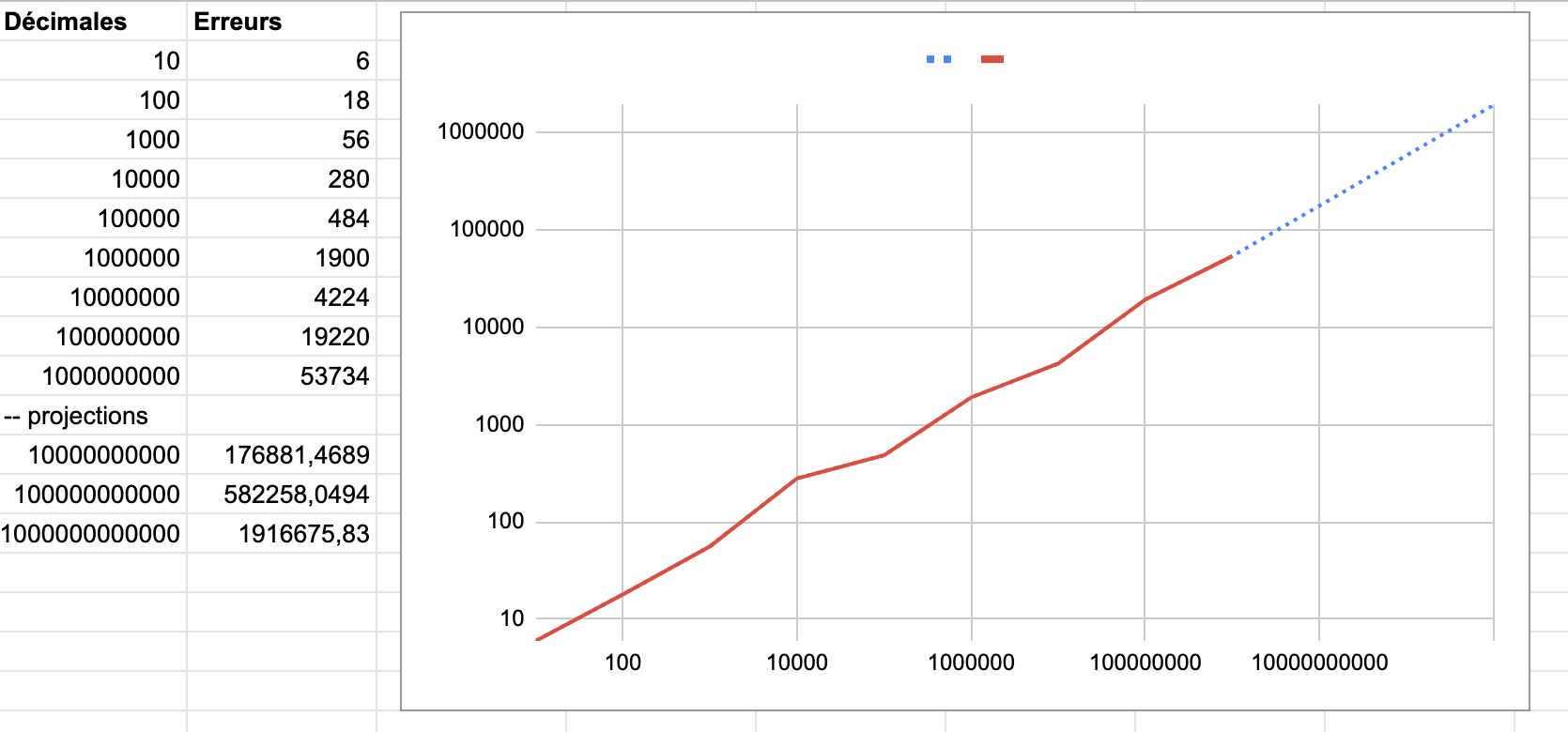
En pointillé la projection (sous reserve que le comportement soit le même), on n'atteindra le million d'erreur qu'entre 100 et 1000 milliards
#16 - 31-08-2022 04:53:35
- aunryz
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 932
- Lieu: Nicastro / Tronville
décimames de pi
scarta a écrit:ok j'ai compris ce que j'avais pas compris : en fait, je fais des maths 
Attention, je n'ai rien contre la poésie hein. C'est juste que c'est pas mon truc, au même titre que la calligraphie ou le saut à la perche.
Mais... si je puis me permettre, tu auras tout autant de mal à cerner toutes les décimales de "racine de deux" que celles de Pi, et c'est pourtant la diagonale d'un bête carré de côté 1.
Oui, je suis content que tu sois venu sur ce terrain là
qui permet pour revenir à la notion de rapport
de cerner la différence qu'il y a entre
- D'une part le rapport du côté du carré sur sa diagonale (ou l'inverse ... qui donne un quotient ayant la même signification ... un rapport du même "calibre")
(Ou encore du périmètre du carré et du plus grand triangle inscrit)
- Et d'autre part le rapport de l'aire du carré et de celui du cercle circonscrit.
Dans l'un des cas on obtient un nombre d'une autre qualité, pas une bête racine carrée, mais un nombre transcendant (sourire)²
Tu nommes poésie l'utilisation que je fais de ce que l'on trouve dans les mathématiques à un autre niveau - comme le sens profond du mot rapport (je fus prof de maths) ce que dans le PEI (Programme d'Enrichissement Instrumental : méthode de remédiation cognitive) on nomme transposition ou principe de généralisation.
En France on fait des maths pour les maths, sans vraiment transposer et donner du sens aux concepts.
C'est pour cela d'ailleurs que les fondamentaux (le point, la droite, etc.) ne sont plus en enseignés, mais utilisés
On mettait trop en danger l'élève (sourire)² avec des notions comme le zéro du point et l'infini de la droite.
(Ce qui donne au niveau compréhension des nombres et des étendues, des trucs comme :
"le dépassement d'un mobile qui va plus vite qu'un autre, dure un certain temps pendant lequel les deux mobiles sont sur une même ligne"
avec impossibilité d'en décoller
" si si c'est un temps très court mais il existe !" ... jusqu'à disjoncter.
Donc pour en revenir aux rapports
Le rapport de la circonférence de deux cercles montre leur grande parenté
Le rapport du côté d'un carré sur sa diagonale met en évidence un irrationnel
(ou de l'aire d'un triangle équilatéral et du carré dans lequel il est inscrit(!))
Le rapport de l'aire d'un carré et de celui du cercle qui lui est circonscrit ... transcendance.
La difficulté que tu évoques dans la "saisie" des décimales
est de nature différente même si notre compréhension insuffisante à ce jour
du coeur de ces nombres ne nous permet pas de le percevoir comme on peut le faire pour
un nombre entier
un nombre à l'écriture décimale finie
un nombre à l'écriture décimale périodique
Merci pour ton graphique et la recherche que tu as faite
Je n'ai pas vérifié aussi loin ... et je vois grâce à tes résultats
que j'ai failli être présomptueux (sourire)²
___
Une question hors sujet
considères tu qu'il existe "une heure" qui est à la fois aujourd'hui et demain
ou que c'est seulement une façon de parler ? (minuit et 0h00)
("Cantor a tort" ?)
Lélio Lacaille - Du fagot des Nombreux
|
 |

 Accueil
Accueil
 Forum
Forum







