 |
#1 - 06-09-2022 11:22:31
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Intition 1 : coloriage
Hello ! Je me lance dans une série de problèmes sur le thème : "soit c'est faux, soit c'est hyper contre-intuitif"
Mais la démonstration n'en sera pas forcément très compliquée pour autant !
On démarre avec cet énoncé :
1. Aline trace un cercle à main levée.
2. Bernard colorie en bleu une partie de la surface de ce disque
3. Richard colorie en rouge le reste de la surface du disque
4. Zoé prétend alors pouvoir tracer une droite qui coupera le cercle en deux parties, chacune contenant autant de bleu que l'autre et autant de rouge que l'autre.
C'est vrai ou c'est faux ? (Vrai --> démonstration svp. Faux --> contre-exemple svp)
#2 - 06-09-2022 12:51:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Intutiion 1 : coloriage
Bonjour 
Pour moi c'est vrai , si on fait fait tourner un diamètre continument , on passera forcément d'un excédent bleu à un excédent rouge .
Vasimolo
#3 - 06-09-2022 17:12:37
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
intuition 1 : colorizge
Je suis d'accord, bien qu'il manque un petit quelque chose. L'énoncé précise "à main levée", ce n'est donc probablement pas un véritable cercle parfait.
#4 - 06-09-2022 17:45:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
intuition 1 : ciloriage
Oui , tu as raison mais ce n'est pas grave car on peut tourner autour de n'importe quel point . Après un demi tour on a échangé les couleurs à gauche et à droite de l'axe et comme les aires de chaque couleur varient continûment il y a aura eu un moment où elles ont été égales .
Vasimolo
#5 - 07-09-2022 00:18:20
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
ontuition 1 : coloriage
Bleu + Rouge = surface totale du cercle
Si la droite coupant le cercle de telle manière qu'on a la moitié du bleu dans une partie et la moitié dans l'autre, idem pour le rouge, existe (proposition = VRAI), cela signifie que la droite couperait le cercle pour créer une zone = 1/2 bleu + 1/2 rouge = 1/2 surface totale du cercle.
Une droite qui coupe un cercle en deux parties égales est un diamètre.
Est-ce qu'un tel diamètre existe toujours quels que soient les coloriages réalisés ?
Si mon diamètre est tel que je partage en deux la zone bleue, vu que le diamètre partage en deux le cercle complet, il partagera obligatoirement aussi la zone rouge en deux, donc il suffit de trouver un diamètre qui coupe en deux la zone bleue. Il n'est pas compliqué de se convaincre qu'en balayant tous les diamètres, on va pouvoir l'ajuster pour coupez la zone bleue en deux (et donc la zone rouge). La démonstration peut passer par le fait qu'en balayant les diamètres (un peu comme une aiguille sur une pendule qui déroule tous les angles) on peut facilement couper de manière inégale pour avoir moins que la moitié, puis pour avoir plus que la moitié, et par balayage (fonction continue) on passera nécessairement par l'égalité. Dans mes vagues souvenirs de lycée c'était un truc comme le théorème des valeurs intermédiaires ou un truc comme ça.
La réponse est donc VRAI... pour un cercle parfait.
Je ne sais pas si le fait que première phrase précise un cercle tracé à main levé requiert de ne pas considérer le cercle comme parfait ?
#6 - 07-09-2022 00:24:41
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
#7 - 07-09-2022 00:33:46
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
intuition 1 : cokoriage
Si la forme n'est pas un cercle "parfait", on oublie cette histoire de diamètre. Il suffit de prendre un point sur le pseudo cercle et de tracer la droite qui partage la forme en deux parties égales. Cette droite existe et voici comment la construire. Si la forme "presque cercle" (donc patatoide) était une plaque de métal, il suffirait de la suspendre par le point pris sur un bord et la verticale (fil à plomb) passerait par le centre de gravité de la forme et couperait donc en deux parties égales (de masses égales) la forme totale. Mathématiquement parlant, cette droite passe par le point sur le cercle et par le barycentre de la forme. On voit qu'on peut à nouveau "balayer" plusieurs cas, en faisant parcourir à un point la circonférence du pseudo cercle, on peut tracer à chaque fois la droite passant par ce point et le barycentre. Si on "balaye" toute la périphérie du cercle patatoide, on ne peut pas avoir systématiquement plus de rouge (ou de bleu) toujours du même côté, il y aura obligatoirement un point tel que le pseudo diamètre passant par ce point et le barycentre coupe la forme rouge en deux (et donc la forme bleue aussi). C'est donc VRAI aussi avec un cercle à main levée.
#8 - 07-09-2022 07:43:01
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Intuuition 1 : coloriage
Bravo Zindy. Juste deux petits détails :
1. le fil à plomb ne montre pas la verticale (d'une part à cause de la rotation de la terre, et d'autre part à cause de la déformation du géoide terrestre)
2. ça ne change rien au fait que ce que tu proposes pour la suite est parfaitement valable - mais du coup tu peux appliquer la même chose pour la première partie et arriver à la même conclusion
Question subsidiaire pas forcément plus compliquée : et si c'est pas un cercle ?
Question subsidiaire bien plus pêchue : si on passe en 3D et qu'on colorie le volume ?
#9 - 07-09-2022 12:43:27
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Intuitionn 1 : coloriage
Salut,
Puisque chacune des deux parties contient autant de bleu que l'autre et autant de rouge que l'autre, la droite séparative passe forcément par le centre du cercle.
Hormis la situation exceptionnelle où c'est un cercle concentrique qui sépare le bleu et le rouge de façon égale, ce diamètre disposé n'importe où délimitera deux zones dont l'une est plus bleue et l'autre plus rouge et on peut aussi trouver une autre position où c'est l'inverse.
Je fais maintenant tourner ce diamètre autour du centre: les proportions de bleu et de rouge varient de façon continue: je trouverai donc forcément une position du diamètre où ces proportions de bleu et de rouge sont égales.
Je réfléchis encore aux conséquences du fait que ce cercle soit tracé à main levée, et donc de façon imprécise, mais je ne vois pas trop. Je pense d'ailleurs (peut-être à tort) que cela fonctionne aussi avec un carré.
Bonne journée.
#10 - 07-09-2022 16:08:06
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Intuition 1 : coloriag
@Franky1103 : c'est tout à fait ça
#11 - 07-09-2022 23:36:27
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
Intuition 1 : coloiage
Je m'arrête à :
L'Impossibilité de tracer une droite
à moins de changer la définition
(ce qui est très courant ces temps-ci dans le domaine médical (sourire)²)
Lélio Lacaille - Du fagot des Nombreux
#12 - 08-09-2022 10:55:11
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
Intuition 1 : cooloriage
Merci Scarta pour ces précisions, je tente de répondre à tes questions subsidiaires.
Question subsidiaire pas forcément plus compliquée : et si c'est pas un cercle ?
Le principe que j'ai proposé (faire tout le "tour" de la forme en traçant à chaque fois la droite passant par le barycentre) peut se généraliser à toute forme.
Le problème serait lié à la contrainte de "couper la forme en deux parties" comme le prétend Zoé. En effet, on peut trouver des formes pour lesquelles la fameuse droite passant par le barycentre ne coupera pas la forme en deux parties mais en trois ou plus, c'est le cas de formes non convexes. Par exemple prenons un "croissant de lune" donc une forme similaire à la lettre C, si je colorie la partie haute du C en rouge et la partie basse en bleu, la droite qui pourrait couper la forme en sous ensembles avec égalité rouge/bleu coupera le croissant en trois, ce qui ne respectera pas la promesse de Zoé de "couper la forme en deux parties". Dans ce cas, on a un contre exemple, c'est FAUX
Si on en reste à l'énoncé, comme un tracé "à main levé" d'un cercle par Aline reste un cercle patatoide convexe on ne sera pas dans le cas d'une forme dont le barycentre ne ferait pas partie de la forme dessinée, c'est pour ça qu'on peut répondre VRAI à ta question d'origine. Mais FAUX à ta question subsidiaire, à cause du contre-exemple donné (le croissant de lune) qui empêche la découpe "en deux parties".
#13 - 08-09-2022 11:08:04
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
Inutition 1 : coloriage
Question subsidiaire bien plus pêchue : si on passe en 3D et qu'on colorie le volume ?
Je crois que je n'ai pas les outils mathématiques pour démontrer quoi que ce soit "proprement", mais allons y quand même sur un raisonnement. Je pense que le raisonnement précédent de couper une forme 2D type cercle en deux parties par une droite 1D doit pouvoir se généraliser à couper une forme type sphère 3D en deux parties par un plan 2D passant aussi par le barycentre, pour les mêmes raisons qu'on pourra trouver des plans coupant la sphère avec une inégalité des proportions rouges (ou bleues) dans un sens ou dans l'autre, et donc par continuité il existera le plan de coupe assurant l'égalité. Vu que la méthode utilise le barycentre, et que le concept de barycentre n'est pas limité aux formes 2D, on peut généraliser en 3D. D'ailleurs, soyons fous, je ne vois pas pourquoi le principe ne pourrait pas s'étendre, y compris bien plus loin, à couper une hypersphère 4D par une sphère 3D 
Mais je souhaite bon courage à Aline pour tracer tout ça à main levé ! 
#14 - 08-09-2022 11:33:43
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Intuition 1 : ocloriage
On parle en fait de parties mesurables au sens de Lebesgue et d'hyperplan affine. Mais c'est l'idée (et ça a été démontré, avec des gros mots comme "groupe fondamentaux" ou "homotope")
#15 - 09-09-2022 00:04:23
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
nItuition 1 : coloriage
Faut-il entendre ici que tout ce qui correspond à une action physique dans l'énoncé ou les commentaires* est à traduire en concept et en idéaux ?
Merci d'avance.
(Un peu comme pour la question "combien font 2 et 2 ..." (sourire)²)
__
* trace, main levée, colorie, pouvoir tracer, une droite, contenant
Lélio Lacaille - Du fagot des Nombreux
#16 - 09-09-2022 00:51:34
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Intuition 1 : colloriage
Tu as raison je précise donc que « tracer un cercle à main levée » ne signifie pas « lever la main gauche tout en utilisant un compas de la main droite ». Définition qui serait d’ailleurs peu inclusive pour tous les gauchers de France et de Navarre.
De toutes les façons j’ai cru comprendre que le compas n’existe pas non plus, alors pourquoi se prendre la tête ?
#17 - 09-09-2022 12:14:36
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Intuition 1 coloriage
Beaucoup de bonnes réponses, bravo !
Un peu de littérature (et de gastronomie), il existe un théorème, dit "du sandwich au jambon", qui indique (en 3 dimensions) qu'on peut couper un sandwich contenant du pain, du jambon et du gruyère en deux parties comportant chacune les même quantités pour chacun des 3 ingrédients, en un coup de couteau.
En dimension N, on parle plutôt de parties Lebesgue-mesurables et d'un hyperplan, mais bon 
C'est un théorème assez complexe : en réalité sa démonstration est plutôt courte, mais elle s'appuie sur un autre théorème, celui de Borsuk-Ulam (pas mal aussi dans le genre contre-intuitif, qui indique par exemple qu'à tout moment, il existe deux points sur la Terre aux antipodes l'un de l'autre, où la pression ET la température sont identiques), et la démonstration de ce dernier est assez corsée (lacets, homotopies, etc...)
Revenons en dimension 2: la démonstration est assez simple, elle a été bien traitée dans vos réponses, mais voici une version un peu formelle.
Pour un cercle parfait
* Je trace un diamètre quelconque, partant d'un point quelconque P du cercle
* Je calcule r(P) la différence entre les surfaces rouges dans le sens horaire et dans le sens anti-horaire. r est une fonction continue
* Au point diamétralement opposé P', j'aurai r(P') = -r(P) : les parties sont les mêmes, la soustraction est juste inversée !
* J'ai donc une fonction continue, qui admet des valeurs positives et d'autres négatives : elle admet un zéro, autrement dit un des diamètres coupera le disque de la manière demandée, avec autant de rouge de chaque côté (et donc autant de bleu, puisque ce qui n'est pas rouge est bleu et les deux demi-disques ont même surface)
Pour une forme quelconque, pareil. Il faut simplement montrer que quel que soit le point de départ qu'on prend sur une telle forme, on peut la couper en deux parties égales via une droite qui passe par ce point, et ça se fait de la même manière.
* J'ai un point de départ P
* Pour tout point P' de la forme, je peux tracer la droite (PP') qui la coupera en deux (ou sera tangente, peu importe)
* Je peux donc faire la différence entre les valeurs des surfaces de part et d'autre de cette droite, et en faire une fonction de P'
* Et puisque cette fonction est elle-aussi continue, parfois positive et parfois négative, elle admet un zéro;
On peut toujours couper cette forme en deux parties égales.
#18 - 11-09-2022 10:46:56
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 642
- Lieu: Ville 2/N près 2*i
Intuition 1 : oloriage
j'arrive un peu tard mais j'avais bien une solution, à base d'une fonction continue f(θ) du théorème des valeurs intermédiaires et d'une inversion de la couleur majoritaire entre f(θ) et f(θ+180)
#19 - 12-09-2022 18:27:56
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Intuition 11 : coloriage
J'arrive beaucoup trop tard, mais je me suis demandé ce que pouvait être un cercle dessiné à main levée.
Est-ce que cela interdit un changement de signe de la courbure quand on parcourt ce "cercle" ? En clair, peut-on admettre une forme en "haricot" telle que celle ci ?
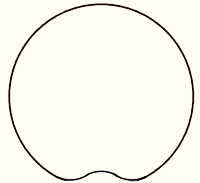
Et en exagérant la déformation, une forme telle que celle-ci ?
Spoiler : [Afficher le message] 
On peut aussi imaginer que le nombre de "tours" de cette spirale tende vers l'infini.
Question subsidiaire : Est-ce-que cela pourrait changer la réponse ta question ?
#20 - 12-09-2022 22:18:06
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Ituition 1 : coloriage
C’est mignon 🥰
Pour faire simple : ça marche quand même.
Depuis n’importe quel point tu peux couper la forme en deux parties égales. Et la fonction continue qui calcule la différence d’une couleur de part et d’autre et continue et change de signe.
Par contre… l’infini c’est beaucoup surtout vers la fin. Mais c’est vrai : quid d’une forme fractale ? Là ça devient fun.
#21 - 12-09-2022 22:58:12
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
ibtuition 1 : coloriage
Oui, avec une forme fractale ça devient fun
(l'infini) c'est très "tendance"
Lélio Lacaille - Du fagot des Nombreux
#22 - 15-09-2022 23:59:37
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
Intuitoin 1 : coloriage
Pour faire simple : ça marche quand même.
Depuis n’importe quel point tu peux couper la forme en deux parties égales. Et la fonction continue qui calcule la différence d’une couleur de part et d’autre et continue et change de signe.
C'est là que je ne suis pas tout à fait d'accord. Imaginons une forme de croissant, si elle est peinte comme ça, il existe une ligne qui coupe bien la forme en deux parties équitables avec autant de rouge et de bleu dans chaque partie
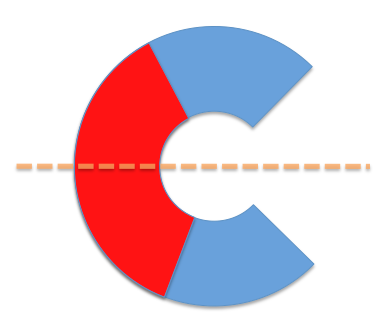
Mais on peint la forme comme suit, j'ai l'impression qu'on ne pourra pas respecter l'énoncé, il y a bien une ligne qui partage équitablement rouge / bleu, sauf qu'elle ne coupe pas la forme en deux parties mais en trois, j'ai trois "morceaux" après ma coupe. Donc oui, la droite existe, mais ne respecte pas l'énoncé de couper la forme en deux, je pense que l'énoncé ne marche qu'avec des formes convexe.

#23 - 16-09-2022 10:11:27
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
inyuition 1 : coloriage
C'est pas faux. Le fait est que ça marche quand même dans le sens "un hyperplan qui sépare les parties Lebesgue-mesurables en deux" 
#24 - 17-09-2022 01:25:58
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
Inuition 1 : coloriage
C'est pas faux. Le fait est que ça marche quand même dans le sens "un hyperplan qui sépare les parties Lebesgue-mesurables en deux" smile
Tu m'ôtes les mots de la bouche, mais n'est-on pas ici aux limites de ce que permet la caractérisation séquentielle des espaces compacts (j'entends pas là qu'on doit rester dans le domaine de la topologie des espaces métriques) via le théorème de Bolzano-Weierstrass ? Cf illustration ci-dessous
Spoiler : [Afficher le message] 
#25 - 26-12-2023 16:08:13
- stocrandy
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 1
Intuition 1 : coloriag
Puisque chacune des deux parties contient autant de bleu que l'autre et autant de rouge que l'autre, la droite séparative passe forcément par le centre du cercle.
|
 |

 Accueil
Accueil
 Forum
Forum











