Ne pas confondre le "chanfrein", découpe plane effectuée sur un angle vif, et le "congé", forme cylindrique reliant tangentiellement 2 plans .

halloduda : Le pourtour du fromage est bien sûr, tout comme le dessus et le dessous du fromage recouvert de croûte ! C'est bien là toute la difficulté du problème.
Si on revient en 2D, le problème revient alors à découper une surface en 7 parts égales et comprenant chacune une longueur égale de pourtour.

- Tous les coups de couteau donnent une découpe rectiligne (sans courbe ni angle, ce qui aurait nécessité l'utilisation de la machine à découpe par fil !) et débouchent forcément sur un bord (du fromage entier pour le 1er, ou d'un ensemble de plusieurs parts ensuite).

- Il n'est pas demandé de minimiser la longueur de découpe (c'est suffisamment compliqué ainsi). Il est juste précisé, pour avoir une solution unique et pour simplifier le problème, que le 1er coup de couteau, qui ne traverse pas forcément le fromage, est perpendiculaire à l'un des cotés.

- Il ne faut pas s'attendre à trouver des valeurs entières : toutes les valeurs obtenues appartiennent évidemment à l'ensemble des réels.

Sans congé, la découpe serait radiale "en parts de tarte", chaque part ayant une base de 360/7 mm et une hauteur de 45 mm.

Avec congé, chaque part a un côté de 49.59 mm et une aire de 1150.25 mm².



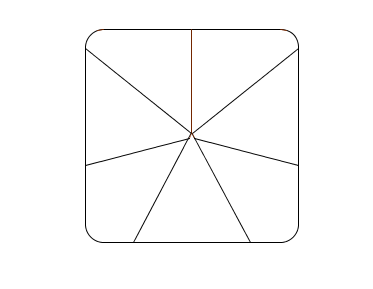
A l'échelle.

La découpe de la part du bas représente 105.2 mm

La case valide 105,2 alors qu'il est précisé
"une décimale après le point décimal".

Le logiciel gratuit Geogebra permet de trouver les cotes avec une grande précision.

Bien vu halloduda , le premier à trouver la réponse.
Et bonne continuation Franky .

Bien vu Franky pour la 1ère partie . Bon courage pour la suite .

Rques : - Le premier coup de couteau est perpendiculaire à l'un des cotés.
- La case réponse concerne la 2ème question, avec les rayons de raccordements.

Si le premier coup de couteau est perpendiculaire a un bord, il est aussi parallele a un autre. Le dernier coup de couteau peut un un symmetrique du premier, et les 4 autres coups de couteau peuvent aussi etre paralleles, mais les espaces sont differents.
Cependant:
Comme le pourtour du fromage est recouvert de croûte, la coupe depend de beaucoup de l'epaisseur du fromage, si elle n'est pas donnée, comment peut-on trouver la réponse?
Par exemple, si l'épaisseur est telle que les coupes sur les bords se font dans le congé, il y a 3 different types de parts, ce qui rend tres difficile les calculs sans connaitre l'épaisseur.

On travaille donc dans le plan et on cherche des découpes d'un septième de la longueur totale.
Je pose a le coté du carré (a=9), R le rayon des "coins" (R=0.75) et l la longueur de l'arc de cercle d'un coin.
[TeX]l=\dfrac{2{\pi}R}4[/TeX]
La longueur totale du tour est [latex]L=4(a-2R)+4l=4a-8R+4l[/latex].

On donne le premier coup de couteau est symétrique par rapport à la médiatrice de ce coté. La découpe forme donc un triangle isocèle dont le coté sur le bord du fromage mesure L/7 et la hauteur a/2.
Ce triangle se compose donc de 2 triangles rectangles dont l'hypothénuse est la découpe et les 2 autres cotés mesurent L/14 et a/2.
La longueur d'une des découpes est donc: [latex]D=\sqrt{(\dfrac{L}{14})^2+(\dfrac{a}{2})^2}[/latex].

Numériquement (on veut une précision au centième de centimètre, je travaille donc avec 6 décimales).
l=1,178097
L=34,712389 (un peu moins que 36, normal).
D=5,138

La longueur totale de la découpe fait donc 2D=10,28cm=102,8mm.
La longueur du bord fait L/7=4,96cm=49,6mm

Mais la case réponse ne valide pas

Si on appelle P l'aire de la croûte, latérale, avec un fromage de 10 cm de hauteur alors P=(324/63)*10

Bonjour,
SUITE ET FIN: seconde partie de l’énigme (la plus compliquée):
Périmètre total = 4.(90-15)+15.pi = 347,124 mm,
soit pour chacune des 7 parts = 49,589 mm
Surface totale = 90.90 – 15.15 + 7,5².pi = 7875 + 225.pi/4 = 8051,715 mm²,
soit pour chacune des 7 parts = 1150,245 mm²
La part en face du premier trait de coupe sera un triangle de base 49,589 et de hauteur 2.1150,245 / 49,589 = 46,391 mm
La longueur de coupe sera de 2.(46,391²+49,589²/4)^(1/2) = 105,2 mm (pour
103,6 pour la première partie), valeur validée par la case-réponse: OUF.
Mais je me suis juste contenté des calculs nécessaires à obtenir la réponse (je n'ai
pas calculé toutes les parts).
Bonne soirée.

Voici la découpe proposée quand le fromage n'a pas de coins arrondis :



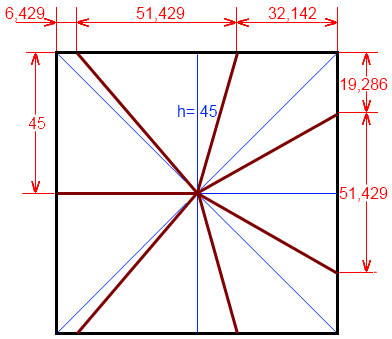
Il suffit de prendre 7 point sur le pourtour régulièrement espacés, et de les joindre au centre du carré.
Chaque portion ainsi obtenue peut être décomposée n 2 triangles de hauteur identique = 45 mm et dont la somme des bases est constante.

Vous pouvez vous inspirer de ce genre de découpe dans le cas du fromage à coins arrondis .

Bon courage !

On commence, comme pour le problème précédent, par positionner les marques de découpe sur le contour, à partir de la découpe a normale au milieu d'un coté.
Le périmètre total P fait 4*(c-2*r) + 2*pi*r soit 347.12 mm. Chaque part en contient 1/7ème soit Pp = 49.589 mm, ce qui nous donne les points A, B, B', C, C', D et D' sur le dessin :

 

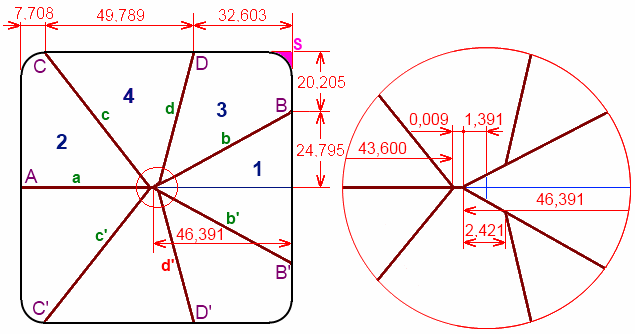
La surface de coin S est égale à  : r²*(1-pi/4) soit 6.438 mm². La surface totale à : c²-4*S soit 8051.74 mm².
Chaque part en vaut 1/7ème soit Sp = 1150.245 mm².

Déterminons le triangle 1. Sa hauteur vaut  2*Sp/Pp soit 46.391 mm (elle est supérieure à la moitié du coté).
Pythagore nous donne pour un coté de cette part, b = 52,601 mm, soit la somme des 2 bords découpés = 105.20 validé par la case réponse.

La détermination de la part 2 est un peu plus délicate. En lui ajoutant une surface de coin S, on peut la découper en 2 triangles, dont l'un connu, de base x = 7.708 et de hauteur c/2 et l'autre de base c/2 et de hauteur inconnue a.

               x*c/4 + a*c/4 = Sp+ S     on en déduit : a = 43,600 mm

La position de la découpe d se calcule ensuite à partir de la part 3 à laquelle on a rajouté la surface de coin S.
Je ne rentrerai pas dans le détail des calculs, de crainte de devenir trop fastidieux.
L'agrandissement de la partie centrale donne la forme exacte des découpes.
On remarquera qu'aucune d'entre elles ne passe par le centre du fromage.

Il est quand même très fort mon fromager !

Merci à tous ceux qui ont bien voulu se pencher sur ce petit calcul.
Un grand bravo à ceux qui sont parvenu à un résultat.