Enigme Fromage @ Prise2Tete

Ebichu · #1

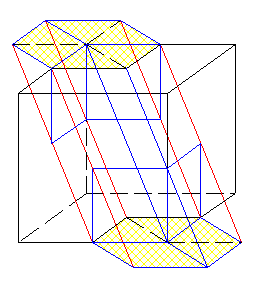
Mon fromager, agacé par une concurrence qu'il juge déloyale, a entrepris de méthodiquement détruire les apérocubes©®™ qui restent dans son réfrigérateur.

Il s'arme donc de son crayon à papier hexagonal, et l'enfonce dans l'axe de la grande diagonale d'un apérocube©™®. Par un hasard surprenant, les dimensions du crayon font que le trou formé dans l'apérocube®©™ a pour sommets les milieux des arêtes et les centres des faces de l'apérocube®™© (voir figure).

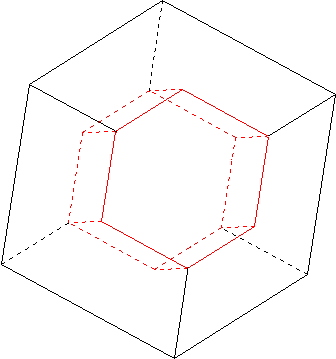
Il donne à son chien le fromage éjecté de l'apérocube™©® par le crayon, et à son chat le reste de l'apérocube™®© (la partie trouée).

Qui mangera le plus de fromage ?

(Toute ressemblance avec un certain pâtissier n'est pas fortuite, et sera l'objet de la deuxième partie de cette énigme).

dhrm77 · #2

ahhhh, question excellente....
Est-ce que l'apérocube est parfumé au poisson ou au bacon?
Peut-etre que le chat vendra sa portion au chien au lieu de la manger...

Je trouve que la partie qui reste est exactement la moitié.

w9Lyl6n · #3

Les 6 segments de la cavités parallèles à la grande diagonale sont chacuns les grandes diagonales de petits cubes de côtés 1/2

Il est alors aisé de découper en 8 cubes comme suit :

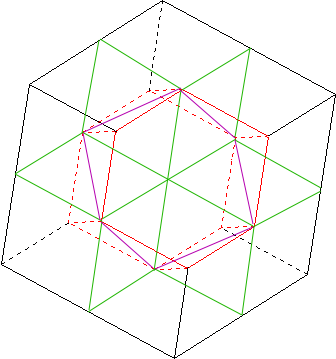
La découpe a enlevé deux petits cubes d'1/8 et six pyramides de base un côté des petits cubes, donc chacun de volume 1/24
Au totale on obtient 1/4 + 1/4 = 1/2

Le chien et le chat sont nourris a égalité

J'attends la suite

Vasimolo · #4

Bonjour,

Si on prend 4 pour arête du cube , le côté de l'hexagone régulier vaut 2 et la hauteur du prisme [latex]2\sqrt{3}[/latex] . le volume du prisme fait donc 36 , plus que 32 la moitié du cube .

Le chien a la part belle

Vasimolo

Ebichu · #5

@dhrm77 : tout à fait ! Quel est ton raisonnement ?
@w9Lyl6n : bravo ! jolie démonstration. La suite quand les 72h seront finies
@Vasimolo : non, il y a erreur, tu as vu une figure qui n'existe pas...

dhrm77 · #6

J'ai pris un cube troué de 2 de coté, coupé en 6 sections identiques, et j'ai calculé le volume d'une section qui fait donc 2/3. 6*2/3 = 4 et le cube complet fait 2x2x2=8
Donc ce qui reste est bien la moitié.
Cependant, quand j'ai voulu verifié en calculant le volume de la partie enlevée, je me suis un peu perdu dans mes calculs et je n'ai pas encore abouti.

Ebichu · #7

@dhrm77 : je pense que ton raisonnement est bon. Juste pour préciser, quelle est la forme de tes sections, et comment calcules-tu leur volume ?

dhrm77 · #8

La forme de mes sections est un prisme tronqué de chaque coté, donc un prisme moins 2 pyramides.
Le prisme fait (1*1*2)/2 =1, et chaque pyramide fait ((1*1)/2*1)/3=1/6, ce qui fait 1 - 1/6 - 1/6 = 2/3 au total.
En fait j'ai eu d'idée du découpage en regardant ton image qui est pratiquement vue dans l'axe du crayon. Divise cette vue en 6 parties égales et tu auras mes 6 sections.

La difficulté est de "voir" ces 6 sections, et de voir qu'elles suffisent a former le cube troué.

Ebichu · #9

@dhrm77 : c'est bon

enigmatus · #10

Bonjour,
La partie restante du cube est constituée de 6 volumes identiques (chacun correspondant à une face rouge). Chacun de ces volumes est constitué d'un prisme à base triangulaire et d'une pyramide.
D'après mes calculs, le chat et le chien auront des parts égales.

Franky1103 · #11

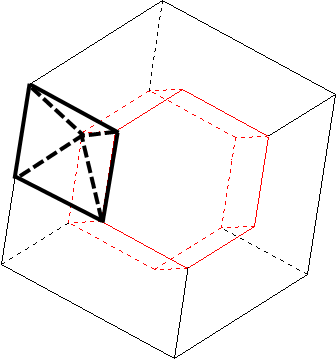
La part du chat est un objet à six arêtes de section triangulaire, dont chaque arête est composée de deux ~~tétraèdres~~ pentaèdres de base carrée (et de hauteur le côté de ce carré), soit:
V = 2 x 6 x (a/2) x (a/2)² / 3 = a³/2
La part du chat et celle du chien sont donc identiques en volume.
Merci pour cette énigme qui nécessite une bonne vision en 3D.

Edit: Complément à ma réponse
Dans la part du chat (et celle du chien), on a douze tels pentaèdres (ou symétriques) dont le sommet se trouve à la verticale d'un des quatre sommets (le carré de base étant placé horizontalement).

Ebichu · #12

@enigmatus & Franky1103 : bonnes réponses ! Il est néanmoins difficile de comprendre vos démonstrations sans un petit dessin (pour l'instant, il n'y a pas deux personnes qui aient fait le même raisonnement).

Edit : @Franky1103 : avec ton complément on comprend beaucoup mieux, merci.

Vasimolo · #13

J'ai été piégé par la perspective isométrique

Je suis trop habitué à la cavalière

Il y a sûrement plus simple mais on peut chercher la trace du crayon sur les plans des faces supérieures et inférieures du cube ( supposé d'arête 2 ) :

Le volume traversé par le crayon entre les deux plans est un prisme oblique de base 3 et de hauteur 2 donc de volume 6 . Ce qui sort du cube est constitué de quatre prismes identiques de base triangulaire d'aire 0,5 et de hauteur 1 . On a donc un trou de 6-4 X 0,5=4 , les parts sont égales .

J'attends la suite avec impatience .

Vasimolo

Ebichu · #14

@Vasimolo : parfait ! Jolie démonstration.

Ebichu · #15

Félicitations aux participants ! Tout le monde a gagné

On peut noter que la part du chien, tout comme celle du chien, peut être découpée en petites pyramides à base carrée, dont le sommet est placé à la verticale d'un des 4 sommets de la base : ce fait a été utilisé dans plusieurs des démonstrations proposées. Et c'est un problème classique que de découper un cube en 3 pyramides égales de ce type.

Je lance un nouveau fil pour la suite de cette énigme.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 16-01-2016 19:54:40

Fromaage

#0 Pub

#2 - 16-01-2016 20:36:23

Frmage

#3 - 16-01-2016 22:34:14

frpmage

#4 - 16-01-2016 22:38:45

Fromag

#5 - 16-01-2016 23:03:52

fromagr

#6 - 16-01-2016 23:10:41

dromage

#7 - 16-01-2016 23:31:19

Formage

#8 - 17-01-2016 00:13:08

Froage

#9 - 17-01-2016 00:30:40

Fromgae

#10 - 17-01-2016 07:44:45

Fromag

#11 - 17-01-2016 12:33:13

Fromge

#12 - 17-01-2016 15:13:22

Fromagge

#13 - 18-01-2016 18:21:25

Fromagee

#14 - 18-01-2016 20:01:05

Fromae

#15 - 19-01-2016 21:27:24

feomage

Réponse rapide

Sujets similaires

Pied de page des forums