 |
#1 - 22-02-2012 14:18:01
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Fromage ou dessert ?? (le retour)
J'ai rendu une nouvelle visite à mon pâtissier, mais aucun de ses gâteaux ne me tentant, je suis retourné voir mon fromager favori.
Il avait de nouveau un magnifique Brie entier (toujours parfaitement circulaire et d'épaisseur constante) sur son étal.
Me voyant arriver, il m'a tout de suite proposé de m'en couper un quart.
Je connaissais maintenant son désir d'obtenir, pour des raisons de conservation, une longueur de découpe la plus petite possible sur la partie non encore vendue, et j'étais tout fier d'avoir compris comment il faisait pour minimiser la surface sans croûte en réduisant de plus de 11 % la longueur de découpe classique .
Je pensais qu'il allait renouveler devant moi cette opération qui m'avait si impressionné la fois dernière (pour ceux qui aurait raté le premier épisode, voir :
http://www.prise2tete.fr/forum/viewtopic.php?id=10225).
Mais avec un sourire aussi énigmatique que triomphant, il se saisit du fromage, le posa sur le plateau d'une machine flambant neuve et m'annonça tout fier :
"Machine à commande numérique préprogrammé, découpe par laser au centième de mm près !"
Puis il tapota quelques chiffres sur un clavier, appuya sur un bouton et la machine se mit en route, le laser décrivant une courbe harmonieuse à la surface du Brie.
Quelques secondes plus tard, il me tendait ma portion, représentant exactement le quart du fromage.
Pourriez-vous préciser les formes et dimensions en fonction du rayon de la découpe effectuée dans ce fromage ?
Et quel est le rapport r entre la longueur de découpe et le diamètre d du fromage ? (r < 1)
Spoiler : [Afficher le message] Je n'ai pas de démonstration rigoureuse du fait que la découpe suive un arc de cercle, mais on pourra partir de cette hypothèse ici.
Spoiler : [Afficher le message] Le rayon optimum du cercle sécant est fonction de la portion de fromage enlevé :
- il tend vers l'infini et son angle d'arc tend vers 0 quand la portion tend vers 1/2 du fromage.
- il tend vers 0 et son angle d'arc tend vers pi quand la portion tend vers 0.
#2 - 22-02-2012 16:02:12
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
fromagr ou dessert ? (le retour)
Bonjour,
J'avais déjà un peu réfléchi sur ce sujet.
Soient deux cercles de même rayon R, sécants et dont la distance entre les deux centres est D.
La corde reliant les deux points d'intersection a une longueur C et l'angle sous lequel on voit cette corde depuis un centre est a.
Je suis désolé pour tout ce baratin, mais je ne sais pas dessiné sur ce site (il faudrait que j'apprenne un jour  ). ).
La surface de la lentille doit être de S = pi.R²/4, mais on a aussi:
S = 2.[aR²/2 - (D/2).(C/2)] = R².[a - 2.cos(a/2).sin(a/2)] = R².(a - sin a)
On doit donc avoir: a - sin a = pi/4, et la longueur de l'arc sera de: L = aR
Une résolution par tableur donne une longueur de coupe lenticulaire (courbe) d'env. 1,7663.R, à comparer à 2 x 0,8874.R = 1,7748.R pour une découpe rectiligne ou à 2.R pour une découpe rectiligne passant (en plus) par le centre.
Conclusion: on obtient une découpe courbe inférieure de moins de 0,5% à la découpe rectiligne (ne passant pas par le centre): je crois qu'on peut avertir ton fromager que l'investissement dans une machine numérique n'est pas vraiment rentable et qu'il est préférable qu'il continue de se servir de son bon vieux couteau.
Bonne journée à tous.
Frank
#3 - 22-02-2012 17:30:31
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
Frommage ou dessert ? (le retour)
Hello!
Je ne suis pas fan du brie mais la découpe au laser, c'est la classe pour un fromager!
Voilà la découpe qu'il a fait (me semble-t-il):
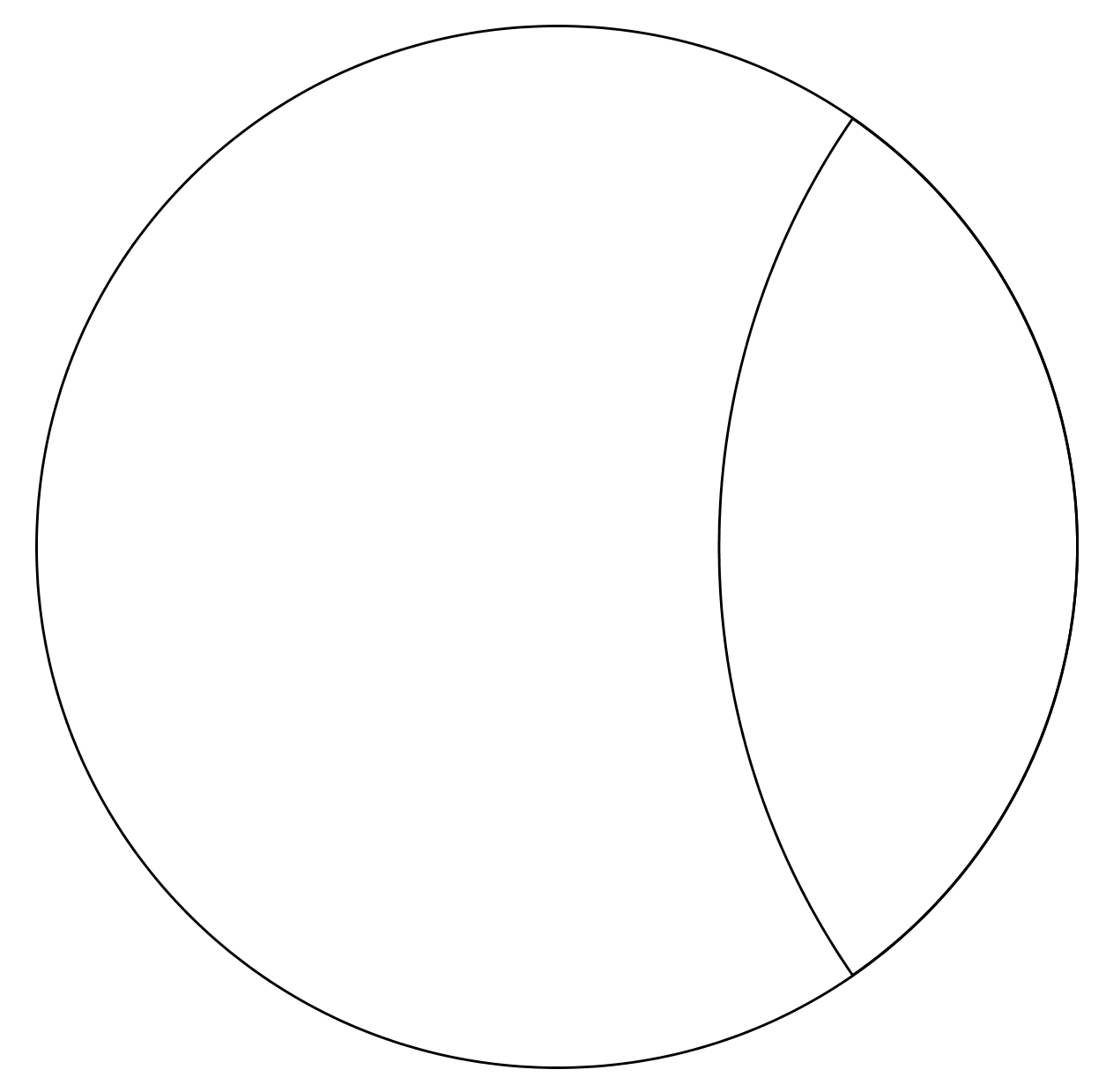
Pourquoi cette forme?
Vu de dessus, le problème revient à maximiser la surface découpée par rapport à la longueur de découpe.
Un peu d'intuition nous amène à deux choses:
- la découpe doit avoir la forme d'un arc de cercle,
- la découpe est perpendiculaire au bord du brie.
Cela revient donc à intersecter le brie avec un cercle qui coupe le bord du brie perpendiculairement.
En supposant le Brie de rayon 1, alors:
- le cercle de découpe est de rayon 1,447 ;
- la longueur de découpe est de 1,750 .
-> On obtient le quart du brie.
Ceci représente tout de même une économie de 12,5 % par rapport à une découpe classique.
Je ne comprends pas qu'on ne trouve aucune machine à découpe laser chez les fromagers.
#4 - 23-02-2012 06:20:27
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Fromge ou dessert ? (le retour)
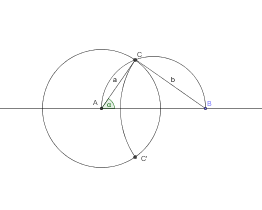
Cette fois, la découpe est un arc de cercle.
Les deux cercles sont orthogonaux, il faut résoudre l'équation :
[TeX]a² (\theta - sin\theta cos\theta) + b² (\frac{\pi } 2 - \theta - sin\theta cos\theta) =\frac{\pi a²}4[/TeX]
avec [latex]a=r,\, b=r.tg\theta[/latex]
WolframAlpha ou Geogebra permettent de dire que le rapport entre la longueur de la coupe et le diamètre est cette fois environ 0.87508...
#5 - 23-02-2012 13:29:52
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Fromage ou deessert ? (le retour)
Tu m'a pris de vitesse. J'avais deja postulé que les 2 coupes rectilignes sont des approximation d'une courbe, et que la courbe ideale serait probablement un arc de cercle ou peut-etre une hyperbole. Mais je n'ai pas eu le temps de le prouver avant de pouvoir poster une enigme similaire. Le tout est de trouver:
- s'il s'agit effectivement d'un arc de cercle,
- comment trouver le diametre et centre de ce nouveau cercle (je postule ici qu'au points d'intersection les 2 arcs de cercles forment un angle droit)
Je ferais donc un calcul en supposant qu'il s'agit d'un arc de cercle, mais j'aimerais savoir si tu as pu le prouver (a la fin de l'énigme, bien entendu)
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#6 - 23-02-2012 13:39:35
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
ftomage ou dessert ? (le retour)
Pas certain de bien comprendre, donc je biaise un peu.
Un laser n'ayant pas les même contrainte de découpe qu'un couteau, je propose un cercle de rayon R/2. (quoi de plus harmonieux qu'un cercle?)
On a donc L/D=pi/2
En fait, j'ai l'impression que la solution est arbitraire.
#7 - 23-02-2012 16:58:07
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Fromage ou dessert ? (le rtour)
#8 - 23-02-2012 17:30:08
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
FFromage ou dessert ? (le retour)
Je parle d'un disque de brie prélevé dans le brie. Je me doute que ce n'est pas la réponse attendue, mais je trouve ça harmonieux. Comme en plus ton énoncé ne mentionne pas qu'on cherche à minimiser la découpe...
Bref, c'était juste pour participer.
#9 - 23-02-2012 23:50:03
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Fromage ou desesrt ? (le retour)
@Jackv
Pourquoi deux cercles de même rayon ? Sans savoir le démontrer de façon rigoureuse, je pense que cette situation correspond à un optimum, à l'image d'un cercle (maximisant le rapport surface / périmètre) ou d'une sphère (pour le rapport volume / surface).
J'ai essayé de reprendre mes équations avec deux cercles de rayons différents, mais les calculs deviennent rapidement imbuvables.
Bonne soirée.
#10 - 24-02-2012 04:54:15
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Fromage ou desssert ? (le retour)
En supposant que la solution est un arc de cercle.
J'appelle A et B les point d'intersection de l'arc de cercle avec la peripherie du fromage.
Si l'angle AOB est inferieur a 120 degres (ou la portion a decouper est inferieure a 27.57%)
alors, le centre de ce nouvel arc est placé a la peripherie du fromage.
Sinon, c'est le centre du fromage qui est a la périphérie de l'arc de cercle de decoupe.
Pour 1/4 du fromage (si je n'ai pas fait d'erreurs, ce dont je doute fortement pour l'instant)
Le rayon de ce cercle serait de 0.7747529*18 soit 13.945553 ce qui me semble un peu trop court
l'angle AOB serait de 91.1654164 degres
X etant le centre de l'arc de cercle,
l'angle AXB serait de 134.4171918 degres.
mais comme je pense avoir une erreur, je reviendrais.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#11 - 24-02-2012 22:30:19
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Fomage ou dessert ? (le retour)
racine, Franky, dhrm : non, ce n'est pas la réponse attendue  ... ...
#12 - 25-02-2012 12:47:43
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Froomage ou dessert ? (le retour)
En fait j'avais (presque) bon la premiere fois, c'était ma reference a 60 degrés qui était fausse.
Je trouve un rapport r entre la longueur de découpe et le diamètre d du fromage de 0.908795 soit 90.8795%
wait...
c'est pire que la decoupe avec 2 coups de couteau qui a un rapport de 0.8874383
La supposition que le centre de l'arc de cercle se trouve sur la périphérie du fromage doit donc etre fausse.
Je corrige:
Donc si on suppose que le centre de l'arc de cercle est a l'exterieur du fromage, je trouve:
- un rayon de cet arc de cercle de 1.4474173 fois le rayon du fromage
- un distance entre les 2 centres de 1.7592716 fois le rayon du fromage.
- un raport r entre la longueur de découpe et le diamètre d du fromage de 0.8750804 soit 87.50804%
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#13 - 25-02-2012 16:06:42
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
fromagz ou dessert ? (le retour)
dhrm : cette fois ci, on est parfaitement d'accord  ! !
#14 - 25-02-2012 16:52:42
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Fromage ou dessert ? (le retouur)
En solution générale, je pense que le centre de l'arc de cercle se trouve ou les 2 tangentes au points d'intersection des 2 cercles se rejoignent.
Donc pour une part de 0%, ce centre se trouve sur la périphérie du fromage, et en augmentant la part a decouper vers les 50%, le centre s'éloigne progressivement du fromage vers l'infini. et le rayon de cet arc de cercle tend aussi vers l'infini.
Et donc il n'y a pas de cas spécial a 120 degrés (ou 27.57% du fromage) comme je l'avais supposé auparavant.
Ca marche maintenant avec tous les cas que j'ai éssayé.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#15 - 26-02-2012 13:46:01
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Froage ou dessert ? (le retour)
- La forme optimale de découpe est en arc de cercle.
N'étant pas prof de math, je vais quand même en tenter une simili-démonstration par l'absurde, qui ne convaincra certainement pas les puristes.
Supposons que ce soit un autre type de courbe, par exemple un arc de parabole ou d'ellipse (courbe rouge).
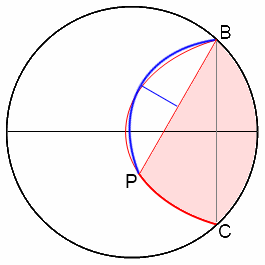
Si je j'impose un pourtour fixe du point C jusqu'à un point quelconque P de cette courbe, la nouvelle courbe optimisant le reste de la découpe pour la même surface devra être du même type que la précédente et superposée à celle-ci (arc bleu). La seule solution est que courbure soit constante en tout point de la découpe, ce qui correspond au cas de l'arc de cercle (ou du segment de droite qui peut être considéré comme un arc de cercle dégénéré à courbure nulle).
- La découpe est normale au cercle aux points d'intersection.
Ma démonstration risquant d'être encore plus sujette à caution, je laisse aux spécialistes le soin de prouver la validité de cet axiome  . .
- Comment varie le rayon de cette découpe ?
Il part de 0 et tend vers l'infini lorsque la proportion de fromage désirée passe de 0 à 1/2, puis retourne à 0 quand la proportion devient égale à 1.
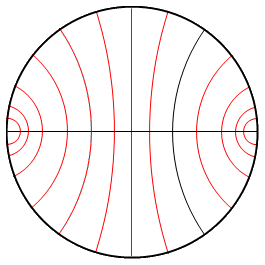
Par rapport à la découpe classique , le gain de longueur passe dans le même temps de 100 % à 0 %, pour revenir à 100%.
On peut bien sûr obtenir la proportion souhaitée sur un fromage ainsi entamé, avec pour seul inconvénient le fait que pour une nouvelle proportion faible, la part de fromage devient alors très difficile à manipuler  ! !
- Que vaut le rapport "longueur de découpe / diamètre du fromage" pour une part égale au quart du fromage. ?
On choisit comme unité de mesure le rayon r du fromage.
L'aire de l'onglet BAC est égale à l'aire du secteur OCOB moins l'aire du triangle OBC.
Il a comme valeur [latex]\alpha-\sin(\alpha)*\cos(\alpha)[/latex].
Le secteur O'BO'C a un angle [latex]\beta=\pi/2-\alpha[/latex] et un rayon [latex]R = r*\tan(\alpha)[/latex] .
Comme [latex]\cos(\beta)=\sin(\alpha)[/latex] et [latex]\sin(\beta)=\cos(\alpha)[/latex] , l'aire de l'onglet BA'C a donc comme valeur :
[latex]\tan²(\alpha)*[(\pi-\alpha)-\sin(\alpha)*\cos(\alpha)][/latex].
On souhaite que la somme de ces 2 onglets ait une aire égale à [latex]\pi/4[/latex].
N'étant toujours pas adepte de Wolfram Alpha, je me contente d'utiliser un tableur.
J'obtiens l'égalité des aires pour [latex]\alpha[/latex] = 55.3595 ° = 0.966206 rd.
Avec ces valeurs, on obtient R= 1.447394 *r
et un rapport "longueur de découpe / diamètre du fromage" de :
0.87508042
Cela nous donne un gain de 12,5 % par rapport à la découpe classique, mais seulement 1,25 % par rapport à la découpe au couteau optimisée  ... ...
On peut se demander si il était rentable d'investir dans une machine de découpe laser à commande numérique ... Mais heureusement, une telle machine peut être utilisée à d'autres fins qu'à la découpe optimisée, même par un fromager  ! !
Merci à tous ceux qui ont participé  , bravo à ceux qui ont trouvé la solution , bravo à ceux qui ont trouvé la solution  . .
Et à bientôt pour de nouvelles aventures fromagères  . .
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum











