 |
#1 - 06-05-2012 23:06:31
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
fromage ou desseet ? 4
On organise une cousinade et je me suis tout de suite proposé pour m'occuper, non pas du dessert, mais plutôt du fromage  . .
Je suis donc aller mon fromager préféré et lui ai commandé pour la date fixée un Brie de Meaux (vous savez, ce magnifique fromage de 2.8 kg pour 36 cm de diamètre) découpé en 72 parts, bien évidemment égales.
Plutôt que faire converger toutes les parts au centre avec un angle trop faible pour une bonne tenue de la part, il m'a alors proposé de réaliser la découpe avec un cercle intermédiaire, selon le principe de ce schéma :
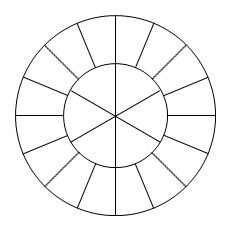
Il précisa aussitôt qu'il se servirait de sa "fabuleuse" machine de découpe Laser à commande numérique afin, bien évidemment, de minimiser la longueur de découpe.
Combien de parts devraient comporter le disque central et l'anneau périphérique ?
Quel serait le diamètre de la découpe intermédiaire et la longueur de découpe obtenue ?
#2 - 06-05-2012 23:52:33
- Moriss
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 460
dromage ou dessert ? 4
Jackv a écrit:Combien de parts devraient comporter le disque central et l'anneau périphérique ?
Quel serait le diamètre de la découpe intermédiaire ?
Ces deux questions me semblent ne pas pouvoir cohabiter :
1) Si on se demande combien de parts faire, alors l'énoncé doit fixer le diamètre de la découpe intermédiaire :
Par exemple à 1/2 du diamètre du fromage :
Dans cet exemple, le cercle intérieur fait le quart du fromage. Il doit donc comporter le quart des parts soit 18 parts dans le cercle intérieur, les 3/4 des parts restantes étant découpées dans l'anneau extérieur (54 parts, trois fois plus que dans le cercle intérieur).
2) Si on se demande quel diamètre doit faire la découpe intermédiaire, alors l'énoncé doit fixer le nombre de parts dans le disque central.
Par exemple, en s'appuyant sur le schéma présenté, il y a deux fois moins de parts au centre qu'à la périphérie, soit 24 parts au centre :
Dans cet exemple, le cercle intérieur doit être le 1/3 du fromage, son diamètre doit donc être celui du fromage divisé par racine de 3.
d = D / V3 = D . 0,57735 environ.
#3 - 07-05-2012 09:27:28
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Fromage ou dssert ? 4
Bonjour,
Soient R le rayon du fromage et kR (avec 0 < k < 1) celui du disque central.
Soient N le nombre de parts du disque central et pN (p entier) celui de l'anneau.
On a la relation: pi.(R²-k²R²) = p.pi.k²R², simplifié en: p = 1/k² - 1.
De plus: N.(p+1) = 72 donne: N = 72.k².
La découpe est de: D = 2.pi.kR + N.kR + pN.(R-kR),
soit: D/R = 2.pi.k + 72.k³ - 72.k² / (k+1).
On cherche à optimiser D/R par rapport à k.
Donc: d(D/R)/dk = 0, ce qui donne:
2.pi + 216.k² - 72.[2k(k+1) - k²] / (k+1)² = 0,
soit: (pi+108.k²)(k+1)² - 36(k²+1) = 0.
Je me retrouve avec une équation du 4è degré en k sans solution évidente (et il est tard): je vais faire appel à un tableur et je trouve k= env. 0,408603.
On en déduit N = 12 et p = 5.
Le disque central comporte donc 12 parts et l'anneau périphérique 5 x 12 = 60 parts.
La découpe intermédiaire a un diamètre de 2.kR = env. 29,4 cm.
Bonne journée.
#4 - 07-05-2012 11:03:19
- Christian91
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 89
- Lieu: 91
Fromage ou dessert ?4
8 parts du disque central
64 parts dans l'anneau
diamètre du disque central 12 cm
#5 - 07-05-2012 11:50:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
fromage ou sessert ? 4
Je trouve que la découpe minimale est obtenue lorsque le rayon du cercle intérieur est 0.59081..fois le rayon du cercle extérieur. On a alors un partage de 25 parts à l'intérieur et 47 parts à l'extérieur. Mais comme le partage ne tombe pas juste, il faut réajuster le rapport à rac(25/72)=0.5892...Ce qui donne un rayon de 15/rac2 rapporté à notre problème.
#6 - 07-05-2012 12:02:32
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
#7 - 07-05-2012 22:21:35
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Frommage ou dessert ? 4
Rebonjour,
Il n'y a pas de soucis pour revoir ma copie que voici (j'ai aussi laissé l'ancienne).
Soient R le rayon du fromage et kR (avec 0 < k < 1) celui du disque central.
Soient N le nombre de parts du disque central et M celui de l'anneau périphérique.
On a la relation: N.pi.(R²-k²R²) = M.pi.k²R², simplifié en: M/N = 1/k² - 1.
De plus: N+M = 72 donne: N = 72.k² et M = 72.(1-k²).
La découpe est de: D = 2.pi.kR + N.kR + M.(R-kR),
soit: D/R = 2.pi.k + 72.k³ + 72.(1-k²)(1-k),
ou encore: D/R = 2.pi.k + 72.(2k³ - k² - k + 1).
On cherche à optimiser D/R par rapport à k.
Donc: d(D/R)/dk = 0, ce qui donne: 2.pi + 72.(6k² - 2k - 1) = 0.
Je me retrouve avec une équation du 2è degré en k sans solution évidente : je vais faire appel à un tableur et je trouve k= env. 0,590813, d'où N = 25 et M = 47.
Le disque central comporte donc 25 parts et l'anneau périphérique 47 parts.
La découpe intermédiaire a un diamètre de 2.kR = env. 21,27 cm.
Bonne journée.
#8 - 07-05-2012 22:37:47
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
#9 - 08-05-2012 02:12:19
- Moriss
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 460
#10 - 08-05-2012 10:01:45
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
fromage ou desdert ? 4
Réponse complète et précise de Moriss  
#11 - 08-05-2012 14:07:03
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1015
Formage ou dessert ? 4
Après avoir essayé des découpes sur une douzaine de fromages, nous sommes arrivés à ce résultat:
Le disque central comporte 25 parts.
L'anneau périphérique comporte 47 parts.
Le diamètre de la découpe du cercle intermédiaire est approximativement de 21,21320344 cm.
Nous avons une longueur totale de découpe d'environ 679,2980063 cm.
Les lutins ayant procédé au découpage du fromage gagnant ont ensuite réalisé un graphique avec un tableur pour nous prouver qu'ils ne pouvaient pas faire mieux:
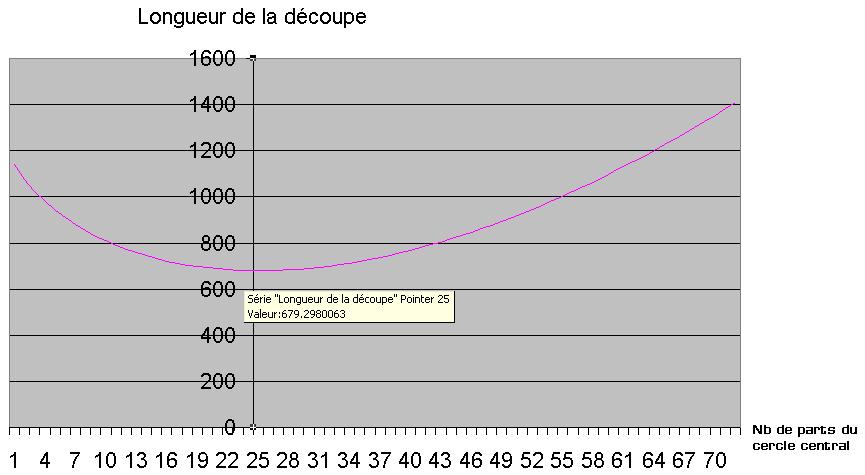
La prochaine fois, je leur suggérerai d'utiliser le tableur d'abord, et d'acheter le fromage ensuite. 
#12 - 08-05-2012 22:53:28
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Fromage ou dessert ?
Une autre réponse complète et très précise d'elpafio   ! !
#13 - 09-05-2012 19:08:39
- ThomasLRG
- Habitué de Prise2Tete
- Enigmes résolues : 41
- Messages : 31
Fromage ou dessertt ? 4
L'aire totale du fromage est de [latex]18^2 \pi[/latex] donc l'aire d'une part est de [latex]\frac{18^2 \pi}{72} = \frac{9}{2}\pi[/latex]
Soit 0<n<72 le nombre de part dans la partie centrale. L'aire du disque central est donc de [latex]\frac{9n}{2} \pi}[/latex]. Donc le rayon du disque central est de [latex]\sqrt{\frac{9n}{2}}=\frac{3\sqrt{2 n}}{2}[/latex]
Pour 1 < n < 71, la longueur de la découpe comprend :
la découpe du disque central : [latex]2 \pi \frac{3\sqrt{2 n}}{2} = 3\sqrt{2 n} \pi[/latex]
les n rayons délimitants les n parts au centre : [latex]n \frac{3\sqrt{2 n}}{2}[/latex]
les n parties de rayons délimitants les 72 - n parts de la couronne : [latex](72-n)(18-\frac{3\sqrt{2 n}}{2})[/latex]
On étudie alors la fonction f qui à x associe la somme de ces 3 termes et on trouve un minimum pour [latex] x \simeq 25,1 [/latex]
Finalement f(25) < f(26), donc 25 parts centrales donnent une longueur minimale à la découpe pour un nombre de part compris strictement entre 1 et 71.
Reste a calculer les 2 cas spéciaux n = 1 et n = 72 (pas de découpe au centre pour l'un, et pas de découpe sur la couronne pour l'autre), mais aucun ne fait mieux que n = 25.
Conclusion : Pour minimiser la découpe, on obtient 25 parts centrales, 47 parts sur la couronne.
le diamètre du cercle intermédiaire est d'environ 21 cm
Et la longueur finale est d'environ 679.3 cm
#14 - 09-05-2012 19:44:50
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Formage ou dessert ? 4
Bienvenue Thomas dans notre cercle de fous  ! !
Pour une première participation au forum, c'est un plein succès.
Ce sont les bons nombres de parts. Bravo  et à bientôt. et à bientôt.
#15 - 10-05-2012 03:44:29
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Fromage ou desesrt ? 4
25 parts a l'interieur, 47 a l'exterieur,
pour une coupe minimale de 679.298006
le rayon du cercle interieur est de 10.606602
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#16 - 10-05-2012 09:31:08
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
fromage ou dessery ? 4
Bravo à dhrm  pour une réponse complète, à la fois très concise et précise. pour une réponse complète, à la fois très concise et précise.
#17 - 11-05-2012 10:08:15
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
fromage ou desqert ? 4
J'ai moi aussi utilisé un tableur pour arrivé au bout de ce petit problème.
Soient re le rayon extérieur du fromage, r celui de la découpe circulaire, N1 le nombre de parts dans le cercle central, N2 (= 72 - N1) celui dans l'anneau.
Le rayon de la découpe intermédiaire est tout simplement r = re * rac (N1/72).
La longueur totale de découpe est la somme de la circonférence 2 pi*r, des N1 découpes de longueur r et des N2 découpes de longueur (re - r).
Il ne reste plus qu'à faire varier le nombre de parts N1 pour voir comment évolue cette longueur totale.
On trouve effectivement un minimum pour N1 = 25, N2 = 47 avec r = 106.066 mm et une longueur de découpe = 6792.88 mm.
Encore bravo  à nodgim, Francky, Moriss, elpafio, thomas et dhrm pour avoir résolu cette petite énigme. à nodgim, Francky, Moriss, elpafio, thomas et dhrm pour avoir résolu cette petite énigme.
Il ne me reste plus qu'à retourner prendre ma commande dûment découpée dans une quinzaine de jours pour la déguster en compagnie de toute la famille réunie. (à suivre...)
#18 - 11-05-2012 18:06:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Fromage ou desserrt ? 4
Euh...ça se fait sans tableur bien sûr.
Le fait que toutes les parts sont égales conduit à l'écriture d'une équation de degré 3. La dérivée est une fonction de degré 2 à parabole dirigée vers le haut, donc il suffit de trouver la racine positive pour trouver la valeur min de découpe.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







